Here’s batch 2 of my old google+ posts on ‘Inter Universal Teichmuller theory’, or rather on the number theoretic examples of Frobenioids.
June 5th, 2013
Mochizuki’s categorical prime number sieve
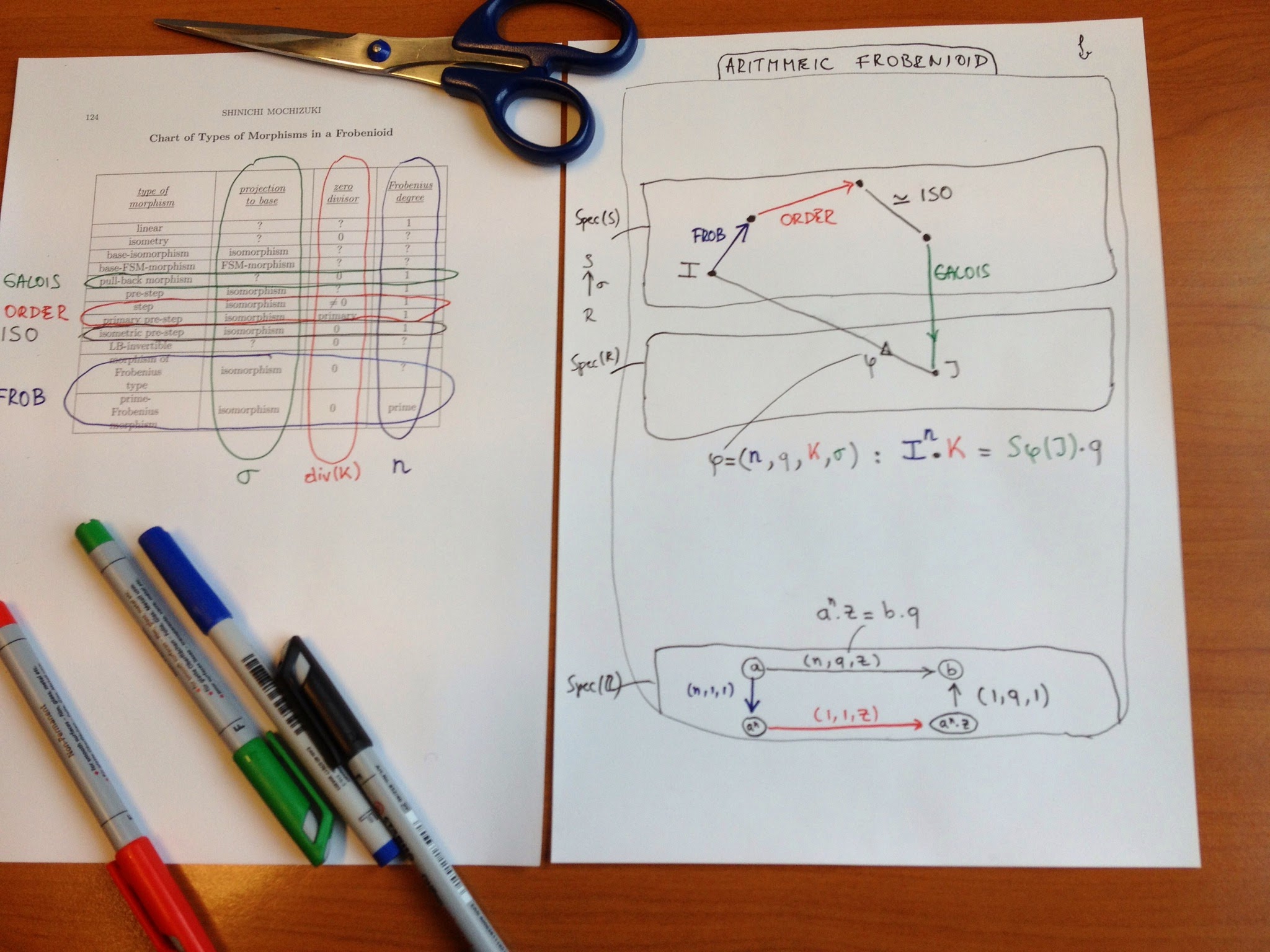
And now for the interesting part of Frobenioids1: after replacing a bunch of arithmetic schemes and maps between them by a huge category, we will reconstruct this classical picture by purely categorical means.
Let’s start with the simplest case, that of the ‘baby arithmetic Frobenioid’ dismantling $\mathbf{Spec}(\mathbb{Z}) (that is, the collection of all prime numbers) and replacing it by the category having as its objects
all $(a)$ where $a$ is a strictly positive rational number
and morphisms labeled by triples $(n,r,z)$ where $n$ and $z$ are strictly positive integers and $r$ is a strictly positive rational number and connecting two objects
\[
(n,r,z) : (a) \rightarrow (b) \quad \text{ if and only if } \quad a^n.z=b.r \]
Composition of morphisms is well-defined and looks like $(m,s,v) \circ (n,r,u) = (m.n,r^m.s,u^m.v)$ as one quickly checks.
The challenge is to recover all prime numbers back from this ‘Frobenioid’. We would like to take an object $(a)$ and consider the maps $(1,1,p)$ from it for all prime numbers $p$, but cannot do this as categorically we have to drop all labels of objects and arrows. That is, we have to recognize the map $(1,1,p)$ among all maps starting from a given object.
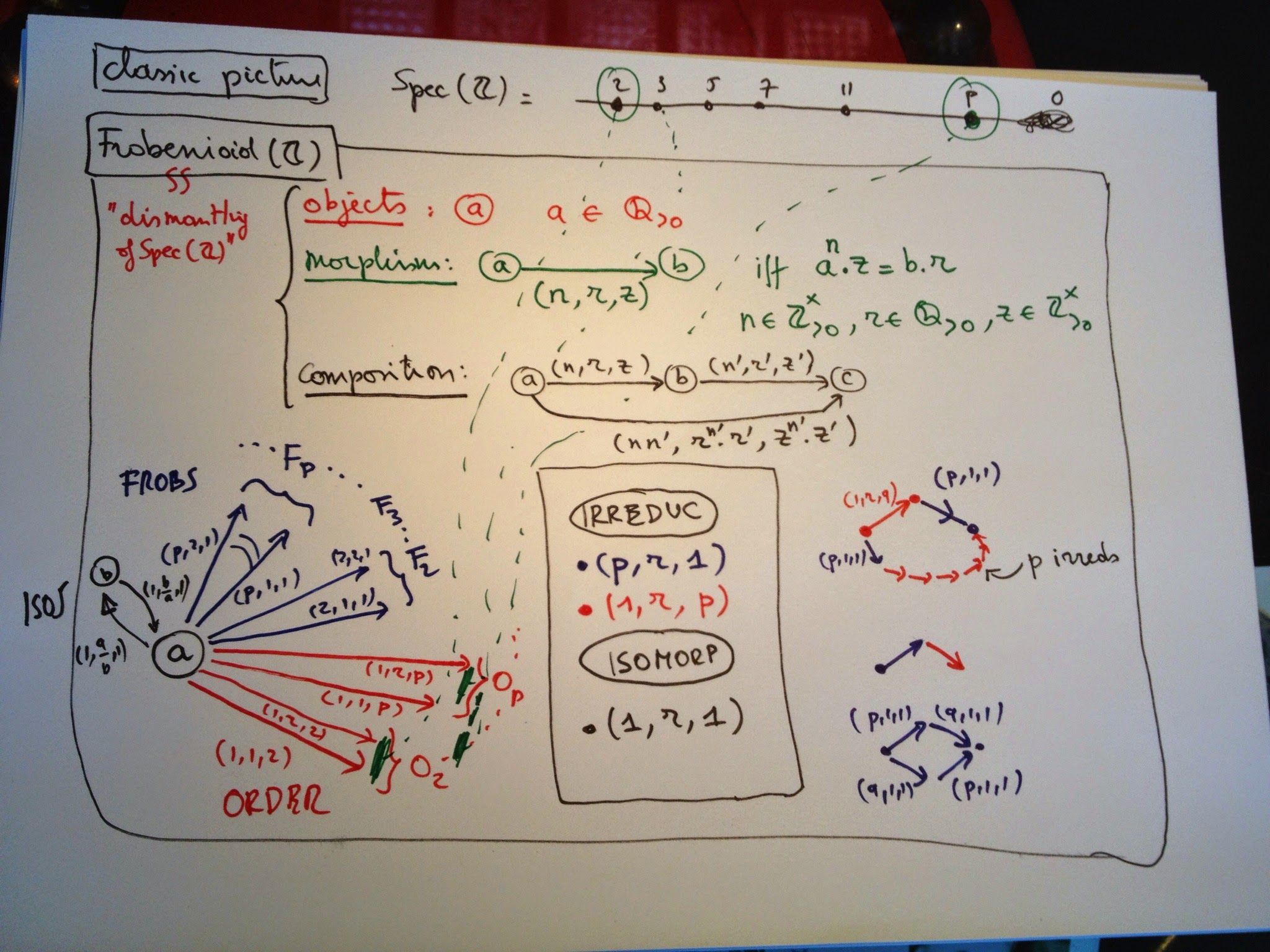
We can identify all isomorphisms in the category and check that they are precisely the morphisms labeled $(1,r,1)$. In particular, this implies that all objects are isomorphic and that there is a natural correspondence between arrows leaving $(a)$ and arrows leaving $(b)$ by composing them with the iso $(1,b/a,1) : (b) \rightarrow (a)$.
Another class of arrows we can spot categorically are the ‘irreducibles’, which are maps $f$ which are not isos but have the property that in any factorization $f=g \circ h$ either $g$ or $h$ must be an iso. One easily verifies from the composition rule that these come in two flavours:
– those of Frobenius type : $(p,r,1)$ for any prime number $p$
– those of Order type : $(1,r,p)$ for any prime number $p$
We would like to color the froBs Blue and the oRders Red, but there seems to be no way to differentiate between the two classes by purely categorical means, until you spot Mochizuki’s clever little trick.
start with a Red say $(1,r,q)$ for a prime number $q$ and compose it with the Blue $(p,1,1)$, then you get the morphism $(p,r^p,q^p)$ which you can factor as a composition of $p+1$ irreducibles
\[
(p,r^p,q^p) = (1,r,q) \circ (1,r,q) \circ …. \circ (1,r,q)o(p,1,1) \]
and if $p$ grows, so will the number of factors in this composition.
On the other hand, if you start with a Blue and compose it with either a Red or a Blue irreducible, the obtained map cannot be factored in more irreducibles.
Thus, we can identify the Order-type morphisms as those irreducibles $f$ for which there exists an irreducible $g$ such that the composition $g \circ f$ can be factored as the composition in at least $n$ irreducibles, where we can take n arbitrarily large.
Finally we say that two Reds out of $(a)$ are equivalent iff one is obtained from the other by composing with an isomorphism and it is clear that the equivalence classes are exactly the arrows labeled $(1,r,p)$ for fixed prime number $p$.
So we do indeed recover all prime numbers from the category.
Similarly, we can see that equivalence classes of Frobs from $(a)$ are of the form $(p,r,1)$ for fixed prime $p$. An amusing fact is that we can recover the prime $p$ for a Frob by purely categorical ways using the above long factorization of a composition with a Red.
There seems to be no categorical way to determine the prime number associated to an equivalence class of Order-morphisms though… Or, am i missing something trivial?
June 7th, 2013
Mochizuki’s Frobenioids for the Working Category Theorist
Many of you, including +David Roberts +Charles Wells +John Baez (and possibly others, i didn’t look at all comments left on all reshares of the past 4 posts in this MinuteMochizuki project) hoped that there might be a more elegant category theoretic description of Frobenioids, the buzz-word apparently being ‘Grothendieck fibration’ …
Hence this attempt to deconstruct Frobenioids. Two caveats though:
– i am not a category theorist (the few who know me IRL are by now ROFL)
– these categories are meant to include all arithmetic information of number fields, which is a messy business, so one should only expect clear cut fibrations in easy situation such as principal ideal domains (think of the integers $\mathbb{Z}$).
Okay, we will try to construct the Frobenioid associated to a number field $K$ (that is, a finite dimensional extension of the rationals $\mathbb{Q}$) with ring of integers $R$ (the integral closure of $\mathbb{Z}$ in $K$). For a concrete situation, look at the quadratic case.
The objects will be fractional ideals of K which are just the R-submodules $I$ of $K$ such that there in an $r$ in $R$ such that $I.r$ is a proper ideal of $R$. Dedekind showed that any such thing can be written uniquely as a product
\[
I = P_1^{a_1} … P_k^{a_k} \]
where the $P_i$ are prime ideals of $R$ and the $a_i$ are integers (if they are all natural numbers, I will be a proper ideal of $R$). Clearly, if one multiplies two fractional ideals $I$ and $J$, the result $I.J$ is again a fractional ideal, so they form a group and by Dedekind’s trick this group is the free Abelian group on all prime ideals of $R$.
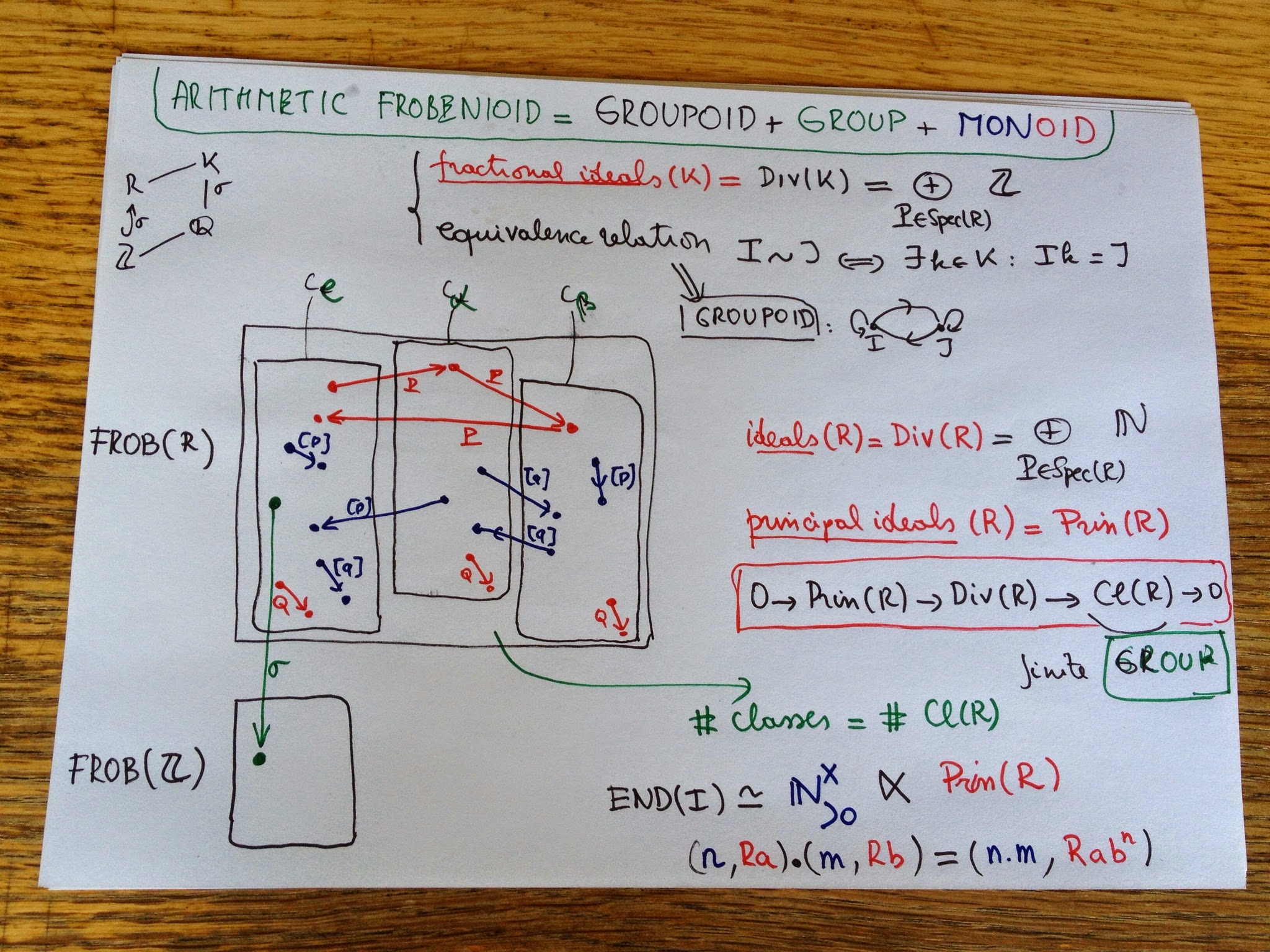
Next, we define an equivalence relation on this set, calling two fractional ideals $I$ and $J$ equivalent if there is a $k$ in $K$ such that $I=J.k$ (or if you prefer, if they are isomorphic as $R$-modules).
We have a set with an equivalence relation and hence a groupoid where these is a unique isomorphism between any two equivalent objects. This groupoid is precisely the groupoid of isomorphisms of the Frobenioid we’re after.
The number of equivalence classes is finite and these classes correspond to the element of a finite group $Cl(R)$ called the class group of $R$ which is the quotient group of ideals modulo principal ideals (so if your $R$ is a principal ideal domain there is just one component). The ‘groups’ corresponding to each connected component of the groupoid are all isomorphic to the quotient group of the units in $K$ by the units in $R$.
Next, we will add the other morphisms. By definition they are all compositions of irreducibles which come in 2 flavours:
– the order-morphisms $P$ for any prime ideal $P$ of $R$ sending $I$ to $I.P$. Typically, these maps switch between different equivalence classes (unless $P$ itself is principal). We can even explicitly compute small norm prime ideals which will generate all elements in the class group $Cl(R)$.
– the power-maps $[p]$ for any prime number $p$ which sends $I$ to $I^p$. The nature of these maps really depend on the order of the component in the finite group $Cl(R)$.
Well, that’s it basically for the layer of the Frobenioid corresponding to the number field $K$. (You have to repeat all this for any subfield between $\mathbb{Q}$ and $K$). A cute fact is that all endomorphism-monoids of objects in the layer of K are all isomorphic as abstract monoid to the skew-monoid
$\mathbb{N}^x_{>0} x Prin(R)$ of the multiplicative group of all strictly positive integers $n$ with the monoid of all principal ideals in R with multiplication defined by
\[
(n,Ra).(m,Rb)=(nm,Rab^n) \]
The only extra-type morphisms we still have to include are those between the different layers of the Frobenioid, the green ones which M calls the pull-back morphisms.
They are of the following form: if $R_1$ and $R_2$ are rings of integers in the fields $K_1$ contained in $K_2$, then for any ringmorphism $\sigma : R_1 \rightarrow R_2$ one can extend a fractional ideal $I$ of $R_1$ to $K_2$ by considering $R_2.\sigma(I)$. These then give the morphism $r_2\sigma(I) \rightarrow I$ and as we will see in a next instalment, they encode the splitting behaviour of prime ideals.
a question for category people
Take the simplest situation, that of the integers $\mathbb{Z}$. So, we have just a groupoid with extra morphisms generated by the order-maps $o_p$ and the power maps $f_p$. The endo-ring of any object is then isomorphic top the abstract group generated by the $f_p$ and $o_p$ and satisfying following relations
\[
o_p.o_q=o_q.o_p \]
\[
f_p.f_q=f_q.f_p \]
\[
f_p.o_q=o_q^p.f_p \]
My question now is: if for two different primes $p$ and $q$ i switch their role in the endo-ring of 1 object and propagate this via all isos to all morphisms, do i get a category equivalence? (or am i missing something?). (tbc)
June 11th, 2013
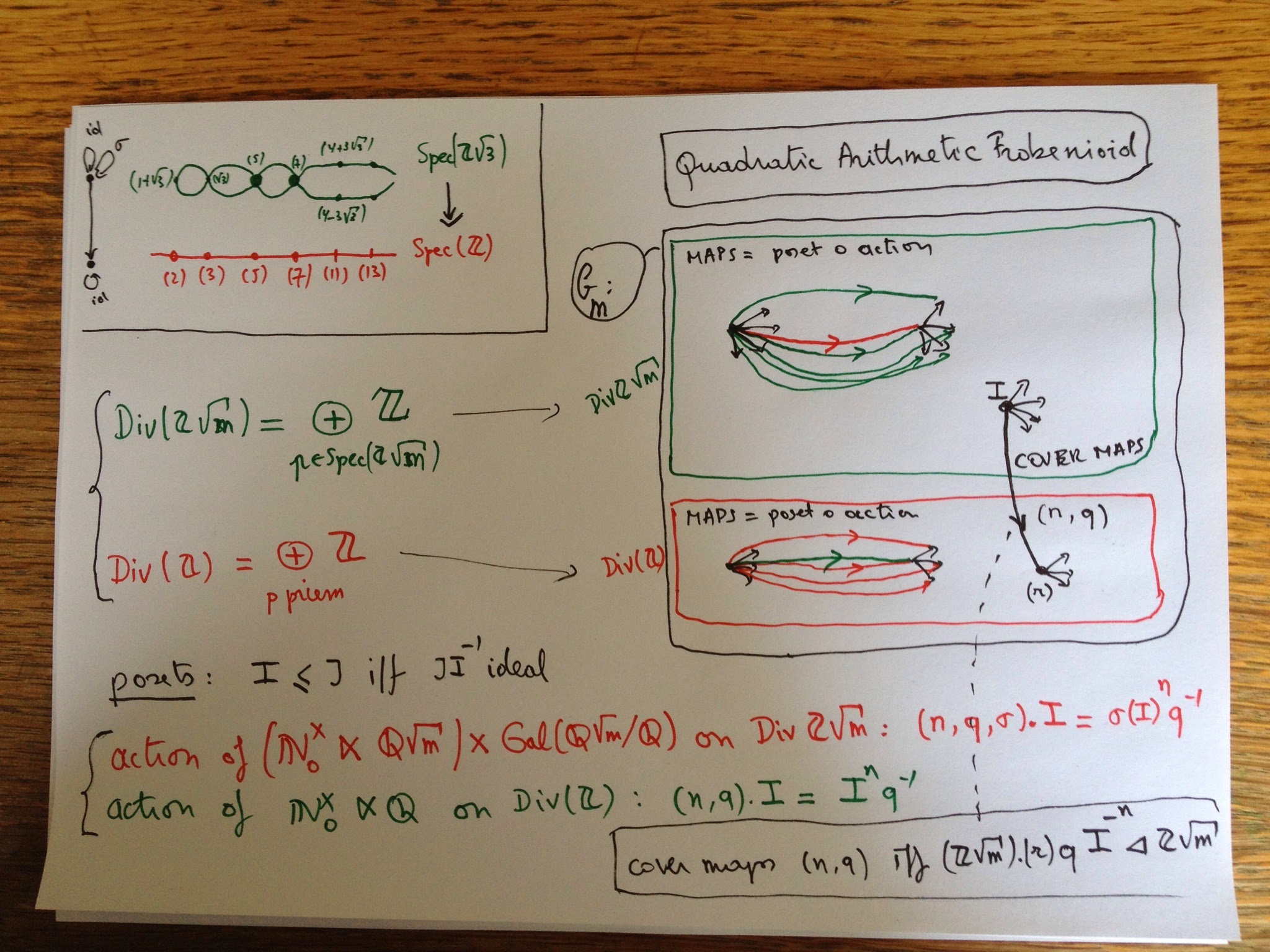
my problem with Mochizuki’s Frobenioid1
Let us see how much arithmetic information can be reconstructed from an arithmetic Frobenioids. Recall that for a fixed finite Galois extension $L$ of $\mathbb{Q}$ this is a category with objects all fractional ideals in subfields of $L$, and maps generated by multiplication-maps with ideals in rings of integers, power-maps and Galois-extension maps.
When all objects and morphisms are labeled it is quite easy to reconstruct the Galois field $L$ from it as well as all maps between prime spectra of rings of integers in intermediate fields, which after all was the intended use of Frobenioids, to ‘dismantle’ these arithmetic schemes and endow them with extra structure given by the power-maps.
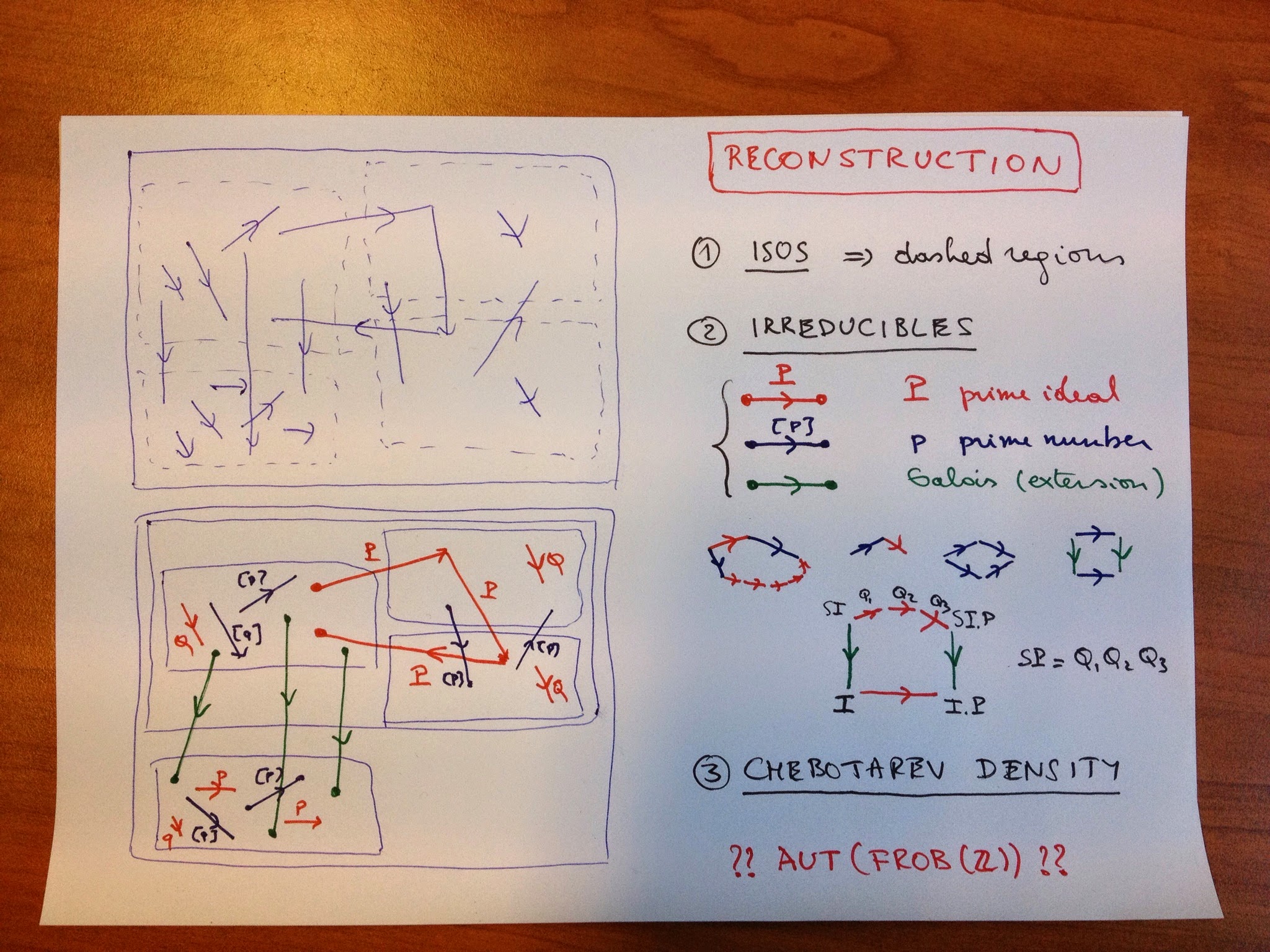
However, in this reconstruction process we are only allowed t use the category structure, so all objects and morphisms are unlabelled (the situation top left) and we want to reconstruct from it the different layers of the Frobenioid (corresponding to the different subfields) and divide all arrows according to their type (situation bottom left).
First we can look at all isomorphisms. They will divide the category in the dashed regions, some of them will be an entire layer (for example for $\mathbb{Q}$) but in general a finite number of these regions will make up the full layer of a subfield (the regions labeled by the elements of the ideal class group).
Another categorical notion we can use are ‘irreducible morphisms’, that is a morphism $f$ which is not an iso but having the property that in each factorisation $f = g \circ h$ either $g$ or $h$ must be an iso. If we remember the different types of morphisms in our Frobenioid we see that the irreducibles come in 3 flavours:
– oRder-maps (Red) : multiplication by a prime ideal $P$ of the ring of integers of the subfield
– froBenius or power-maps (Blue) sendingg a fractional ideal $I$ to $I^p$ for a prime number $p$
– Galois-maps (Green) extending ideals for a subfield $K$ to $K’$ having no intermediate field.
We would like to determine the colour of these irreducibles purely categorical. The idea is that reds have the property that they can be composed with another irreducible (in fact, of power type) such that the composition can again be decomposed in irreducibles and that there is no a priori bound on the number of these terms (this uses the fact that $[p] \circ Q = Q \circ Q \circ … Q \circ [p]$ and that there are infinitely many prime numbers $p$). One checks that compositions of order or Galois maps with irreducibles have factorisation with a bounded number of irreducibles.
The most interesting case is the composition of a Galois map with an order map $P$, this can be decomposed alternatively as order maps in the bigger field followed by a Galois map, the required order maps are the bigger primes $Q_i$ occurring in the decomposition of the extended ideal
\[
S.P = Q_1.Q_2….Q_k \]
but the number $k$ of this decomposition is bounded by the dimension of the bigger field over the smaller one. Summarizing:
– we can determine all the red maps, which will then give us also the different layers
– we can determine the green maps as they move between different layers
– to the remaining blue ones we can even associate their label $[p]$ by the observed property of composition with order maps.
Taking an object in a layer, we get the set of prime ideals of the ring on integers in that field as the set of all red arrows leaving that object unto equivalence (by composing with an isomorphism), so we get the prime spectra $\mathbf{Spec}(S)$.
For a ring-extension $R \rightarrow S$ we also can recover the cover map $\mathbf{Spec}(S) \rightarrow \mathbf{Spec}(R)$
Indeed, composing the composition of the Galois map with the order-map $P$ and decomposing it alternatively will give us the finite number of prime ideals $Q_i$ of $S$ lying over $P$. That is, we get all splitting behaviour of prime ideals in intermediate field-extensions.
Let $K$ be a Galois subfield of $L$ then we have a way to see how a prime ideals in $\mathbf{Spec}(\mathbb{Z})$ splits, ramifies or remains inert in $K$ and so by Chebotarev density this gives us the dimension of $K$ as well as the Galois group. And, if we could label the prime ideal by a prime number $p$, we could even reconstruct $K$ itself as $K$ is determined once we know all prime numbers which completely split.
The problem i have is that i do not see a categorical way to label the red arrows in $Frob(\mathbb{Z})$ by prime numbers. Mochizuki says we can do this in the proof of Thm 6.4(iii) by using the fact that the $log(p)$ are linearly independent over $\mathbb{Q}$.
This suggests that one might use the ‘Arakelov information’ (that is the archimidean valuations) to do this (the bit i left out so far), but i do not see this in the case of $\mathbb{Q}$ as there is just 1 extra (real) valuation determined by the values of the nonarchimidean valuations.
Probably i am missing something so all sorts of enlightenment re welcome!
Leave a Comment