Skip to content →

Category: books

Hexboards and Heytings

Published February 26, 2022 by lievenlb

A couple of days ago, Peter Rowlett posted on The Aperiodical: Introducing hexboard – a LaTeX package for drawing games of Hex.

Hex is a strategic game with two players (Red and Blue) taking turns placing a stone of their color onto any empty space. A player wins when they successfully connect their sides together through a chain of adjacent stones.

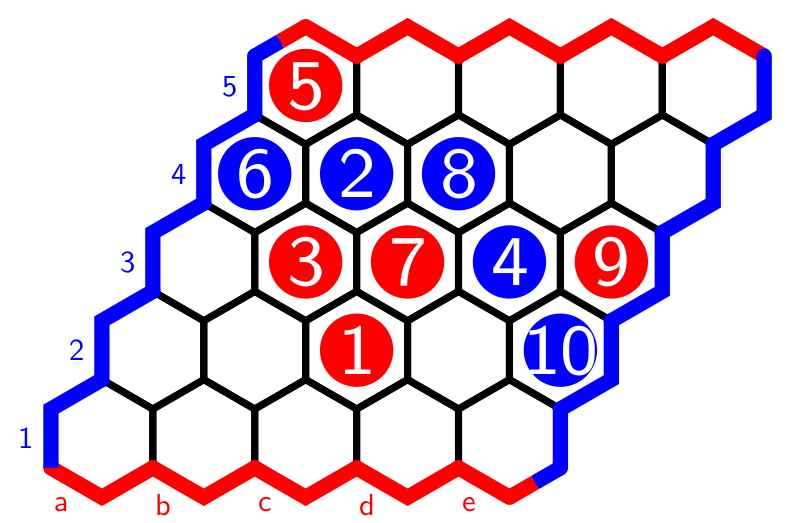
Here’s a short game on a $5 \times 5$ board (normal play uses $11\times 11$ boards), won by Blue, drawn with the LaTeX-package hexboard.



As much as I like mathematical games, I want to use the versability of the hexboard-package for something entirely different: drawing finite Heyting algebras in which it is easy to visualise the logical operations.

Every full hexboard is a poset with minimal cell $0$ and maximal cell $1$ if cell-values increase if we move horizontally to the right or diagonally to the upper-right. With respect to this order, $p \vee q$ is the smallest cell bigger than both $p$ and $q$, and $p \wedge q$ is the largest cell smaller than $p$ and $q$.



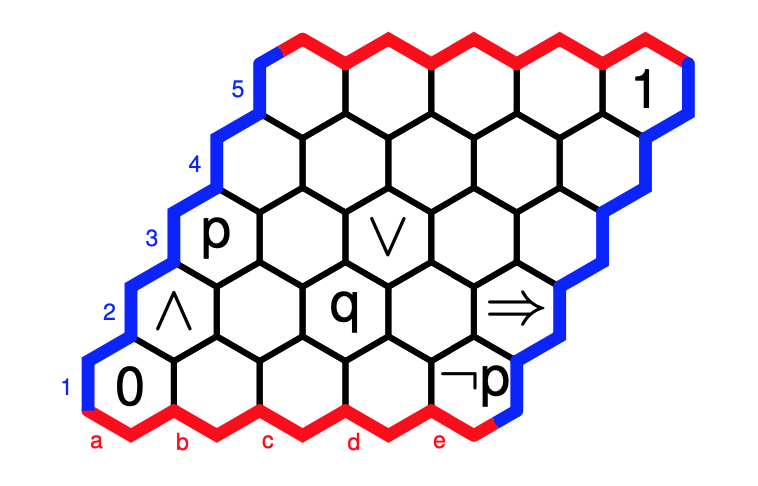
The implication $p \Rightarrow q$ is the largest cell $r$ such that $r \wedge p \leq q$, and the negation $\neg p$ stands for $p \Rightarrow 0$. With these operations, the full hexboard becomes a Heyting algebra.

Now the fun part. Every filled area of the hexboard, bordered above and below by a string of strictly increasing cells from $0$ to $1$ is also a Heyting algebra, with the induced ordering, and with the logical operations defined similarly.



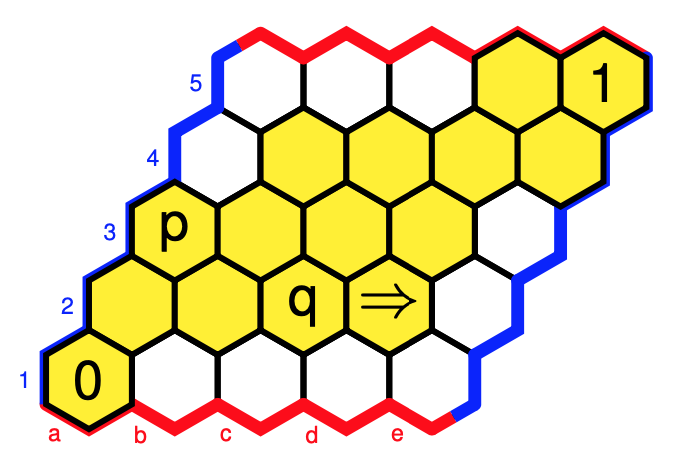
Note that this mustn’t be a sub-Heyting algebra as the operations may differ. Here, we have a different value for $p \Rightarrow q$, and $\neg p$ is now $0$.

If you’re in for an innocent “Where is Wally?”-type puzzle: $W = (\neg \neg p \Rightarrow p)$.



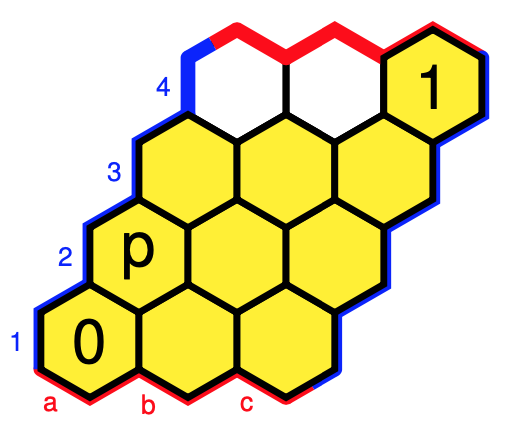
Click on the image to get the solution.

The downsets in these posets can be viewed as the open sets of a finite topology, so these Heyting algebra structures come from the subobject classifier of a topos.

There are more interesting toposes with subobject classifier determined by such hex-Heyting algebras.

For example, the Topos of Triads of Thomas Noll in music theory has as its subobject classifier the hex-Heyting algebra (with cell-values as in the paper):



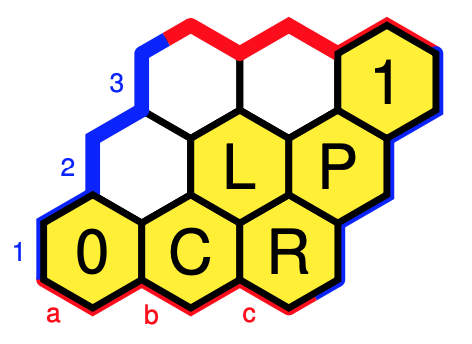
Note to self: why not write a couple of posts on this topos?

Another example: the category of all directed graphs is the presheaf topos of the two object category ($V$ for vertices, and $E$ for edges) with (apart from the identities) just two morphisms $s,t : V \rightarrow E$ (for start- and end-vertex of a directed edge).

The subobject classifier $\Omega$ of this topos is determined by the two Heyting algebras $\Omega(E)$ and $\Omega(V)$ below.



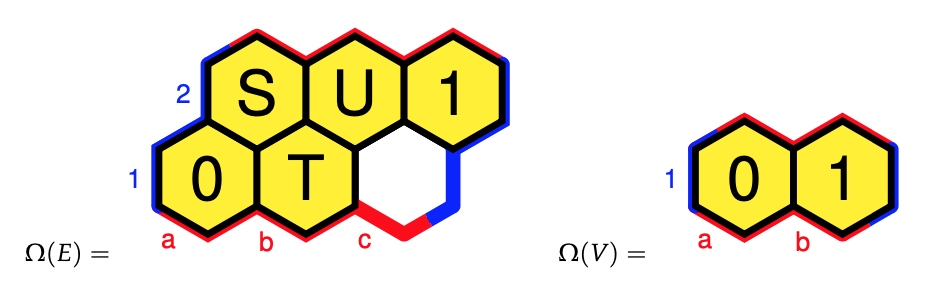
These ‘hex-Heyting algebras’ are exactly what Eduardo Ochs calls ‘planar Heyting algebras’.

Eduardo has a very informative research page, containing slides and handouts of talks in which he tries to explain topos theory to “children” (using these planar Heyting algebras) including:

Perhaps now is a good time to revive my old sga4hipsters-project.

Leave a Comment

Chevalley’s circle of friends

Published February 8, 2022 by lievenlb

Last week, Danielle Couty ArXiVed her paper Friendly views on Claude Chevalley (in French).

From the abstract: “We propose to follow the itinerary of Claude Chevalley during the last twenty years of his life, through the words of Jacques Roubaud, Denis Guedj and Alexander Grothendieck. Our perspective is that of their testimonies filled with friendship.”

Claude Chevalley was one of the founding fathers of Bourbaki. Two of the four pre-WW2 Bourbaki-congresses were held in “La Massoterie”, the Chevalley family domain in Chancay (see this post, update: later I learned from Liliane Beaulieu that the original house was destroyed by fire).

In 1938 he left for Princeton and stayed there during the war, making it impossible to return to a position in France for a very long time. Only in 1957 he could return to Paris where he led a seminar which proved to be essential for the development of algebraic groups and algebraic geometry.



Picture from N. Bourbaki, an interview with C. Chevalley

The Couty paper focusses on the post-1968 period in which Chevalley distanced himself from Bourbaki (some of its members, he thought, had become ‘mandarins’ and ‘reactionaires’), became involved with the ecological movement ‘Survivre et vivre’ and started up the maths department of a new university at Vincennes.

The paper is based on the recollections of three of his friends.

1. Jacques Roubaud is a French poet, writer and mathematician.

On this blog you may have run into Roubaud as the inventor of Bourbaki’s death announcement, and the writer of the book with title $\in$.

He’s also a member of Oulipo, a loose gathering of (mainly) French-speaking writers and mathematicians. Famous writers such as Georges Perec and Italo Calvino were also Oulipo-members (see also Ouilpo’s use of the Tohoku paper).

Chevalley introduced Roubaud (and others) to the game of Go. From Couty’s paper this quote from Roubaud (G-translated):

“. . . it turns out that he had learned to play go in Japan and then, in Paris, he could not find a player […] I played go with him […] and then at a certain moment , we thought, Pierre Lusson and myself, it would still be good to create circumstances such that Chevalley could have players. And so, we had a lot of ambition, we said to ourselves: “We’re going to write a treatise on go, and then lots of people will start playing go”. »

The resulting Go-book is A short treatise inviting the reader to discover the subtle art of Go. Here’s Georges Perec (left) and Jacques Roubaud playing a game.



Picture from Petit traite invitant a la decouverte de l’art subtil du Go

2. Denis Guedj was a French novelist, mathematician and historian of science professor, perhaps best known for his book The Parrot’s Theorem.

In May 1968, Guedj was a PhD-student of Jean-Paul Benzecri (the one defining God as the Alexandroff compactification of the univers), working in the building where ‘Le Comité de Grève’ installed itself. Here he met Chevalley. A Guedj-quote from Couty’s paper (G-translated):

“Claude Chevalley was one of the three professors of the Faculty of Science to commit himself totally to the adventure until the end, occupying the premises with the students on the Quai Saint-Bernard […] and sleeping there frequently . That’s where I met him.

We had taken possession of this universe which until then had only been a place of study and knowledge, and which, in the mildness of this month of May, had become a place of life, of a life wonderfully exhilarating. The college was ours. At night we walked down the aisles yet? lined with tall trees, entered the empty lecture halls, slept under the stars. Needless to say that at the beginning of the school year, in the fall of 1968, it was impossible for us to find our place in these undressed spaces from which the magic had withdrawn. »



Picture from Décès de l’écrivain et universitaire Denis Guedj

In June 2008, Guedj was one of the guests at the special edition of France Culture on the occasion of Grothendieck’s 80th birthday, Autour d’Alexandre Grothendieck.

3. Alexander Grothendieck, mathematician and misogynist, deified by some of today’s ‘mandarins’.

The paper by Danielle Couty may shed additional light on Grothendieck’s withdrawal from Bourbaki and mathematics as a whole. A G-translated Grothendieck quote from the paper:

“It was Chevalley who was one of the first, with Denis Guedj whom I also met through Survivre, to draw my attention to this ideology (they called it “meritocracy” or a name like that), and what there was in her of violence, of contempt. It was because of that, Chevalley told me […] that he could no longer bear the atmosphere in Bourbaki and had stopped setting foot there. »

Claude Chevalley stayed at Vincennes until his retirement in 1978, he died on June 28th 1984.

Leave a Comment

Grothendieck stuff

Published January 30, 2022 by lievenlb

January 13th, Gallimard published Grothendieck’s text Recoltes et Semailles in a fancy box containing two books.



Here’s a G-translation of Gallimard’s blurb:

“Considered the mathematical genius of the second half of the 20th century, Alexandre Grothendieck is the author of Récoltes et semailles, a kind of “monster” of more than a thousand pages, according to his own words. The mythical typescript, which opens with a sharp criticism of the ethics of mathematicians, will take the reader into the intimate territories of a spiritual experience after having initiated him into radical ecology.

In this literary braid, several stories intertwine, “a journey to discover a past; a meditation on existence; a picture of the mores of a milieu and an era (or the picture of the insidious and implacable shift from one era to another…); an investigation (almost police at times, and at others bordering on the swashbuckling novel in the depths of the mathematical megapolis…); a vast mathematical digression (which will sow more than one…); […] a diary ; a psychology of discovery and creation; an indictment (ruthless, as it should be…), even a settling of accounts in “the beautiful mathematical world” (and without giving gifts…)”.”

All literary events, great or small, are cause for the French to fill a radio show.

January 21st, ‘Le grand entretien’ on France Inter invited Cedric Villani and Jean-Pierre Bourguignon to talk about Grothendieck’s influence on mathematics (h/t Isar Stubbe).

The embedded YouTube above starts at 12:06, when Bourguignon describes Grothendieck’s main achievements.

Clearly, he starts off with the notion of schemes which, he says, proved to be decisive in the further development of algebraic geometry. Five years ago, I guess he would have continued mentioning FLT and other striking results, impossible to prove without scheme theory.

Now, he goes on saying that Grothendieck laid the basis of topos theory (“to define it, I would need not one minute and a half but a year and a half”), which is only now showing its first applications.

Grothendieck, Bourguignon goes on, was the first to envision the true potential of this theory, which we should take very seriously according to people like Lafforgue and Connes, and which will have applications in fields far from algebraic geometry.

Topos20 is spreading rapidly among French mathematicians. We’ll have to await further results before Topos20 will become a pandemic.

Another interesting fragment starts at 16:19 and concerns Grothendieck’s gribouillis, the 50.000 pages of scribblings found in Lasserre after his death.

Bourguignon had the opportunity to see them some time ago, and when asked to describe them he tells they are in ‘caisses’ stacked in a ‘libraire’.

Here’s a picture of these crates taken by Leila Schneps in Lasserre around the time of Grothendieck’s funeral.



If you want to know what’s in these notes, and how they ended up at that place in Paris, you might want to read this and that post.

If Bourguignon had to consult these notes at the Librairie Alain Brieux, it seems that there is no progress in the negotiations with Grothendieck’s children to make them public, or at least accessible.

Leave a Comment