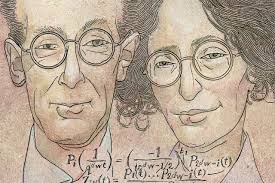Category: books

Le Guide Bourbaki: Aumont-Aubrac

Published June 9, 2025 by lievenlb

Sooner or later, every generation of Bourbakistas is drawn to the natural beauty of the Auvergne-region, known for its mountain ranges and dormant volcanoes.

In the summer of 1935 the founding fathers created Nicolas Bourbaki during their congress in Besse-en-Chandesse.

Standing from left to right: Cartan, de Possel, Dieudonne, Weil and a local technician. Seated from left to right: Mirles (guinea pig), Chevalley and Mandelbrojt.

In August 1954, the remaining founding fathers gathered with second generation Bourbakistas and a bunch of guests at the Hotel des Pins in Murol.

Apart from Cartan, Chevalley, Delsarte, Dieudonne and Weil, present were of the second generation: Dixmier, Godement, Koszul, Eilenberg, Samuel, Schwartz and Serre. There was a guinea-pig (Serge Lang), an ‘efficiency expert’ (Saunders MacLane), two ‘foreign visitors’ (Hochschild and John Tate) and two ‘honorable foreign visitors’ (Iyanaga and Kosaku Yosida).

From left to right, Godement, Dieudonne, Weil, MacLane, and a smug looking Serre (he knew he would be awarded a Fields medal at the coming ICM in a few days time).

For the third generation, the Auvergne-spot of choice was Aumont-Aubrac, now part of Peyre en Aubrac. In Occitan Aumont-Aubrac is called Autmont from the Latin ‘altum montem’, haute montagne (high mountain), appropriate as the average elevation of the commune is 1045m.

‘Tribu 86’ recounts their visit in the fall of 1972, and calls it ‘Le congres des cèpes‘ (the Porcini mushrooms congress).

Bourbaki rediscovered the simple joys: slow-moving trains climbing the Cévennes, mushroom picking, peasant feasts. Douady was mistaken for a horse dealer at the fairground, Cartier was restocking his tools, and Meyer revealed himself to be a mushroom expert.

Bourbaki attracted bad luck; the Ponts-et-Chaussées had chosen his stay to repair the main road, but, despite vigilant monitoring, no notable accidents were observed. The stationmaster, a journalist between two train departures, photographed Bourbaki for the local gazette, and delayed the departure of the train for Paris to allow Yvonne Verdier and Demazure to finish their pie.

From ‘Tribu 85’ we learn that they stayed in ‘Hotel de la Gare’, and arrived by night-train from Paris.

The ‘Grand Hotel de la Gare’ aka ‘Grand Hotel Prouheze’ was run by the Prouheze family but is now closed.

‘Tribu 85’, which is the account of their previous summer congress in Cabris (called ‘The water congress’) contains:

The sky took it upon itself to suggest the title of the conference; one rarely sees so much rain at La Messuguière, perhaps to mourn its impending closure.

Perhaps it was due to the bad weather at Cabris last time, or the fear of unavailability of their favourite ‘Villa La Messuguière’, or their enjoyable stay at Aumont-Aubrac in the fall of 1972, anyway Bourbaki decided to have their summer 1973 congress again in Aumont-Aubrac, and again at the Hotel de la Gare (as we can learn from La Tribu 87).

A large group gathered on the evening of June 5th 1973, this time with their bicycles, to take the night train from Paris to Aumont-Aubrac: Hyman Bass, Louis Boutet de Monvel, François Bruhat, Pierre Cartier, Michel Demazure, Adrien Douady (with his wife Regine), André Gramain, Barry Mazur (with his wife Gretchen and their son Zeke), Michel Raynaud, Jean-Louis Verdier, and Jean-Marc Fontaine (with his wife Laurence).

Determined to get to know the real country in the absence of the p-adic country, Bourbaki returned a second time to his Auvergnian roots (Besse 1935!).

Thanks to the organisational progress of the SNCF, which now runs sleeper bike trains, and to the Fontaines who brought their car, Bourbaki did not lack means of transportation. They were necessary to ensure the connection between Bourbaki’s two bases.

Le Moulin, four kilometers from Aumont, increasingly better equipped, allowed for serious discussions to alternate with the sounds of bourrée and the sipping of lemonade and beer. A large fire chased away evil spirits and the threat of colds.

Bourbaki, ever the genius, chose as his base the pigs’ den, where he had ten thousand hectares of flowering and fragrant meadows.

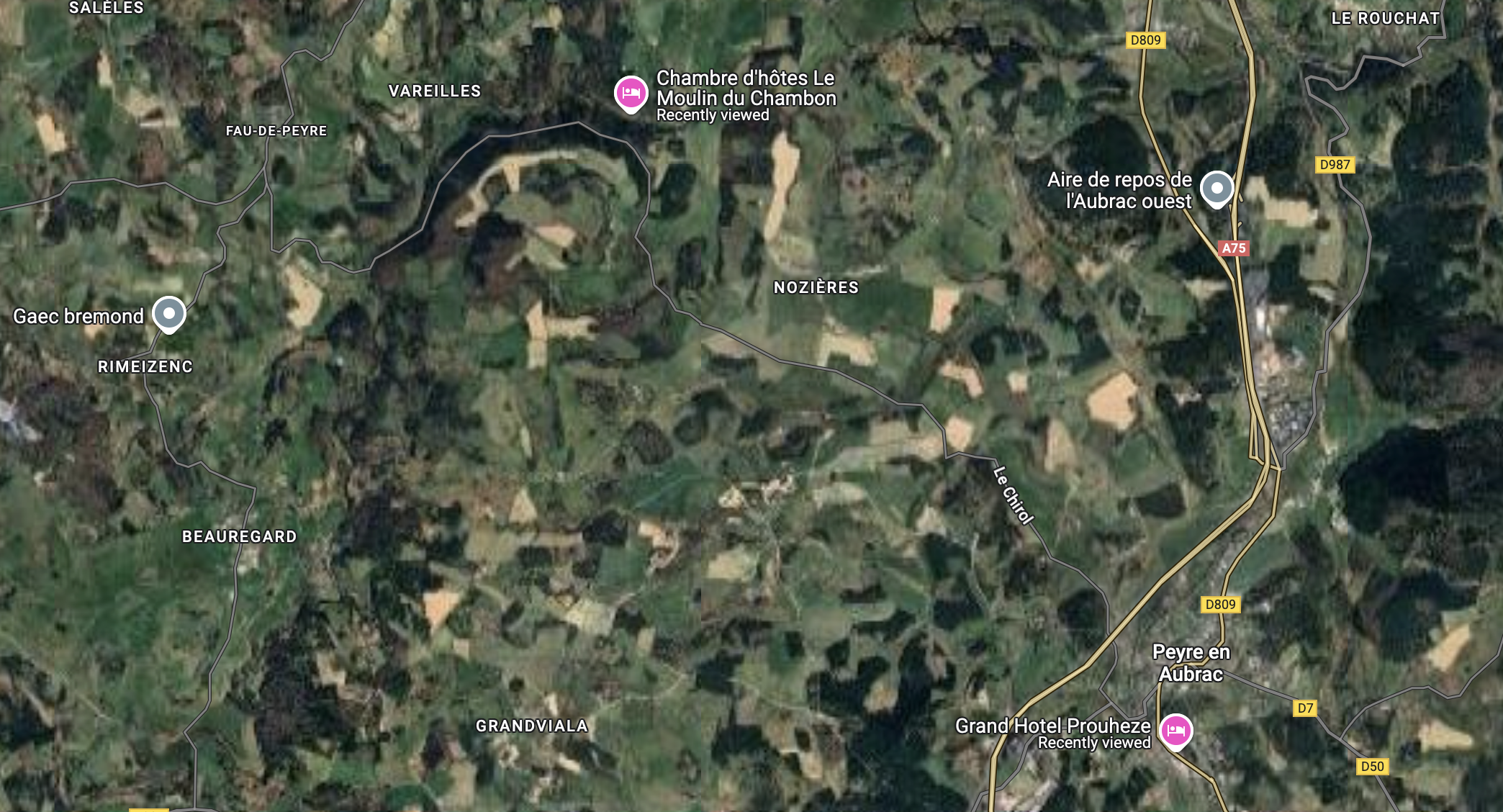
‘Le Moulin’, Bourbaki’s ‘second base’ in the country is now the Chambres d’Hotes au Moulin du Chambon and lies indeed 4km from Aumont-Aubrac, and has indeed a large fireplace, a nice cantou.

Back then, it probably was a pub and the endpoint of several afternoon bicycle excursions for the Bourbakis.

The high point of the congress was their bicycle ‘tour du Gevaudan’. The Gevaudan is the old name of what is now the Lozère département. The name was derived from the Gabali, a Gallic tribe.

Today, the name Gevaudan lives on in the story of the beast of Gevaudan, which killed between 82 and 124 people between June 30, 1764 to June 19, 1767. There’s a statue of the beast in front of the Hotel-de-Ville in Aumont-Abrac.

Previously in this series

Comments closed

Vialism versus Weilism

Published June 2, 2024 by lievenlb

Here’s how 21 pilots themselves define Vialism, the ‘religion’ of Dema, in the ‘I am Clancy’ video:

Their authority comes from two things: a miraculous power and a hijacked religion. One feeds the other. A cycle. It’s called Vialism, and all you really need to know is that it teaches that self-destruction is the only way to paradise.

Some people think that Vialism means Weilism, after the Weil siblings Andre and Simone.

Simone Weil (1909-1943) was a French philosopher and political activist. In her later years she became increasingly religious and inclined towards mysticism.

Andre Weil (1906-1998) was a French mathematician and founding member of the Bourbaki group.

They enter the lore via a picture on Tyler Joseph’s desktop in the Zane Lowe interview in 2018, which is an overlay of two photographs of Bourbaki meetings in 1937 and 1938 featuring Andre and Simone.

For Simone this is the crucial period in her conversion to Catholicism, for Andre these meetings led to a reformulation of the foundations of TOPology, and discussions on Bourbaki’s version of Set theory which would lead to Bourbaki’s first book, published in 1939.

Both topics left a lasting impression on Simone Weil, as she wrote in 1942:

One field of mathematics that deals with all the diverse sorts of orders (set theory and general topology) is a treasure-house that holds an infinity of valuable expressions that show supernatural truth.

Now, Simone was fairly generous in her use of the adjective ‘supernatural’. Here’s another quote:

“The supernatural greatness of Christianity lies in the fact that it does not seek a supernatural remedy for suffering but a supernatural use for it.”

This suggests that if Vialism really is Weilism, then the ‘miraculous power’ might be mathematics (or at least the topics of set theory and topology), and the ‘hijacked religion’ might be the (ab)use of mathematics in theology.

Roughly speaking, axiomatic Zermelo-Fraenkel set theory gives a precise list of instructions to construct all sets out of two given sets, the empty set $\emptyset$ (the set containing nothing) being one of them.

Emptiness, or the void, is important in Simone Weil’s theology, see for example her book Love in the void: where God finds us

or consider this quote by her:

God stripped himself of his godhood and became empty, and fulfilled us with false godhood. Let us strip off this false godhood and become empty. This very act is the ultimate purpose to creating us.

which sounds a lot like Vialism, becoming an ’empty vessel’ for the Bishops (or God) to fill.

Also in 21 pilots’ iconography, the empty set $\emptyset$ is important.

Btw. the symbol $\emptyset$ for the empty set was first used by Andre Weil who remembered the Norwegian ‘eu’ from his studies of nordic languages preparing for his ‘Finnish fugue’ in 1939.

The other pre-given set challenges the Gods and theology. The Axiom of Infinity in the Zermelo-Fraenkel system asserts the existence of an infinite set, usually denoted $\omega$ and interpreted as the set of all finite numbers $\{ 0,1,2,3,4,5,6,\dots \}$.

In other words, mathematical set theory contains an object which is actual infinity!

From the ancient Greeks on to early modern times, philosophers adhered to the motto “Infinitum actu non datur”, there is only a potential infinity (the idea of infinity) but actual infinity belongs to the realm of the Gods (infinite power, infinite wisdom,…).

As if this was not heretic enough, in comes Georg Cantor.

Georg Cantor (1845-1918) might very well be another Clancy.

He was a German mathematician, discoverer of the secrets of infinity, which brought him in conflict with several influential mathematicians in his time (notably Kronecker and Poincare), and inventor of Cardinal numbers (compare Bishops).

He suffered from depression and mental illness, was often admitted to the Halle nerve clinic. In between he was a founding member of the DEutscher MAthematiker Vereinigung (DeMa) of which he was the first president (Nico), he suffered from malnourishment during WW1 (compare Simone Weil in WW2) and died of a heart attack in the sanatorium where he had spent the last year of his life.

Cantor showed that the only distinguishing feature between two sets is their Cardinality (Bishopy power), roughly speaking the number of things they contain. He then showed that for every set of a certain Bishopy power, there’s one of even higher power!

For example, there exists a set with higher cardinality than $\omega$, that is, a set we cannot enumerate. An example is described in these lines from Morph

Lights they blink to me, transmitting things to me
Ones and zeroes, ergo this symphony
Anybody listening? Ones and zeroes
Count to infinity, ones and zeroes

They’re talking about all possible infinite series of $0$’s and $1$’s and one quickly proves that these cannot be enumerated using Cantor’s diagonal argument.

When applied to theology this says that Gods cannot have any actual infinity power, for there’s always an entity posessing higher powers.

That’s why Cantor resolved to God being ‘absolute infinity’, the Bishopy power of the class of all cardinal numbers (emphasis only important for mathematicians).

Much more on the interplay between Cantor’s mathematical results on infinities and his theological writings can be found in the paper Absolute Infinity: A Bridge Between Mathematics and Theology? by Christian Tapp.

The compassionate God of Christianity has presented theologians for centuries with the following paradox: how can a God having infinite power suffer because humans suffer?

In comes TOPology and one of its founding fathers Felix Hausdorff.

Felix Hausdorff (1868-1942) might very well be another Clancy.

He was a German mathematician who made substantial contributions to topology as well as set theory. For years he felt opposition because he was Jewish.

After the Kristallnacht in 1938 he tried to escape Nazi-Germany (DeMa) but couldn’t obtain a position in the US. On 26 January 1942, Felix Hausdorff, along with his wife and his sister-in-law, died by suicide, rather than comply with German orders to move to the Endenich camp.

He was also a philosopher and writer under the pseudonym Paul Mongré. In 1900 he wrote a book of poems, Ecstasy, of which the first poem is “Den Ungeflügelten” (To The Wingless Ones). Am I the only one to think immediately of The isle of the flightless birds?

Anyway, as to how the topology of Weilism solves the contradiction of the suffering God of Christianity is explained in the paper The Theology of Simone Weil and the Topology of Andre Weil by Ochiai Hitoshi, professor of ‘Mathematical Theology’ at Doshisha University, Kyoto.

He has a follow-up post Incarnation and Reincarnation on the Apeiron Centre (where he also has a post on the Theology of Georg Cantor). Here’s a summary of his thesis:

God is Open
Incarnation is Compactified God
The soul is Open
Reincarnation is Compactified Soul
God and the Soul are Homeomorphic
God is without Boundaries
The soul is with Boundaries
God and the Soul are not Diffeomorphic

This succinctly sums up Weilism for you.

I now understand why so many people in the 21 pilots sub-Reddit thought at the beginning of the Trench-era that Bourbaki was a group of mathematicians trying to prove the existence of God.

In the paper The Theology of Simone Weil and the Topology of Andre Weil the next quote is falsely attributed to Bourbaki

God is the Alexandroff compactification of the universe.

If you are interested in the history behind this quote you may read my post According to Groth. IV.22.

If you want an alternative explanation of Vialism, you may read my post Where’s Bourbaki’s Dema?.

Btw. I forgot to mention in that post the “Annual Assemblage of the Glorified”. Since 1918 this takes place November 11th, on Armistice Day.

In this series:

What about Simone Weil?

Published May 13, 2024 by lievenlb

In recent weeks, a theory that Simone Weil is the key to Dema-lore is getting a lot of traction.

Image credit

In two words, this theory is based on the assumption that Vialism=Weilism and on textual similarities between the writings of Simone Weil and the lyrics of 21 pilots and the Clancy letters.

The Keons YouTube channel explains this in great detail.

Until now, I thought that Andre Weil was crucial to the story, and that Simone’s role was merely to have a boy/girl archetypical situation.

There’s this iconic photograph of them from 1922, taken weeks before Andre entered the ENS:

The same setting, boy on the left, girl to the right was used in the Nico and the niners-video, when they are young and in Dema

and when they are a quite a bit older, and in Trench, at the end of the Outside-video.

These scenes may support my theory that Dema was the ENS (both Andre and Simone studied there) as is explained in the post Where’s Bourbaki’s Dema?, and when they were both a bit older, and at the Bourbaki meetings in Chancay and Dieulefit, that they were banditos operating in Trench, as explained in the post Bourbaki = Bishops or Banditos.

There are two excellent books to read if you want to know more about the complex relationship between Andre and Simone Weil.

The first one is The Weil Conjectures: On Math and the Pursuit of the Unknown by Karen Olsson.

From it we get the impression that, at times, Simone felt intellectually inferior to Andre, who was three years older. She often asked him to explain what he was working on. Famous is his letter to her written in 1940 when he was jailed. Here’s a nice Quanta-article on it, A Rosetta stone for mathematics. This was also the reason why she wanted to attend some Bourbaki-meetings in order to get a better understanding of what mathematics was all about and how mathematicians think.

She was then very critical about mathematics because all that thinking about illusory objects had no immediate effect in real life. Well Simone, that’s the difference between mathematics and philosophy.

The second one is Chez les Weil, Andre et Simone written by Andre’s eldest daughter Sylvie.

From it we get another impression, namely that Andre may have been burdened by the fact that, after Simone’s death, his parents life centered exclusively around the preservation of her legacy, ignorant of the fact that their remaining child was one of the best mathematicians of his generation.

Poor Andre, on their family apartment in the Rue Auguste-Comte (which Andre used until late in his life when he was in Paris) is now this commemorative plaque

Well Andre, that’s the difference between a mathematician and a philosopher.

Let’s return to the role Simone Weil may play in Dema-lore. For starters, how did she appear in it?

She makes her appearance through a picture on Tyler’s desktop at the start of the Trench-era. This picture is a combination of two photographs from Bourbaki meetings, and Simone Weil features in both of them.

The photograph on the left is from the september 1937 meeting in Chancay, that on the right is from the september 1938 meeting in Dieulefit.

These are exactly the years crucial in Simone’s conversion to catholicism.

In the spring of 1937 she experienced a religious ecstasy in the Basilica of Santa Maria degli Angeli in Assisi.

Over Easter is 1938, Simone and her mother attended Holy Week services at the Solesmes Abbey where she had a mystic experience in which “Christ himself came down and took possession of me”.

One might ask whether there’s any connection between these religious experiences and her desire to attend these upcoming Bourbaki meetings. So, what was discussed during these conferences?

Mathematically, the 1938 meeting was not very exciting. Hardly any work was done, as they were preoccupied with all news of the Nazis invading Czechoslovakia. During the conference, Simone and Alain even escaped to Switzerland because they were convinced war was imminent. After a couple of days the Munich Treaty was signed, and Alain returned to Dieulefit, whereas Simone stayed in Switzerland, before returning to Paris.

On the other hand, the Chancay meeting was revolutionary as the foundations of topology were rewritten there with the introduction of the filter concept, dreamed up on the spot by Henri Cartan (the guy in the deckchair), while the others were taking a walk.

Simone was pretty impressed by the power of TOPology. In 1942 she wrote in her ‘Cahiers’:

One field of mathematics that deals with all the diverse sorts of orders (set theory and general topology) is a treasure-house that holds an infinity of valuable expressions that show supernatural truth.

Interestingly, she mentions the two math-subjects closest to the pilots’ universe: set theory studies all objects you can make starting from the empty set $\emptyset$, and topology studies the properties of objects and figures that remain unchanged even when you
morph them.

We’ll have to say more about this in a next post when we look into the Vialism=Weilism assumption.

Another appearance of Simone Weil in the lore might be through the cropped image you can find on the dmaorg-website.

The consensus opinion is that this is a picture of the young Clancy, next to one of the Bishops (Keons? Andre? Nico?).

In fact, the ‘little boy’ is actually a girl and her identity is unresolved as far as I know. But, given the date of the photograph (1956) the girl might be (mistakingly) taken for Andre’s daughter Sylvie.

Now, almost everyone, in particular her grandparents and Andre himself, found that Sylvie was a spitting image (almost a ‘copy’) of Simone Weil.

There are further indications that Simone Weil might be a Clancy.

Morph

In Morph there are these lines

He’ll always try to stop me, that Nicolas Bourbaki
He’s got no friends close, but those who know him most know
He goes by Nico
He told me I’m a copy
When I’d hear him mock me, that’s almost stopped me

During the meetings she attended, the other Bourbakis mocked Simone that she was a copy of het brother. From Karen Olsson’s book mentioned above:

To the others it’s startling to see his same glasses, his same face attached to this body clothed in an. unstylish dress and an off-kilter brown beret, carrying on in that odd monotone as she argues, via the chateau’s telephone, with the editors who publish her political articles.

Early in her career, Simone Weil was far from an original thinker. For her end-essay on Descartes she got the lowest score possible in order to pass from the ENS. Even Andre urged her to have a work-plan to develop her own ideas, rather than copying ideas from philosophers from the past.

Jumpsuit

Whereas Andre tried everything to avoid the draft, Simone was more of a warrior. In 1935 she volunteered to fight on the Republican side in the Spanish civil war, until a kitchen accident forced her to return to France.

Later in 1943 she left New-York to return to England and enlist in the French troupes of General de Gaulle, hoping to be parachuted behind enemy lines. Given her physical state, the military command decided against it. Upset by this refusal, she felt she had no other option than to deny herself food in empathy with the starving French.

She didn’t succeed in crossing Paladin Strait, sorry the Channel.

Overcompensate

Can this be Simone Weil?

In this series:

2 Comments