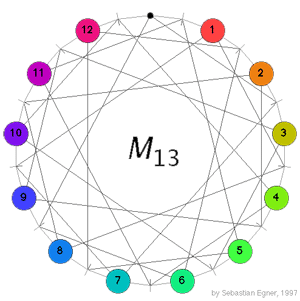
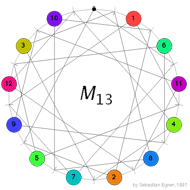
 Conway’s puzzle M(13) is a variation on the 15-puzzle played with the 13 points in the projective plane $\mathbb{P}^2(\mathbb{F}_3) $. The desired position is given on the left where all the counters are placed at at the points having that label (the point corresponding to the hole in the drawing has label 0). A typical move consists in choosing a line in the plane going through the point where the hole is, choose one of the three remaining points on this line and interchange the counter on it for the hole while at the same time interchanging the counters on the other two points. In the drawing on the left, lines correspond to the little-strokes on the circle and edges describe which points lie on which lines. For example, if we want to move counter 5 to the hole we notice that both of them lie on the line represented by the stroke just to the right of the hole and this line contains also the two points with counters 1 and 11, so we have to replace these two counters too in making a move. Today we will describe the groupoid corresponding to this slide-puzzle so if you want to read on, it is best to play a bit with Sebastian Egner’s M(13) Java Applet to see the puzzle in action (and to use it to verify the claims made below). Clicking on a counter performs the move taking the counter to the hole.
Conway’s puzzle M(13) is a variation on the 15-puzzle played with the 13 points in the projective plane $\mathbb{P}^2(\mathbb{F}_3) $. The desired position is given on the left where all the counters are placed at at the points having that label (the point corresponding to the hole in the drawing has label 0). A typical move consists in choosing a line in the plane going through the point where the hole is, choose one of the three remaining points on this line and interchange the counter on it for the hole while at the same time interchanging the counters on the other two points. In the drawing on the left, lines correspond to the little-strokes on the circle and edges describe which points lie on which lines. For example, if we want to move counter 5 to the hole we notice that both of them lie on the line represented by the stroke just to the right of the hole and this line contains also the two points with counters 1 and 11, so we have to replace these two counters too in making a move. Today we will describe the groupoid corresponding to this slide-puzzle so if you want to read on, it is best to play a bit with Sebastian Egner’s M(13) Java Applet to see the puzzle in action (and to use it to verify the claims made below). Clicking on a counter performs the move taking the counter to the hole.
For the 15-puzzle I’ve gone to great lengths of detail here and there explaining how a groupoid naturally crops up having as its objects the reachable positions and as its morphisms the legal slide-sequences. Here, I’ll economize on details. We can encode a position by a permutation in $S_{13} $ by recording the counters (the hole having counter 0) as we move along the circle clockwise starting at the point of label 0 (the top-point). Basic moves transpose two pairs of counters so are given by a product of two transpositions. For example, the move described above from the initial position is $~(0,5)(1,11) $. Again it is clear how to make a groupoid from the reachable positions and the legal move-sequences and how all actual calculations can be done inside the group $S_{13} $. Two small remarks. (1) The situation is more symmetric than in the 15-puzzle. Here we have precisely 12 possible basic moves from any given position corresponding to the 12 non-hole counters which can be thrown into the hole. (2) Related to this, we have another way to encode move-sequences here. For each basic move we can jot down the label of the point whose counter we will throw to the hole (note : label, not counter!). The point of this being that we can now describe all reachable positions having the hole at the top point (the label 0 point) as those obtained from a move sequence of the form $~[0-i_1-i_2-\ldots-i_k-0]~ $ for all choices of $i_j $ between 0 and 12. However, not all these sequences give different positions and we want to determine how many distinct such positions we have. They will again form a subgroup of $S_{12} $ and the aim will be to show that this subgroup is the sporadic simple Mathieu group $M_{12} $. We will check now that $M_{12} $ is contained in this group. _Next time_ we will prove the other inclusion.
Clearly, there are several different ways to label the 13 points and lines in the projective plane and unfortunately the choice of the Conway-Elkies-Martin paper is different from that of the Java Applet. For example, in the Applet-labeling {1,3,4,8} are on a line, whereas the paper-labeling assumes the following point/line labels
$l_0 = \{ 0,1,2,3 \}, l_1= \{ 0,4,5,6 \}, l_2 = \{ 0,9,10,11 \}, l_3 = \{ 0,7,8,12 \}, l_4= \{ 1,4,8,9 \} $
$l_5 = \{ 1,6,7,11 \}, l_6= \{ 1,5,10,12 \}, l_7= \{ 3,5,8,11 \}, l_8 = \{ 3,4,7,10 \} $
$l_9=\{ 2,4,11,12 \}, l_{10}=\{ 2,6,8,10 \}, l_{11}=\{ 2,5,7,9 \}, l_{12} = \{ 3,6,9,12 \} $
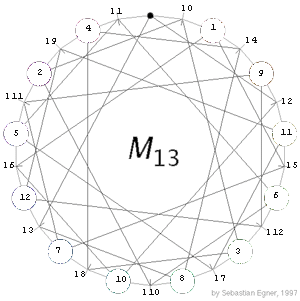 We need to find a dictionary between the two labeling-systems. Again there are several options, but here is the first one I found. Relabeling the points of the Applet as on the left (also indicated is the labeling of the lines)
We need to find a dictionary between the two labeling-systems. Again there are several options, but here is the first one I found. Relabeling the points of the Applet as on the left (also indicated is the labeling of the lines)
we get the labeling of the paper. Hence, to all CEM-paper-sequences we have to apply the dictionary
0(0), 1(1), 2(11), 3(5), 4(12), 5(10), 6(4), 7(8), 8(6), 9(2), 10(7), 11(3), 12(9)
and use the bracketed labels to perform the sequence in the Java Applet. For example, if Conway-Elkies-Martin compute the effect of the move-sequence [0-11-7-9-8-3-0] (read from left to right) then we first have to translate this via the dictionary to the move-sequence [0-3-8-2-6-5-0]. Then, we perform this sequence in the Java-applet (note again : a basic move is indicated by the label of the point to click on NOT the counter) and record the final position.
Below we depict the final positions for the three move-sequences [0-3-8-2-6-5-0], [0-9-1-2-0-5-6-12-0] and [0-1-8-0-5-4-0-1-8-0] which are our translations of the three basic move-sequences on page 9 of the CEM-paper (from left to right).
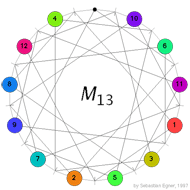
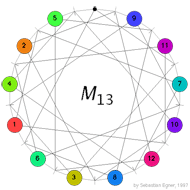
This gives us three reachable positions having their hole at the top. They correspond to teh following permutations in the symmetric group $S_{12} $ (from left to right)
$\alpha = (1,10,8,7,2,6,5,3,11,12,4), \beta=(1,9)(2,11)(3,7)(4,10)(5,12)(6,8) $
$ \gamma=(2,6)(3,11)(5,8)(10,12) $
Using GAP (or the arithmetic progression loop description of $M_{12} $ as given in Chp.11 section 18 of Conway-Sloane modulo relabeling ) we find that the group generated by these three elements is simple and of order 95040 and is isomorphic to the sporadic Mathieu group $M_{12} $.
This corresponds to the messy part of the 15-puzzle in which we had to find enough reachable positions to generate $A_{15} $. The more conceptual part (the OXO-labeling showing that all positions must belong to $A_{15} $) also has a counterpart here. But, before we can tell that story we have to get into linear codes and in particular the properties of the _tetra-code_…
Reference
John H. Conway, Noam D. Elkies and Jeremy L. Martin “The Mathieu Group $M_{12} $ and its pseudogroup extension $M_{13} $” arXiv-preprint
2 Comments