SNORT, invented by Simon NORTon is a map-coloring game, similar to COL. Only, this time, neighbours may not be coloured differently.
SNORTgo, similar to COLgo, is SNORT played with go-stones on a go-board. That is, adjacent stones must have the same colour.
SNORT is a ‘hot’ game, meaning that each player is eager to move as most moves will improve your position. In COL players are reluctant to move, because a move limits your next moves.
For this reason, SNORT positions are much harder to evaluate, and one needs the full force of Conways’s ONAG.
Here’s a SNORTgo endgame. Who has a winning strategy?, and what is the first move in that strategy?
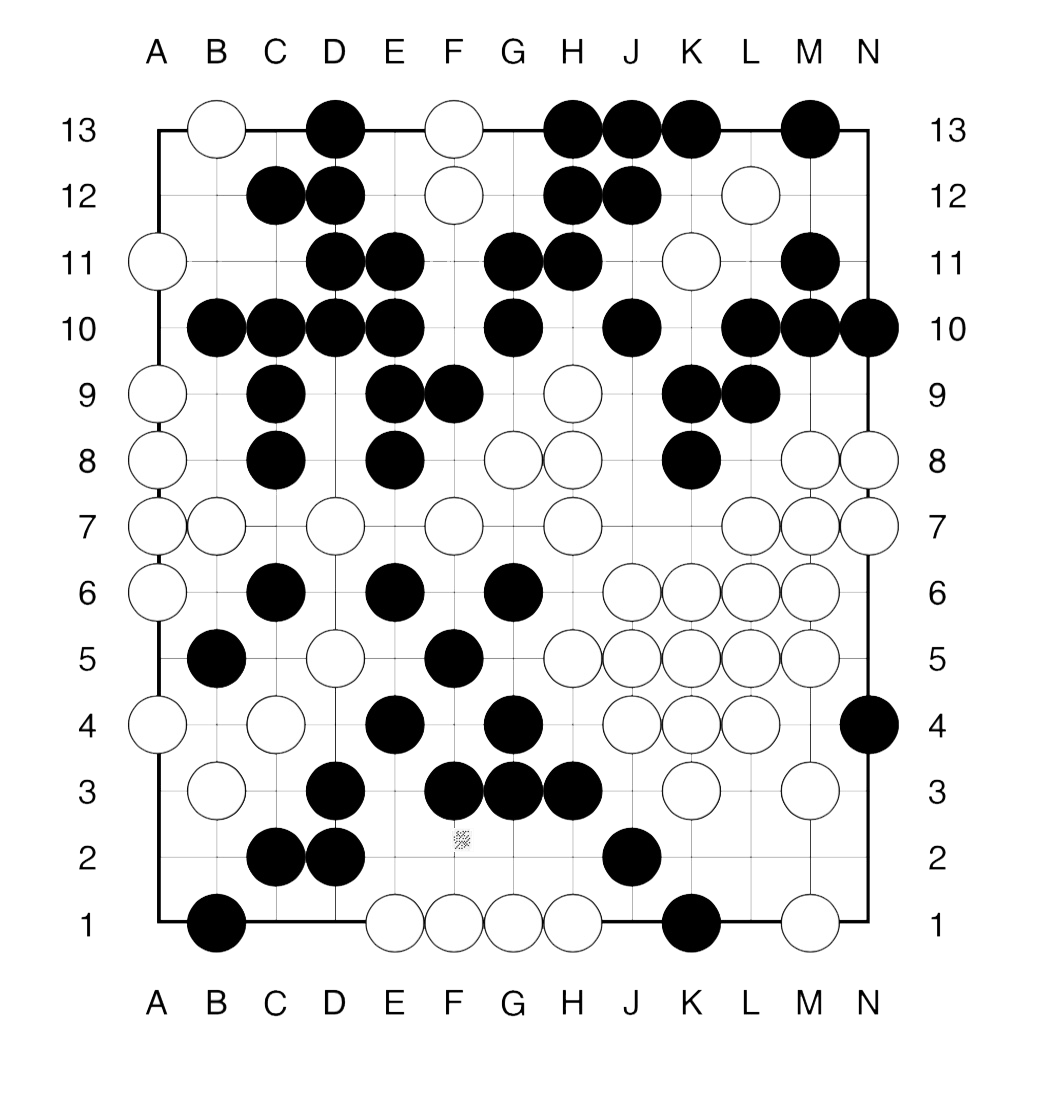
The method to approach such an endgame is similar to that in COLgo. First we remove all dead spots from the board.
What remains, are a 4 spots available only to Right (white) and 5 spots available only to Left (bLack). Further, there a 3 ‘live’ regions: the upper righthand corner and the two lower corners.
The value of these corners must be computed inductively.
Here’s the answer:
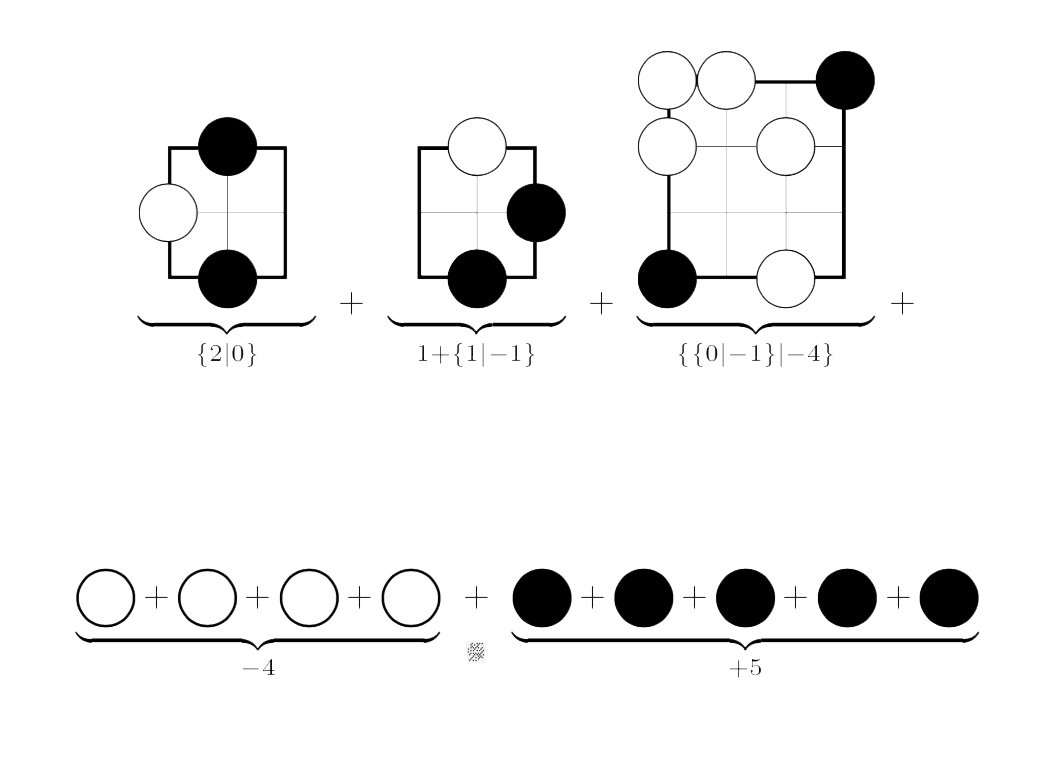
For example, Right’s best option in the left-most game (corresponding to the upper righthand corner of the endgame) is to put his stone on N12, resulting in a game in which neither player can move (the zero game).
On the other hand, Left can put a stone at either N11, N12 or N13 leaving a game in which she has two more moves, whereas Right han none (the $2$ game).
The other positions are computed similarly.
To get the value of the endgame we have to sum up all these values.
This can either be done using the addition rule given in ONAG, or by using programs in combinatorial game theory.
There’s Combinatorial Game Suite, developed by Aaron Siegel. But, for some reason I can no longer use it on macOS High Sierra.
Fortunately, the older program David Wolfe’s toolkit is still available, and runs on my MacBook.
The sum game evaluates to $\{ \{3|2 \}|-1 \}$, which is a ‘fuzzy’ game, that is, its value is confused with $0$.
This means that the first player to move has a winning strategy in the endgame.
Can you spot the (unique) winning move for Right (white) and one (of two) winning move for Left (bLack)?
Spoiler alert : solution in the comments.
One Comment