Monstrous moonshine associates to every element of order $n$ of the monster group $\mathbb{M}$ an arithmetic group of the form
\[
(n|h)+e,f,\dots \]
where $h$ is a divisor of $24$ and of $n$ and where $e,f,\dots$ are divisors of $\frac{n}{h}$ coprime with its quotient.
In snakes, spines, and all that we’ve constructed the arithmetic group
\[
\Gamma_0(n|h)+e,f,\dots \]
which normalizes $\Gamma_0(N)$ for $N=h.n$. If $h=1$ then this group is the moonshine group $(n|h)+e,f,\dots$, but for $h > 1$ the moonshine group is a specific subgroup of index $h$ in $\Gamma_0(n|h)+e,f,\dots$.
I’m sure one can describe this subgroup explicitly in each case by analysing the action of the finite group $(\Gamma_0(n|h)+e,f,\dots)/\Gamma_0(N)$ on the $(N|1)$-snake. Some examples were worked out by John Duncan in his paper Arithmetic groups and the affine E8 Dynkin diagram.
But at the moment I don’t understand the general construction given by Conway, McKay and Sebbar in On the discrete groups of moonshine. I’m stuck at the last sentence of (2) in section 3. Nothing a copy of Charles Ferenbaugh Ph. D. thesis cannot fix.
The correspondence between the conjugacy classes of the Monster and these arithmetic groups takes up 3 pages in Conway & Norton’s Monstrous Moonshine. Here’s the beginning of it.
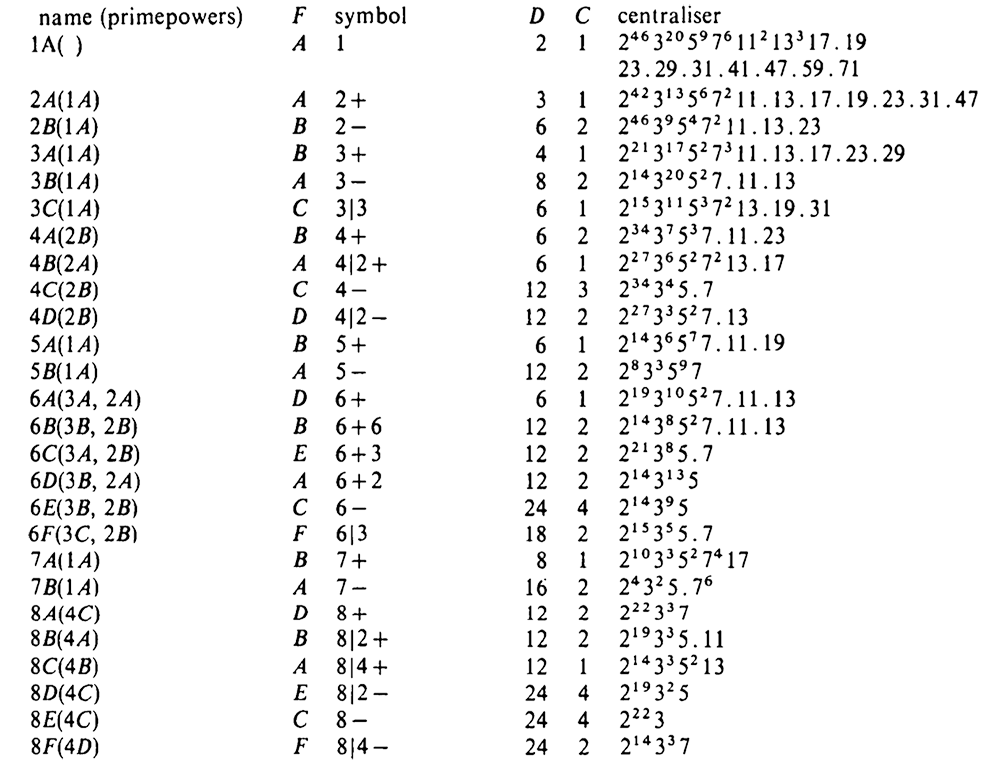
Comments