Chomp is a 2-player game, usually played with chocolate bars.
The players take turns in choosing one chocolate block and “eat it”, together with all other blocks that are below it and to its right. There is a catch: the top left block contains poison, so the first player forced to eat it dies, that is, looses the game.
If you start with a rectangular bar, the first player has a winning strategy, though it may take you too long to actually find the correct first move. See this post for the strategy-stealing argument.
If you label the blocks of the rectangular bar by $(a,b)$ with $0 \leq a \leq k$ and $0 \leq b \leq l$, with the poisonous one being $(0,0)$, then this can be viewed as choosing a divisor $d$ of $N=p^k q^l$ and removing all multiples of $d$ from the set of divisors of $N$. The first person forced to name $1$ looses.
This allows for higher dimensional versions of Chomp.
If you start with the set of all divisors of a given natural number $N$, then the strategy-stealing argument shows that the first player has a winning move.
A general position of the game corresponds to a finite set of integers, closed under taking divisors. At each move the player has to choose an element of this set and remove it as well as all its multiples.
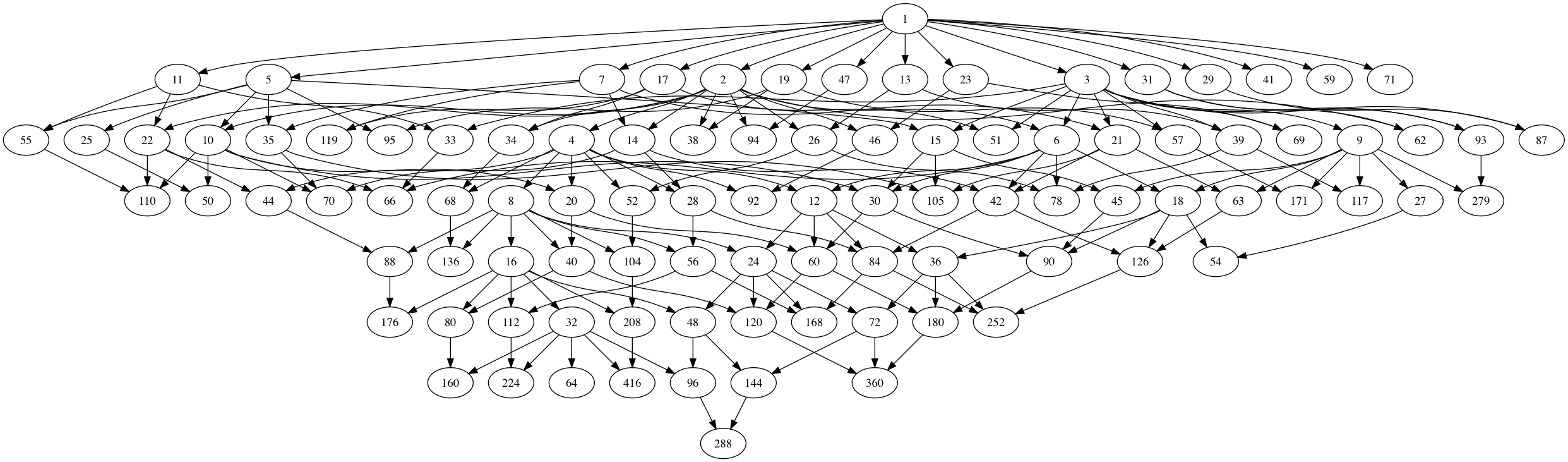
The thread of $(N|1)$, relevant in understanding a moonshine group of the form $(n|m)+e,f,\dots$ with $N=n \times h$, consists of all divisors of $N$.
But then, the union of all threads for all 171 moonshine groups is a position in higher dimensional Chomp.
Who wins starting from this moonshine thread?
Perhaps not terribly important, but it forces one to imagine the subgraph of the monstrous moonshine picture on the $97$ number-lattices way better than by its Hasse diagram.
Click on the image for a larger version.
By the way, notice the (slight) resemblance with the ‘monstrous moonshine painting’ by Atria

Here’s how the Hasse diagram of the moonshine thread was produced. These are ‘notes to self’, because I tend to forget such things quickly.
1. Work though the list of 171 moonshine groups in Monstrous Moonshine, pages 327-329. Add to a list all divisors of $N$ for a group of type $N+e,f,\dots$ or $n|h+e,f,\dots$ with $N=n \times h$. This should give you these $97$ integers:
1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,
31,32,33,34,35,36,38,39,40,41,42,44,45,46,47,48,50,51,52,54,55,56,57,59,60,62,
63,64,66,68,69,70,71,72,78,80,84,87,88,90,92,93,94,95,96,104,105,110,112,117,
119,120,126,136,144,160,168,171,176,180,208,224,252,279,288,360,416
2. Let $L$ be this list and use Sage:
P=Poset((L,attrcall("divides")),linear_extension=True)
H=P.hasse_diagram()
H.graphviz_string()
3. Copy the output to a file, say chomp.dot, and remove all new-line breaks from it.
4. Install Graphviz on Mac OS X.
5. In Terminal, type
dot -Tpng chomp.dot -o chomp.png
Comments