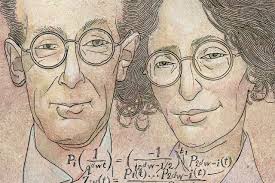Here’s how 21 pilots themselves define Vialism, the ‘religion’ of Dema, in the ‘I am Clancy’ video:
Their authority comes from two things: a miraculous power and a hijacked religion. One feeds the other. A cycle. It’s called Vialism, and all you really need to know is that it teaches that self-destruction is the only way to paradise.

Some people think that Vialism means Weilism, after the Weil siblings Andre and Simone.
Simone Weil (1909-1943) was a French philosopher and political activist. In her later years she became increasingly religious and inclined towards mysticism.
Andre Weil (1906-1998) was a French mathematician and founding member of the Bourbaki group.

They enter the lore via a picture on Tyler Joseph’s desktop in the Zane Lowe interview in 2018, which is an overlay of two photographs of Bourbaki meetings in 1937 and 1938 featuring Andre and Simone.
For Simone this is the crucial period in her conversion to Catholicism, for Andre these meetings led to a reformulation of the foundations of TOPology, and discussions on Bourbaki’s version of Set theory which would lead to Bourbaki’s first book, published in 1939.
Both topics left a lasting impression on Simone Weil, as she wrote in 1942:
One field of mathematics that deals with all the diverse sorts of orders (set theory and general topology) is a treasure-house that holds an infinity of valuable expressions that show supernatural truth.
Now, Simone was fairly generous in her use of the adjective ‘supernatural’. Here’s another quote:
“The supernatural greatness of Christianity lies in the fact that it does not seek a supernatural remedy for suffering but a supernatural use for it.”
This suggests that if Vialism really is Weilism, then the ‘miraculous power’ might be mathematics (or at least the topics of set theory and topology), and the ‘hijacked religion’ might be the (ab)use of mathematics in theology.
Roughly speaking, axiomatic Zermelo-Fraenkel set theory gives a precise list of instructions to construct all sets out of two given sets, the empty set $\emptyset$ (the set containing nothing) being one of them.
Emptiness, or the void, is important in Simone Weil’s theology, see for example her book Love in the void: where God finds us

or consider this quote by her:
God stripped himself of his godhood and became empty, and fulfilled us with false godhood. Let us strip off this false godhood and become empty. This very act is the ultimate purpose to creating us.
which sounds a lot like Vialism, becoming an ’empty vessel’ for the Bishops (or God) to fill.
Also in 21 pilots’ iconography, the empty set $\emptyset$ is important.

Btw. the symbol $\emptyset$ for the empty set was first used by Andre Weil who remembered the Norwegian ‘eu’ from his studies of nordic languages preparing for his ‘Finnish fugue’ in 1939.
The other pre-given set challenges the Gods and theology. The Axiom of Infinity in the Zermelo-Fraenkel system asserts the existence of an infinite set, usually denoted $\omega$ and interpreted as the set of all finite numbers $\{ 0,1,2,3,4,5,6,\dots \}$.
In other words, mathematical set theory contains an object which is actual infinity!
From the ancient Greeks on to early modern times, philosophers adhered to the motto “Infinitum actu non datur”, there is only a potential infinity (the idea of infinity) but actual infinity belongs to the realm of the Gods (infinite power, infinite wisdom,…).
As if this was not heretic enough, in comes Georg Cantor.

Georg Cantor (1845-1918) might very well be another Clancy.
He was a German mathematician, discoverer of the secrets of infinity, which brought him in conflict with several influential mathematicians in his time (notably Kronecker and Poincare), and inventor of Cardinal numbers (compare Bishops).
He suffered from depression and mental illness, was often admitted to the Halle nerve clinic. In between he was a founding member of the DEutscher MAthematiker Vereinigung (DeMa) of which he was the first president (Nico), he suffered from malnourishment during WW1 (compare Simone Weil in WW2) and died of a heart attack in the sanatorium where he had spent the last year of his life.
Cantor showed that the only distinguishing feature between two sets is their Cardinality (Bishopy power), roughly speaking the number of things they contain. He then showed that for every set of a certain Bishopy power, there’s one of even higher power!
For example, there exists a set with higher cardinality than $\omega$, that is, a set we cannot enumerate. An example is described in these lines from Morph
Lights they blink to me, transmitting things to me
Ones and zeroes, ergo this symphony
Anybody listening? Ones and zeroes
Count to infinity, ones and zeroes
They’re talking about all possible infinite series of $0$’s and $1$’s and one quickly proves that these cannot be enumerated using Cantor’s diagonal argument.
When applied to theology this says that Gods cannot have any actual infinity power, for there’s always an entity posessing higher powers.
That’s why Cantor resolved to God being ‘absolute infinity’, the Bishopy power of the class of all cardinal numbers (emphasis only important for mathematicians).
Much more on the interplay between Cantor’s mathematical results on infinities and his theological writings can be found in the paper Absolute Infinity: � A Bridge Between Mathematics and Theology? by Christian Tapp.
The compassionate God of Christianity has presented theologians for centuries with the following paradox: how can a God having infinite power suffer because humans suffer?
In comes TOPology and one of its founding fathers Felix Hausdorff.

Felix Hausdorff (1868-1942) might very well be another Clancy.
He was a German mathematician who made substantial contributions to topology as well as set theory. For years he felt opposition because he was Jewish.
After the Kristallnacht in 1938 he tried to escape Nazi-Germany (DeMa) but couldn’t obtain a position in the US. On 26 January 1942, Felix Hausdorff, along with his wife and his sister-in-law, died by suicide, rather than comply with German orders to move to the Endenich camp.
He was also a philosopher and writer under the pseudonym Paul Mongré. In 1900 he wrote a book of poems, Ecstasy, of which the first poem is “Den Ungeflügelten” (To The Wingless Ones). Am I the only one to think immediately of The isle of the flightless birds?
Anyway, as to how the topology of Weilism solves the contradiction of the suffering God of Christianity is explained in the paper The Theology of Simone Weil and the Topology of Andre Weil by Ochiai Hitoshi, professor of ‘Mathematical Theology’ at Doshisha University, Kyoto.
He has a follow-up post Incarnation and Reincarnation on the Apeiron Centre (where he also has a post on the Theology of Georg Cantor). Here’s a summary of his thesis:
God is Open
Incarnation is Compactified God
The soul is Open
Reincarnation is Compactified Soul
God and the Soul are Homeomorphic
God is without Boundaries
The soul is with Boundaries
God and the Soul are not Diffeomorphic
This succinctly sums up Weilism for you.
I now understand why so many people in the 21 pilots sub-Reddit thought at the beginning of the Trench-era that Bourbaki was a group of mathematicians trying to prove the existence of God.
In the paper The Theology of Simone Weil and the Topology of Andre Weil the next quote is falsely attributed to Bourbaki
God is the Alexandroff compactification of the universe.
If you are interested in the history behind this quote you may read my post According to Groth. IV.22.
If you want an alternative explanation of Vialism, you may read my post Where’s Bourbaki’s Dema?.
Btw. I forgot to mention in that post the “Annual Assemblage of the Glorified”. Since 1918 this takes place November 11th, on Armistice Day.
In this series: