 Conjugacy classes of finite index subgroups of the modular group $\Gamma = PSL_2(\mathbb{Z}) $ are determined by a combinatorial gadget : a modular quilt. By this we mean a finite connected graph drawn on a Riemann surface such that its vertices are either black or white. Moreover, every edge in the graph connects a black to a white vertex and the valency (that is, the number of edges incodent to a vertex) of a black vertex is either 1 or 2, that of a white vertex is either 1 or 3. Finally, for every white vertex of valency 3, there is a prescribed cyclic order on the edges incident to it.
Conjugacy classes of finite index subgroups of the modular group $\Gamma = PSL_2(\mathbb{Z}) $ are determined by a combinatorial gadget : a modular quilt. By this we mean a finite connected graph drawn on a Riemann surface such that its vertices are either black or white. Moreover, every edge in the graph connects a black to a white vertex and the valency (that is, the number of edges incodent to a vertex) of a black vertex is either 1 or 2, that of a white vertex is either 1 or 3. Finally, for every white vertex of valency 3, there is a prescribed cyclic order on the edges incident to it.
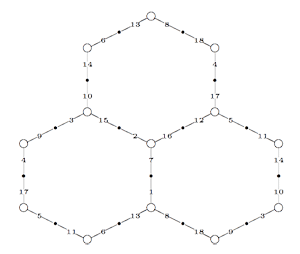
On the left a modular quilt consisting of 18 numbered edges (some vertices and edges re-appear) which gives a honeycomb tiling on a torus. All white vertices have valency 3 and the order of the edges is given by walking around a point in counterclockwise direction. For example, the order of the edges at the top left vertex (which re-appears at the middle right vertex) can be represented by the 3-cycle (6,11,14), that around the central vertex gives the 3-cycle (2,7,16).
As we will see _another time_, the modular group $\Gamma $ is freely generated by the two elements
$U=\begin{bmatrix} 0 & 1 \\\ -1 & 0 \end{bmatrix}~\qquad~V=\begin{bmatrix} 1 & 1 \\\ -1 & 0 \end{bmatrix} $
and remark that $U^2=V^3=1 $. To a modular quilt having d edges we can associate a transitive permutation representation of $\Gamma $ on d letters (the labels of the edges) such that the action of U is given by the order two permutation given by the product of all 2-cycles of incident edges to black 2-valent vertices and the action of V is given by the order three permutation given by the cyclic ordering of edges around white 3-valent vertices in the quilt. For the example above we have
$U \rightarrow (1,7)(2,15)(3,9)(4,17)(5,11)(6,13)(8,18)(10,14)(12,16) $
$V \rightarrow (1,13,8)(2,7,16)(3,15,10)(4,9,18)(5,17,12)(6,11,14) $
The (index d) subgroup of $\Gamma $ corresponding to the modular quilt is then the stabilizer subgroup of a fixed edge. Note that choosing a different edge gives a conjugate subgroup. Conversely, given an index d subgroup G we can label the d left-cosets in $\Gamma/G $ by the numbers 1,2,…,d and describe the action of left multiplication by U and V on the cosets as permutations in the symmetric group $S_d $. Because U has order two, its permutation will be a product of two cycles which we can interprete as giving the information on edges incident to 2-valent black vertices. Similarly, V has order three and hence its permutation consists of 3-cycles giving the ordering of edges around 3-valent white vertices. Edges not appearing in U (resp. V) have as their leaf-vertex a black (resp. white) vertex of valency 1. Because the permutation action is transitive, this procedure gives a connected graph on d edges, d white and d black vertices and is a modular quilt.
In order to connect modular quilts to special hyperbolic polygons we need the intermediate concept of cuboid tree diagrams. These are trees (that is, connected graphs without cycles) such that all internal vertices are 3-valent (and have an order on the incident edges) and the leaf-vertices are tinted either red or blue. In addition, there is an involution on the red vertices.
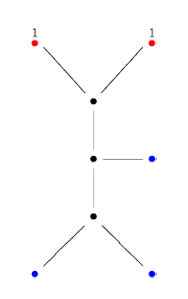
 The tree on the left is a cuboid tree, the involution interchanges the two top red vertices (indicated by having the same number). We associate to such a cuboid tree diagram a modular quilt by taking as the white vertices : all internal vertices together with the blue leaf-vertices, and as the black vertices : the midpoints of internal edges, together with the midpoints of edges connecting a blue leaf-vertex, together will all red leaf-vertices. If two red leaf-vertices correspond under the involution, we glue the corresponding black vertices together. That is, the picture of the right is the resulting modular quilt. Conversely, starting with a modular quilt we can always construct from it a cuboid tree diagram by breaking cycles in black vertices until there are no cycles left. All black leaf-vertices in the resulting tree are tinted red and correspond under the involution when they came from the same black quilt-vertex. Remaining leaf-vertices are tinted blue. All internal black vertices are removed (and the edges incident to them glued into larger edges) and all internal white vertices become the internal vertices of the cuboid tree.
The tree on the left is a cuboid tree, the involution interchanges the two top red vertices (indicated by having the same number). We associate to such a cuboid tree diagram a modular quilt by taking as the white vertices : all internal vertices together with the blue leaf-vertices, and as the black vertices : the midpoints of internal edges, together with the midpoints of edges connecting a blue leaf-vertex, together will all red leaf-vertices. If two red leaf-vertices correspond under the involution, we glue the corresponding black vertices together. That is, the picture of the right is the resulting modular quilt. Conversely, starting with a modular quilt we can always construct from it a cuboid tree diagram by breaking cycles in black vertices until there are no cycles left. All black leaf-vertices in the resulting tree are tinted red and correspond under the involution when they came from the same black quilt-vertex. Remaining leaf-vertices are tinted blue. All internal black vertices are removed (and the edges incident to them glued into larger edges) and all internal white vertices become the internal vertices of the cuboid tree.
While a cuboid tree diagram determines the modular quilt uniquely, there are in general several choices of breaking up cycles in a modular quilt, so also several cuboid tree diagrams determining the same modular quilt. That is, we have shown that there are natural maps
cuboid tree —->> modular quilt <----> conjugacy class of finite index subgroup
where the first map is finite to one and the second map is a bijection.
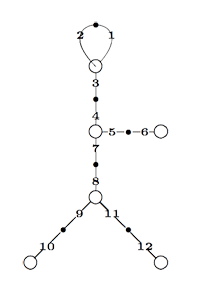
Observe that we can also use modular quilts (or their associated cuboid trees) as a mnemotechnic device to remember the construction of groups, generated by an order two and an order three element and having a low dimensional faithful permutation representation. For example, the sporadic simple Mathieu group $M_{12} $ has a 12-dimensional permutation representation encoded by the above left quilt, which we call the M(12) quilt. That is, $M_{12} $ is generated by the two permutations
(1,2)(3,4)(5,6)(7,8)(9,10)(11,12) and (1,2,3)(4,7,5)(8,9,11)
Hence the cuboid tree on the right can be called the M(12) tree. Similarly, the sporadic simple Mathieu group $M_{24} $ has a 24-dimensional permutation representation which can be represented by the modular quilt, the M(24) quilt
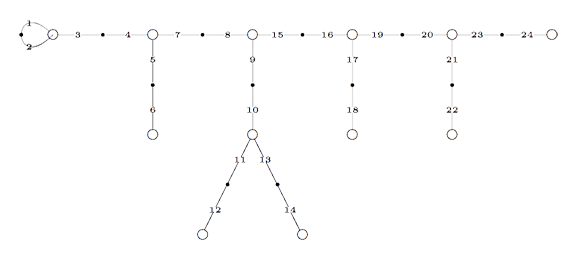
That is, $M_{24} $ is generated by the permutations (1,2,3)(4,5,7)(8,9,15)(10,11,13)(16,17,19)(20,21,23) and
(1,2)(3,4)(5,6)(7,8)(9,10)(11,12)(13,14)(15,16)(17,18)(19,20)(21,22)(23,24) with corresponding M(24) tree
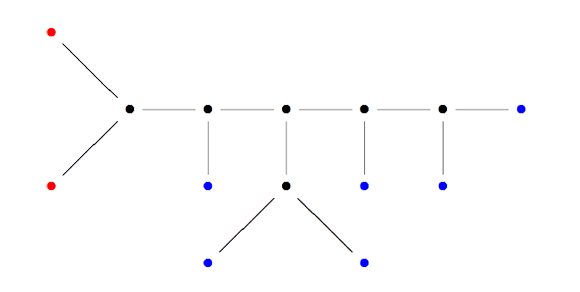
with the two red vertices interchanging under the involution.
References
Tim Hsu, “Permutation techniques for cosed representations of modular subgroups”
Ravi S. Kulkarni, “An arithmetic-geometric method in the study of the subgroups of the modular group” Amer. J. Math. 113 (1991) 1053-1133
4 Comments