Recently, I’ve been playing with the idea of writing a book for the general public. Its title is still unclear to me (though an idea might be “The disposable science”, better suggestions are of course wellcome) but I’ve fixed the subtitle as “Mathematics’ puzzling fall from grace”. The book’s concept is simple : I would consider the mathematical puzzles creating an hype over the last three centuries : the 14-15 puzzle for the 19th century, Rubik’s cube for the 20th century and, of course, Sudoku for the present century.
For each puzzle, I would describe its origin, the mathematics involved and how it can be used to solve the puzzle and, finally, what the differing quality of these puzzles tells us about mathematics’ changing standing in society over the period. Needless to say, the subtitle already gives away my point of view. The final part of the book would then be more optimistic. What kind of puzzles should we promote for mathematical thinking to have a fighting chance to survive in the near future?
 One of the puzzles I would propose is $M_{13} $, a sliding game first proposed by John Horton Conway in 1989 at the fourteenth New York Graph Theory Day. The analysis of the game was taken up by Jeremy Martin in his 1996 honors thesis in mathematics The Mathieu group M(12) and Conway’s M(13)-game under the supervision of Noam Elkies.
One of the puzzles I would propose is $M_{13} $, a sliding game first proposed by John Horton Conway in 1989 at the fourteenth New York Graph Theory Day. The analysis of the game was taken up by Jeremy Martin in his 1996 honors thesis in mathematics The Mathieu group M(12) and Conway’s M(13)-game under the supervision of Noam Elkies.
Two years ago, the three of them joined forces and arXived the paper The Mathieu group M(12) and its pseudogroup extension M(13). The game is similar to the 15-puzzle replacing the role played by the simple alternating group $A_{15} $ there with that of the sporadic simple Mathieu group $M_{12} $.
The game board of $M_{13} $ is the finite projective plane $\mathbb{P}^2(\mathbb{F}_3) $ over the field with three elements $\mathbb{F}_3 $. Recall that the number of points in projective n-space over a finite field of q-elements $\mathbb{P}^n(\mathbb{F}_q) $ is given by
$ q^n + q^{n-1} + \cdots + q + 1 $
Therefore, there are 13=9+3+1 points on the board and as there is a bijection between points and lines in the projective plane, there are also 13 lines on the board, each containing exactly 4=3+1 points and so each point lies on exactly 4 lines.
Moreover, two distinct points p and q determine a unique line $\overline{pq} $ and two distinct lines l and m have a unique intersection point $l \cap m = { p } $. Clearly it will be hard selling a projective plane board to the general public, so let us depict all this information in a more amenable form such as
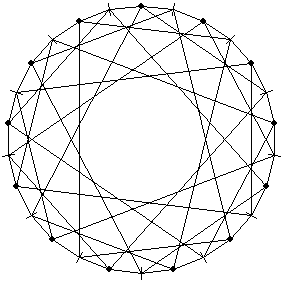
The 13 points are indicated by the small discs around the circle whereas the 13 lines are depicted as small strokes on the circle. All edges (both ‘along’ as well ‘inside’ the circle) connect a point p and a line l subject to the relation that p lies on the line l in the projective plane $\mathbb{P}^2(\mathbb{F}_3) $.
The fact that two distinct points determine a unique line corresponds to the fact that for any two small-discs there is a unique small-stroke connecting both small-discs with an edge (note that one or both of these edges may lie on the circle). Similarly, for any two small-strokes the is a unique small-disc connected via edges to the two small-strokes, corresponding to the fact that two lines have a unique point in common.
A typical position in Conway’s puzzle $M_{13} $ consists in placing numbered counters, labeled 1 through 12, on 12 of the 13 points leaving one point empty, called the “hole”. A basic move consists of the following operation : choose a labeled point, say, p. Then, there is a unique line l (a small-stroke) containing p and the hole and there are two more points say q and r on this line l. The basic move replaces the counters between q and r and moves the counter of p to the hole and the hole to point p. For example, consider the position on the left
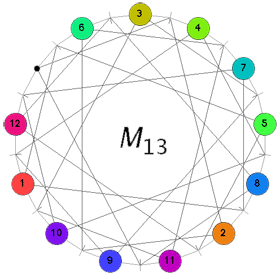
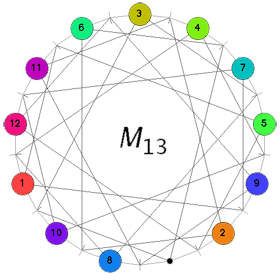
and suppose we want to move the counter 11 to the hole. Hole and 11 determine the unique line represented by the small-stroke immediately to the left of 11. This line contains the further points with counters 8 and 9. Hence, applying the basic move we get the situation on the right hand side. The aim of Conway’s game M(13) is to get the hole at the top point and all counters in order 1,2,…,12 when moving clockwise along the circle. One can play this puzzle online using the excellent java-applet by Sebastian Egner.
Another time we will make the connection with the Mathieu groupoid M(13) and the sporadic simple Mathieu group $M_{12} $.
Reference
John H. Conway, Noam D. Elkies, and Jeremy L. Martin “The Mathieu group M(12) and its pseudogroup extension M(13)”
Comments