A fun way to teach first year students the different methods of proof is to play a game with chocolate bars, Chomp.
The players take turns to choose one chocolate block and “eat it”, together with all other blocks that are below it and to its right. There is a catch: the top left block contains poison, so the first player forced to eat it dies, that is, looses the game.
Let’s prove some results about Chomp illustrating the strengths and weaknesses of different methods of proof.
[section_title text=”Direct proof”]
By far the most satisfying method is the ‘direct proof’. Once you understand it, the truth of the statement is unescapable.
Theorem 1: The first player to move has a winning strategy for a $2 \times n$ chocolate bar.
Here’s the winning move: you take the lower right block!

What can the other player do? She can bring the bar again in rectangular shape of strictly smaller size (in which case you eat again the lower right block), or she can eat more blocks from the lower row (but then, after her move, you eat as many blocks from the top row bringing the bar again in a shape in which the top row has exactly one more block than the lower one. You’re bound to win!
Sadly, it is not always possible to prove what you want in such a direct way. That’s why we invented another tactic:
[section_title text=”Proof by induction”]
A proof by induction is less satisfactory because it involves a lot more work, but still everyone considers it as a ‘fair’ method: it shows how to arrive at the solution, if only you had enough time and energy…
Theorem 2: Given any Chomp position, either the first player to move has a winning strategy or the second player has one.
A proof by induction relies on simplifying the situation at hand. Here, each move reduces the number of blocks in the chocolate bar, so we can apply induction on the number of blocks.
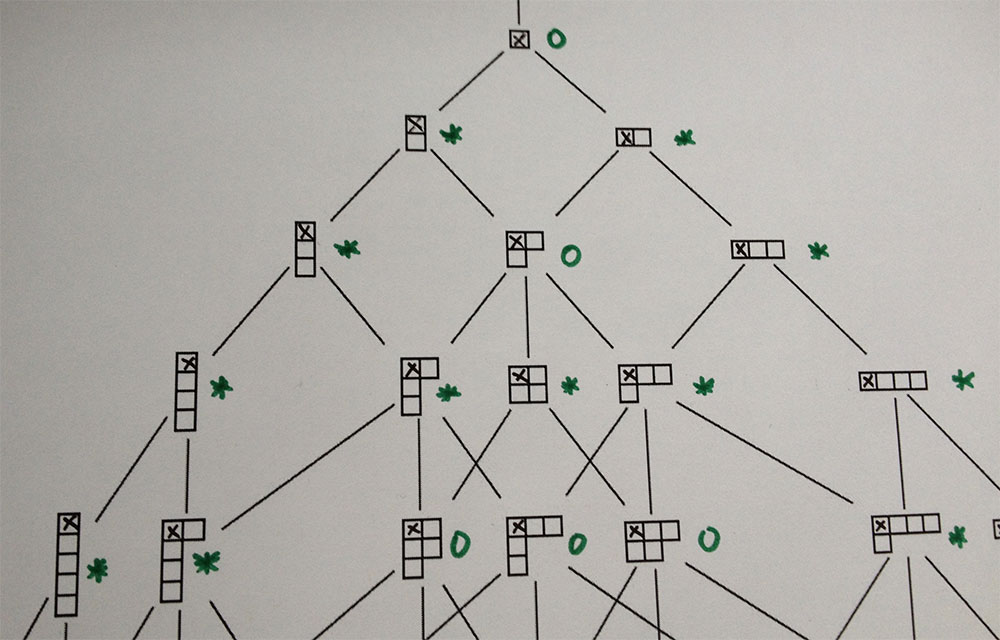
If there is just one block, it must contain poison and so the first player has to eat it and looses the game. That is, here the second player has a winning strategy and we indicate this by labelling the position with $0$. This one block position is the ‘basis’ for our induction.
Now, take a position $P$ for which you want to prove the claim. Look at all possible positions $X$ you get after one move. All these positions have strictly less blocks, so ‘by induction’ we may assume that the result is true for each one of them. So we can label each of these positions with $0$ if it is a second player win, or with $\ast$ if it is a first player win.
How to label $P$? Well, if all positions in $X$ are labeled $\ast$ we label $P$ with $0$ because it is a second player win. The first player has to move to a starred position (which is a first player win) and so the second player has a winning strategy from it (by moving to a $0$-position). If there is at least one position in $X$ labeled $0$ then we label $P$ with $\ast$. Indeed, the first player can move to the $0$-position and then has a winning strategy, playing second.
Here’s the chart of the first batch of positions:
But then, it may take your lifetime to work through the strategy for a complicated starting position…
What to do if neither a direct proof is found, nor a reduction argument allowing a proof by induction? Virtually all professional mathematicians have no objection whatsoever to resort to a very drastic tactic: proof by contradiction.
[section_title text=”Proof by contradiction”]
The law of the excluded third (or ‘tertium non datur’) says that for any proposition $P$ either $P$ or not $P$ is true. In 1927 David Hilbert stated that not much of mathematics would remain without the use of this rule:
[quote name=”David Hilbert”]To prohibit existence statements and the principle of excluded middle is tantamount to relinquishing the science of mathematics altogether.[/quote]
Theorem 3: The first player has a winning strategy for a rectangular starting position.
We will prove this by contradiction. That is, we will assume that it is false, that is, the first player has not a winning strategy, and derive a contradiction from it. Therefore $\neg \neg P$ is true which is equivalent to $P$ by the law of the excluded
middle.
If the first player does not have a winning strategy for that rectangular chocolate bar, the second player must have one by Theorem2. That is, for every possible first move the second player has a winning response.
Assume the first player eats the lower right block.

The second player must have some winning response to this. Whatever her move, the resulting position could have been obtained by the first player already after the first move.

So, the second player cannot have a winning strategy.
This strategy stealing argument is a cheap cheat. We have not the slightest idea of what the winning strategy for the first player is or how to find it.
Still, one shouldn’t stress this fact too much to first year students. They’ll have to work through plenty of proofs by contradiction in the years ahead…
[section_title text=”Accepting constructive mathematics?”]
Sooner or later in their career they will hear arguments in favour of ‘constructive mathematics’, which does not accept the law of the excluded third.
Andrej Bauer has described was happens next. They will go through the five stages people need to come to terms with life’s traumatising events: denial, anger, bargaining, depression, and finally acceptance.
His paper is just out in the Bulletin of the AMS Five stages of accepting constructive mathematics.
This paper is an extended version of a talk he gave at the IAS.

Theorem 3 fails in the 1×1 case!