Following up on the deep learning and toposes-post, I was planning to do something on the logic of neural networks.
Prepping for this I saw David Spivak’s paper Learner’s Languages doing exactly that, but in the more general setting of ‘learners’ (see also the deep learning post).
And then … I fell under the spell of $\mathbf{Poly}$.
Spivak is a story-telling talent. A long time ago I copied his short story (actually his abstract for a talk) “Presheaf, the cobbler” in the Children have always loved colimits-post.
Last week, he did post Poly makes me happy and smart on the blog of the Topos Institute, which is another great read.
If this is way too ‘fluffy’ for you, perhaps you should watch his talk Poly: a category of remarkable abundance.
If you like (applied) category theory and have some days to waste, you can binge-watch all 15 episodes of the Poly-course Polynomial Functors: A General Theory of Interaction.
If you are more the reading-type, the 273 pages of the Poly-book will also kill a good number of your living hours.
Personally, I have no great appetite for category theory, I prefer to digest it in homeopathic doses. And, I’m allergic to co-terminology.
So then, how to define $\mathbf{Poly}$ for the likes of me?
$\mathbf{Poly}$, you might have surmised, is a category. So, we need ‘objects’ and ‘morphisms’ between them.
Any set $A$ has a corresponding ‘representable functor’ sending a given set $S$ to the set of all maps from $A$ to $S$
\[
y^A~:~\mathbf{Sets} \rightarrow \mathbf{Sets} \qquad S \mapsto S^A=Maps(A,S) \]
This looks like a monomial in a variable $y$ ($y$ for Yoneda, of course), but does it work?
What is $y^1$, where $1$ stands for the one-element set $\{ \ast \}$? $Maps(1,S)=S$, so $y^1$ is the identity functor sending $S$ to $S$.
What is $y^0$, where $0$ is the empty set $\emptyset$? Well, for any set $S$ there is just one map $\emptyset \rightarrow S$, so $y^0$ is the constant functor sending any set $S$ to $1$. That is, $y^0=1$.
Going from monomials to polynomials we need an addition. We add such representable functors by taking disjoint unions (finite or infinite), that is
\[
\sum_{i \in I} y^{A_i}~:~\mathbf{Sets} \rightarrow \mathbf{Sets} \qquad S \mapsto \bigsqcup_{i \in I} Maps(A_i,S) \]
If all $A_i$ are equal (meaning, they have the same cardinality) we use the shorthand $Iy^A$ for this sum.
The objects in $\mathbf{Poly}$ are exactly these ‘polynomial functors’
\[
p = \sum_{i \in I} y^{p[i]} \]
with all $p[i] \in \mathbf{Sets}$. Remark that $p(1)=I$ as for any set $A$ there is just one map to $1$, that is $y^A(1) = Maps(A,1) = 1$, and we can write
\[
p = \sum_{i \in p(1)} y^{p[i]} \]
An object $p \in \mathbf{Poly}$ is thus described by the couple $(p(1),p[-])$ with $p(1)$ a set, and a functor $p[-] : p(1) \rightarrow \mathbf{Sets}$ where $p(1)$ is now a category with objects the elements of $p(1)$ and no morphisms apart from the identities.
We can depict $p$ by a trimmed down forest, Spivak calls it the corolla of $p$, where the tree roots are the elements of $p(1)$ and the tree with root $i \in p(1)$ has one branch from the root for any element in $p[i]$. The corolla of $p=y^2+2y+1$ looks like
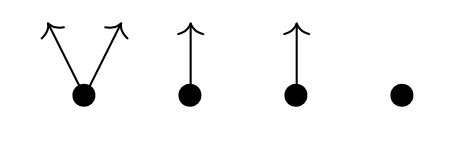
If $M$ is an $m$-dimensional manifold, then you might view its tangent bundle $TM$ set-theoretically as the ‘corolla’ of the polynomial functor $M y^{\mathbb{R}^m}$, the tree-roots corresponding to the points of the manifold, and the branches to the different tangent vectors in these points.
Morphisms in $\mathbf{Poly}$ are a bit strange. For two polynomial functors $p=(p(1),p[-])$ and $q=(q(1),q[-])$ a map $p \rightarrow q$ in $\mathbf{Poly}$ consists of
- a map $\phi_1 : p(1) \rightarrow q(1)$ on the tree-roots in the right direction, and
- for any $i \in p(1)$ a map $q[\phi_1(i)] \rightarrow p[i]$ on the branches in the opposite direction
In our manifold/tangentbundle example, a morphism $My^{\mathbb{R}^m} \rightarrow y^1$ sends every point $p \in M$ to the unique root of $y^1$ and the unique branch in $y^1$ picks out a unique tangent-vector for every point of $M$. That is, vectorfields on $M$ are very special (smooth) morphisms $Mu^{\mathbb{R}^m} \rightarrow y^1$ in $\mathbf{Poly}$.
A smooth map between manifolds $M \rightarrow N$, does not determine a morphism $My^{\mathbb{R}^m} \rightarrow N y^{\mathbb{R}^n}$ in $\mathbf{Poly}$ because tangent vectors are pushed forward, not pulled back.
If instead we view the cotangent bundle $T^*M$ as the corolla of the polynomial functor $My^{\mathbb{R}^m}$, then everything works well.
But then, I promised not to use co-terminology…
Another time I hope to tell you how $\mathbf{Poly}$ helps us to understand the logic of learners.
Leave a Comment