I was hoping you would write a post on the ‘uninteresting case’ of p=5 in this context. Note that the truncated tetrahedron has (V,E,F)=(12,18,8) which is a triple that appears in the ternary (cyclic) geometry for the cube. This triple can be 4 hexagons and 4 triangles (the truncated tetrahedron) OR 4 pentagons and 4 squares!
Kea commented and I didnt know the answer to the ‘obvious’ question :
how can one get the truncated tetrahedron from either of the two conjugacy classes of order 5 elements in $L_2(5)=A_5 $, each consisting of 12 elements.
Fortunately the groups involved are small enough to enable hand-calculations. Probably there is a more elegant way to do this, but I was already happy to find this construction…
This time, there is just one conjugacy class of subgroups isomorphic to $A_4 $ (the symmetry group of the (truncated) tetrahedron) in $L_2(5)=A_5 $. Take one of the two conjugacy classes C of 5-cycles in $A_5 $ and use the following notation for its 12 elements :
A=(1,2,3,4,5), B=(1,2,4,5,3), C=(1,2,5,3,4), D=(1,3,5,4,2), E=(1,3,2,5,4), F=(1,3,4,2,5), G=(1,5,4,3,2), H=(1,5,3,2,4), I=(1,5,2,4,3), J=(1,4,2,3,5), K=(1,4,5,2,3), L=(1,4,3,5,2)
We’d like to view these elements as the vertices of a truncated tetrahedron, so we need to find the 4 triangles and the 6 connecting edges between them. The first task calls for order 3 elements, the second one for order two elements.
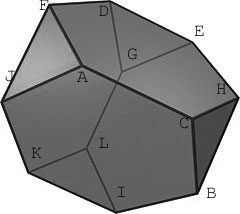Take a conjugacy class of order 3 elements in $A_4 $ say $T={ (2,4,3),(1,2,3),(1,3,4),(1,4,2) } $ and observe that when one computes the products of T with a fixed 5-cycle in the conjugacy class C there is a unique element among the four obtained that belongs to the conjugacy class C. This gives a cyclic action on C with orbits of length 3 (the triangles). Here they are :
A–> J –> F –> A, B–>C–>H–>B, D–>G –> E–>D, I–>L–>K–>I
For the edges, take the conjugacy class $S= { (1,2)(3,4),(1,3)(2,4),(1,4)(2,3) } $ of order two elements in $A_4 $ and compute for any 5-cycle c in C the products c_S_c and observe that among the elements obtained there is again one element belonging to C. This gives the following pairing
A<-->C, B<-->I, D<-->F, E<-->H, G<-->L and J<-->K and a bit of puzzling shows that all this can indeed be realized within a truncated tetrahedron (on the right). As to her other request
… and how about a post on how 1 + 4 + 9 + … + 24^2 = 70^2 is REALLY a statement about unifying cusps and holes (genus) as degrees of freedom in quantum geometry.
The scarecrow will need to take some time to think before giving his answer…
One Comment