Here I will go over the last post at a more leisurely pace, focussing on a couple of far more trivial examples. Here’s the goal : we want to assign a quiver-superpotential to any subgroup of finite index of the modular group. So fix such a subgroup $\Gamma’ $ of the modular group $\Gamma=PSL_2(\mathbb{Z}) $ and consider the associated permutation representation of $\Gamma $ on the left-cosets $\Gamma/\Gamma’ $. As $\Gamma \simeq C_2 \ast C_3 $ this representation is determined by the action of the order 2 and order 3 generators of the modular group. There are a number of combinatorial gadgets to control the subgroup $\Gamma’ $ and the associated permutation representation : (generalized) Farey symbols and dessins d’enfants.
Recall that the modular group acts on the upper-halfplane (the ‘hyperbolic plane’) by Moebius transformations, so to any subgroup $\Gamma’ $ we can associate a fundamental domain for its restricted action. The dessins and the Farey symbols give us a particular choice of these fundamental domains. Let us consider the two most trivial subgroups of all : the modular group itself (so $\Gamma/\Gamma $ is just one element and therefore the associated permutation representation is just the trivial representation) and the unique index two subgroup $\Gamma_2 $ (so there are two cosets $\Gamma/\Gamma_2 $ and the order 2 generator interchanges these two while the order 3 generator acts trivially on them). The fundamental domains of $\Gamma $ (left) and $\Gamma_2 $ (right) are depicted below
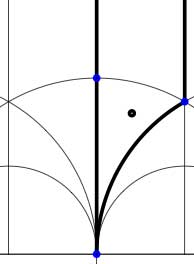
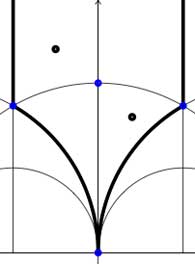
In both cases the fundamental domain is bounded by the thick black (hyperbolic) edges. The left-domain consists of two hyperbolic triangles (the upper domain has $\infty $ as the third vertex) and the right-domain has 4 triangles. In general, if the subgroup $\Gamma’ $ has index n, then its fundamental domain will consist of $2n $ hyperbolic triangles. Note that these triangles are part of the Dedekind tessellation so really depict the action of $PGL_2(\mathbb{Z} $ and any $\Gamma $-hyperbolic triangle consists of one black and one white triangle in Dedekind’s coloring. We will indicate the color of a triangle by a black circle if the corresponding triangle is black. Of course, the bounding edges of the fundamental domain need to be identified and the Farey symbol is a notation device to clarify this. The Farey symbols of the above domains are
[tex]\xymatrix{\infty \ar@{-}[r]_{\circ} & 0 \ar@{-}[r]_{\bullet} & \infty}[/tex] and [tex]\xymatrix{\infty \ar@{-}[r]_{\bullet} & 0 \ar@{-}[r]_{\bullet} & \infty}[/tex] respectively. In both cases this indicates that the two bounding edges on the left are to be identified as are the two bounding edges on the right (so, in particular, after identification $\infty $ coincides with $0 $). Hence, after identification, the $\Gamma $ domain consists of two triangles on the vertices ${ 0,i,\rho } $ (where $\rho=e^{2 \pi i}{6} $) (the blue dots) sharing all three edges, the $\Gamma_2 $ domain consists of 4 triangles on the 4 vertices ${ 0,i,\rho,\rho^2 } $ (the blue dots). In general we have three types of vertices : cusps (such as 0 or $\infty $), even vertices (such as $i $ where there are 4 hyperbolic edges in the Dedekind tessellation) and odd vertices (such as $\rho $ and $\rho^2 $ where there are 6 hyperbolic edges in the tessellation).
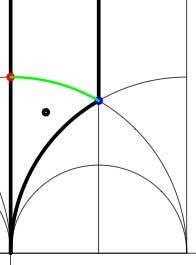
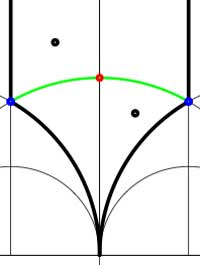Another combinatorial gadget assigned to the fundamental domain is the cuboid tree diagram or dessin. It consists of all odd and even vertices on the boundary of the domain, together with all odd and even vertices in the interior. These vertices are then connected with the hyperbolic edges connecting them. If we color the even vertices red and the odds blue we have the indicated dessins for our two examples (the green pictures). An half-edge is an edge connecting a red and a blue vertex in the dessin and we number all half-edges. So, the $\Gamma $-dessin has 1 half-edge whereas the $\Gamma_2 $-dessin has two (in general, the number of these half-edges is equal to the index of the subgroup). Observe also that every triangle has exactly one half-edge as one of its three edges. The dessin gives all information to calculate the permutation representation on the coset-set $\Gamma/\Gamma’ $ : the action of the order 2 generator of $\Gamma $ is given by taking for each internal red vertex the two-cycle $~(a,b) $ where a and b are the numbers of the two half-edges connected to the red vertex and the action of the order 3 generator is given by taking for every internal blue vertex the three cycle $~(c,d,e) $ where c, d and e are the numbers of the three half-edges connected to the blue vertex in counter-clockwise ordering. Our two examples above are a bit too simplistic to view this in action. There are no internal blue vertices, so the action of the order 3 generator is trivial in both cases. For $\Gamma $ there is also no red internal vertex, whence this is indeed the trivial representation whereas for $\Gamma_2 $ there is one internal red vertex, so the action of the order 2 generator is given by $~(1,2) $, which is indeed the representation representation on $\Gamma/\Gamma_2 $. In general, if the index of the subgroup $\Gamma’ $ is n, then we call the subgroup of the symmetric group on n letters $S_n $ generated by the action-elements of the order 2 and order 3 generator the monodromy group of the permutation representation (or of the subgroup). In the trivial cases here, the monodromy groups are the trivial group (for $\Gamma $) and $C_2 $ (for $\Gamma_2 $).
As a safety-check let us work out all these concepts in the next simplest examples, those of some subgroups of index 3. Consider the Farey symbols
[tex]\xymatrix{\infty \ar@{-}[r]_{\circ} & 0 \ar@{-}[r]_{\circ} & 1 \ar@{-}[r]_{\circ} & \infty}[/tex] and
[tex]\xymatrix{\infty \ar@{-}[r]_{\circ} & 0 \ar@{-}[r]_{1} & 1 \ar@{-}[r]_{1} & \infty}[/tex]
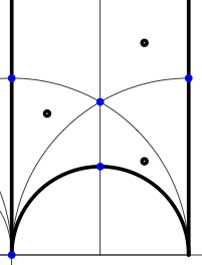
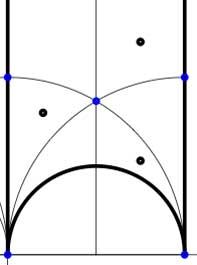In these cases the fundamental domain consists of 6 triangles with the indicated vertices (the blue dots). The distinction between the two is that in the first case, one identifies the two edges of the left, resp. bottom, resp. right boundary (so, in particular, 0,1 and $\infty $ are identified) whereas in the second one identifies the two edges of the left boundary and identifies the edges of the bottom with those of the right boundary (here, 0 is identified only with $\infty $ but also $1+i $ is indetified with $\frac{1}{2}+\frac{1}{2}i $).
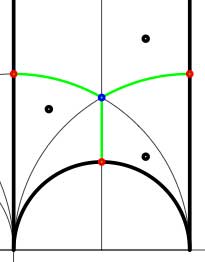In both cases the dessin seems to be the same (and given by the picture on the right). However, in the first case all three red vertices are distinct hence there are no internal red vertices in this case whereas in the second case we should identify the bottom and right-hand red vertex which then becomes an internal red vertex of the dessin!
Hence, if we order the three green half-edges 1,2,3 starting with the bottom one and counting counter-clockwise we see that in both cases the action of the order 3-generator of $\Gamma $ is given by the 3-cycle $~(1,2,3) $. The action of the order 2-generator is trivial in the first case, while given by the 2-cycle $~(1,2) $ in the second case. Therefore, the monodromy group is the cylic group $C_3 $ in the first case and is the symmetric group $S_3 $ in the second case.
Next time we will associate a quiver to these vertices and triangles as well as a cubic superpotential which will then allow us to define a noncommutative algebra associated to any subgroup of the modular group. The monodromy group of the situation will then reappear as a group of algebra-automorphisms of this noncommutative algebra!
One Comment