 Just as cartographers like
Just as cartographers like
Mercator drew maps of
the then known world, we draw dessins
d ‘enfants to depict the
associated algebraic curve defined over
$\overline{\mathbb{Q}} $.
In order to see that such a dessin
d’enfant determines a permutation representation of one of
Grothendieck’s cartographic groups, $SL_2(\mathbb{Z}),
\Gamma_0(2) $ or $\Gamma(2) $ we need to have realizations of these
groups (as well as their close relatives
$PSL_2(\mathbb{Z}),GL_2(\mathbb{Z}) $ and $PGL_2(\mathbb{Z}) $) in
terms of generators and relations.
As this lesson will be rather
technical I’d better first explain what we will prove (so that you can
skip it if you feel comfortable with the statements) and why we want to
prove it. What we will prove in detail below is that these groups
can be written as free (or amalgamated) group products. We will explain
what this means and will establish that
$PSL_2(\mathbb{Z}) = C_2
\ast C_3, \Gamma_0(2) = C_2 \ast C_{\infty}, \Gamma(2)
= C_{\infty} \ast C_{\infty} $
$SL_2(\mathbb{Z}) =
C_4 \ast_{C_2} C_6, GL_2(\mathbb{Z}) = D_4 \ast_{D_2} D_6,
PGL_2(\mathbb{Z}) = D_2 \ast_{C_2} D_3 $
where $C_n $ resp.
$D_n $ are the cyclic (resp. dihedral) groups. The importance of these
facts it that they will allow us to view the set of (isomorphism classes
of) finite dimensional representations of these groups as
noncommutative manifolds . Looking at the statements above we
see that these arithmetical groups can be build up from the first
examples in any course on finite groups : cyclic and dihedral
groups.
Recall that the cyclic group of order n, $C_n $ is the group of
rotations of a regular n-gon (so is generated by a rotation r with
angle $\frac{2 \pi}{n} $ and has defining relation $r^n = 1 $, where 1
is the identity). However, regular n-gons have more symmetries :
flipping over one of its n lines of symmetry
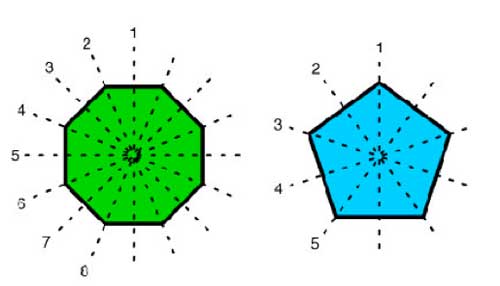
The dihedral group $D_n $ is the group generated by the n
rotations and by these n flips. If, as before r is a generating
rotation and d is one of the flips, then it is easy to see that the
dihedral group is generated by r and d and satisfied the defining
relations
$r^n=1 $ and $d^2 = 1 = (rd)^2 $
Flipping twice
does nothing and to see the relation $~(rd)^2=1 $ check that doing twice a
rotation followed by a flip brings all vertices back to their original
location. The dihedral group $D_n $ has 2n elements, the n-rotations
$r^i $ and the n flips $dr^i $.
In fact, to get at the cartographic
groups we will only need the groups $D_4, D_6 $ and their
subgroups. Let us start by finding generators of the largest
group $GL_2(\mathbb{Z}) $ which is the group of all invertible $2
\times 2 $ matrices with integer coefficients.
Consider the
elements
$U = \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix},
V = \begin{bmatrix} 0 & 1 \\ -1 & 1 \end{bmatrix}/tex] and $R =
\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} $
and form the
matrices
$X = UV = \begin{bmatrix} 1 & -1 \\ 0 & 1
\end{bmatrix}, Y = VU = \begin{bmatrix} 1 & 0 \\ 1 & 1
\end{bmatrix} $
By induction we prove the following relations in
$GL_2(\mathbb{Z}) $
$X^n \begin{bmatrix} a & b \\ c & d
\end{bmatrix} = \begin{bmatrix} a-nc & b-nd \\ c & d \end{bmatrix} $
and $\begin{bmatrix} a & b \\ c& d \end{bmatrix} X^n =
\begin{bmatrix} a & b-na \\ c & d-nc \end{bmatrix} $
$Y^n \begin{bmatrix} a & b \\ c & d \end{bmatrix} =
\begin{bmatrix} a & b \\ c+na & d+nb \end{bmatrix} $ and
$\begin{bmatrix} a & b \\ c & d \end{bmatrix} Y^n = \begin{bmatrix}
a+nb & b \\ c+nd & d \end{bmatrix} $
The determinant ad-bc of
a matrix in $GL_2(\mathbb{Z}) $ must be $\pm 1 $ whence all rows and
columns of
$\begin{bmatrix} a & b \\ c & d \end{bmatrix} \in
GL_2(\mathbb{Z}) $
consist of coprime numbers and hence a and
c can be reduced modulo each other by left multiplication by a power
of X or Y until one of them is zero and the other is $\pm 1 $. We
may even assume that $a = \pm 1 $ (if not, left multiply with U).
So,
by left multiplication by powers of X and Y and U we can bring any
element of $GL_2(\mathbb{Z}) $ into the form
$\begin{bmatrix}
\pm 1 & \beta \\ 0 & \pm 1 \end{bmatrix} $
and again by left
multiplication by a power of X we can bring it in one of the four
forms
$\begin{bmatrix} \pm 1 & 0 \\ 0 & \pm 1 \end{bmatrix}
= { 1,UR,RU,U^2 } $
This proves that $GL_2(\mathbb{Z}) $ is
generated by the elements U,V and R.
Similarly, the group
$SL_2(\mathbb{Z}) $ of all $2 \times 2 $ integer matrices with
determinant 1 is generated by the elements U and V as using the
above method and the restriction on the determinant we will end up with
one of the two matrices
${ \begin{bmatrix} 1 & 0 \\ 0 & 1
\end{bmatrix},\begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix} } =
{ 1,U^2 } $
so we never need the matrix R. As for
relations, there are some obvious relations among the matrices U,V and
R, namely
$U^2=V^3 $ and $1=U^4=R^2=(RU)^2=(RV)^2$ $
The
real problem is to prove that all remaining relations are consequences
of these basic ones. As R clearly has order two and its commutation
relations with U and V are just $RU=U^{-1}R $ and $RV=V^{-1}R $ we can
pull R in any relation to the far right and (possibly after
multiplying on the right with R) are left to prove that the only
relations among U and V are consequences of $U^2=V^3 $ and
$U^4=1=V^6 $.
Because $U^2=V^3 $ this element is central in the
group generated by U and V (which we have seen to be
$SL_2(\mathbb{Z}) $) and if we quotient it out we get the modular
group
$\Gamma = PSL_2(\mathbb{Z}) $
Hence in order to prove our claim
it suffices that
$PSL_2(\mathbb{Z}) = \langle
\overline{U},\overline{V} : \overline{U}^2=\overline{V}^3=1
\rangle $
Phrased differently, we have to show that
$PSL_2(\mathbb{Z}) $ is the free group product of the cyclic groups of
order two and three (those generated by $u = \overline{U} $ and
$v=\overline{V} $) $C_2 \ast C_3 $
Any element of this free group
product is of the form $~(u)v^{a_1}uv^{a_2}u \ldots
uv^{a_k}(u) $ where beginning and trailing u are optional and
all $a_i $ are either 1 or 2.
So we have to show that in
$PSL_2(\mathbb{Z}) $ no such word can give the identity
element. Today, we will first sketch the classical argument based
on the theory of groups acting on trees due to Jean-Pierre
Serre and Hyman Bass. Tomorrow, we will give a short elegant proof due to
Roger Alperin and draw
consequences to the description of the carthographic groups as
amalgamated free products of cyclic and dihedral groups.
Recall
that $GL_2(\mathbb{Z}) $ acts via Moebius
transformations on
the complex plane $\mathbb{C} = \mathbb{R}^2 $ (actually it is an
action on the Riemann sphere $\mathbb{P}^1_{\mathbb{C}} $) given by the
maps
$\begin{bmatrix} a & b \\ c & d \end{bmatrix}.z =
\frac{az+b}{cz+d} $
Note that the action of the
center of $GL_2(\mathbb{Z}) $ (that is of $\pm \begin{bmatrix} 1 & 0
\\ 0 & 1 \end{bmatrix} $) acts trivially, so it is really an action of
$PGL_2(\mathbb{Z}) $.
As R interchanges the upper and lower half-plane
we might as well restrict to the action of $SL_2(\mathbb{Z}) $ on the
upper-halfplane $\mathcal{H} $. It is quite easy to see that a
fundamental domain
for this action is given by the greyed-out area
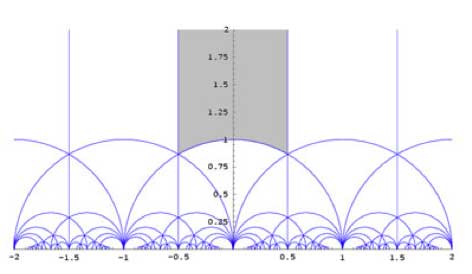
To see that any $z \in \mathcal{H} $ can be taken into this
region by an element of $PSL_2(\mathbb{Z}) $ note the following two
Moebius transformations
$\begin{bmatrix} 1 & 1 \\ 0 & 1
\end{bmatrix}.z = z+1 $ and $\begin{bmatrix} 0 & 1 \\ -1
& 0 \end{bmatrix}.z = -\frac{1}{z} $
The first
operation takes any z into a strip of length one, for example that
with Re(z) between $-\frac{1}{2} $ and $\frac{1}{2} $ and the second
interchanges points within and outside the unit-circle, so combining the
two we get any z into the greyed-out region. Actually, we could have
taken any of the regions in the above tiling as our fundamental domain
as they are all translates of the greyed-out region by an element of
$PSL_2(\mathbb{Z}) $.
Of course, points on the boundary of the
greyed-out fundamental region need to be identified (in order to get the
identification of $\overline{\mathcal{H}/PSL_2(\mathbb{Z})} $ with the
Riemann sphere $S^2=\mathbb{P}^1_{\mathbb{C}} $). For example, the two
halves of the boundary by the unit circle are interchanged by the action
of the map $z \rightarrow -\frac{1}{z} $ and if we take the translates under
$PSL_2(\mathbb{Z}) $ of the indicated circle-part
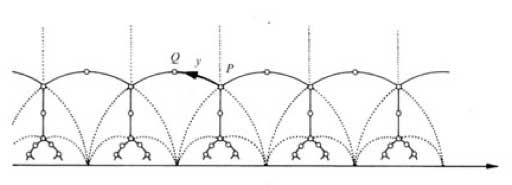
we get a connected tree with fundamental domain the circle
part bounded by i and $\rho = \frac{1}{2}+\frac{\sqrt{3}}{2} i $.
Calculating the stabilizer subgroup of i (that is, the subgroup of
elements fixing i) we get that this subgroup
is $\langle u \rangle = C_2 $ whereas the stabilizer subgroup of
$\rho $ is $\langle v \rangle = C_3 $.
Using this facts and the general
results of Jean-Pierre Serres book Trees
one deduces that $PSL_2(\mathbb{Z}) = C_2 \ast C_3 $
and hence that the obvious relations among U,V and R given above do
indeed generate all relations.
4 Comments