Smith – neverendingbooks

On March 20th, David Smith, Joseph Myers, Craig Kaplan and Chaim Goodman-Strauss announced on the arXiv that they’d found an ein-Stein (a stone), that is, one piece to tile the entire plane, in uncountably many different ways, all of them non-periodic (that is, the pattern does not even allow a translation symmetry).

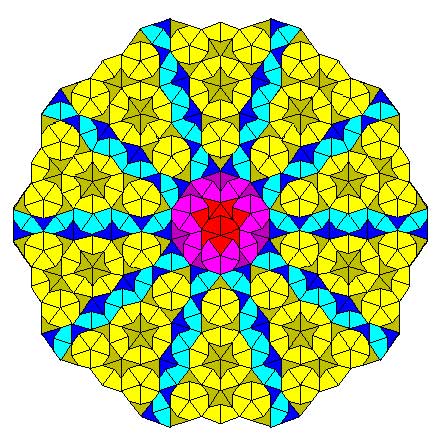
This einStein, called the ‘hat’ (some prefer ‘t-shirt’), has a very simple form : you take the most symmetric of all plane tessellations, $\ast 632$ in Conway’s notation, and glue sixteen copies of its orbifold (or if you so prefer, eight ‘kites’) to form the gray region below:

(all images copied from the aperiodic monotile paper)

Surprisingly, you do not even need to impose gluing conditions (unlike in the two-piece aperiodic kite and dart Penrose tilings), but you’ll need flipped hats to fill up the gaps left.

A few years ago, I wrote some posts on Penrose tilings, including details on inflation and deflation, aperiodicity, uncountability, Conway worms, and more:

To prove that hats tile the plane, and do so aperiodically, the authors do not apply inflation and deflation directly on the hats, but rather on associated tilings by ‘meta-tiles’ (rough outlines of blocks of hats). To understand these meta-tiles it is best to look at a large patch of hats:

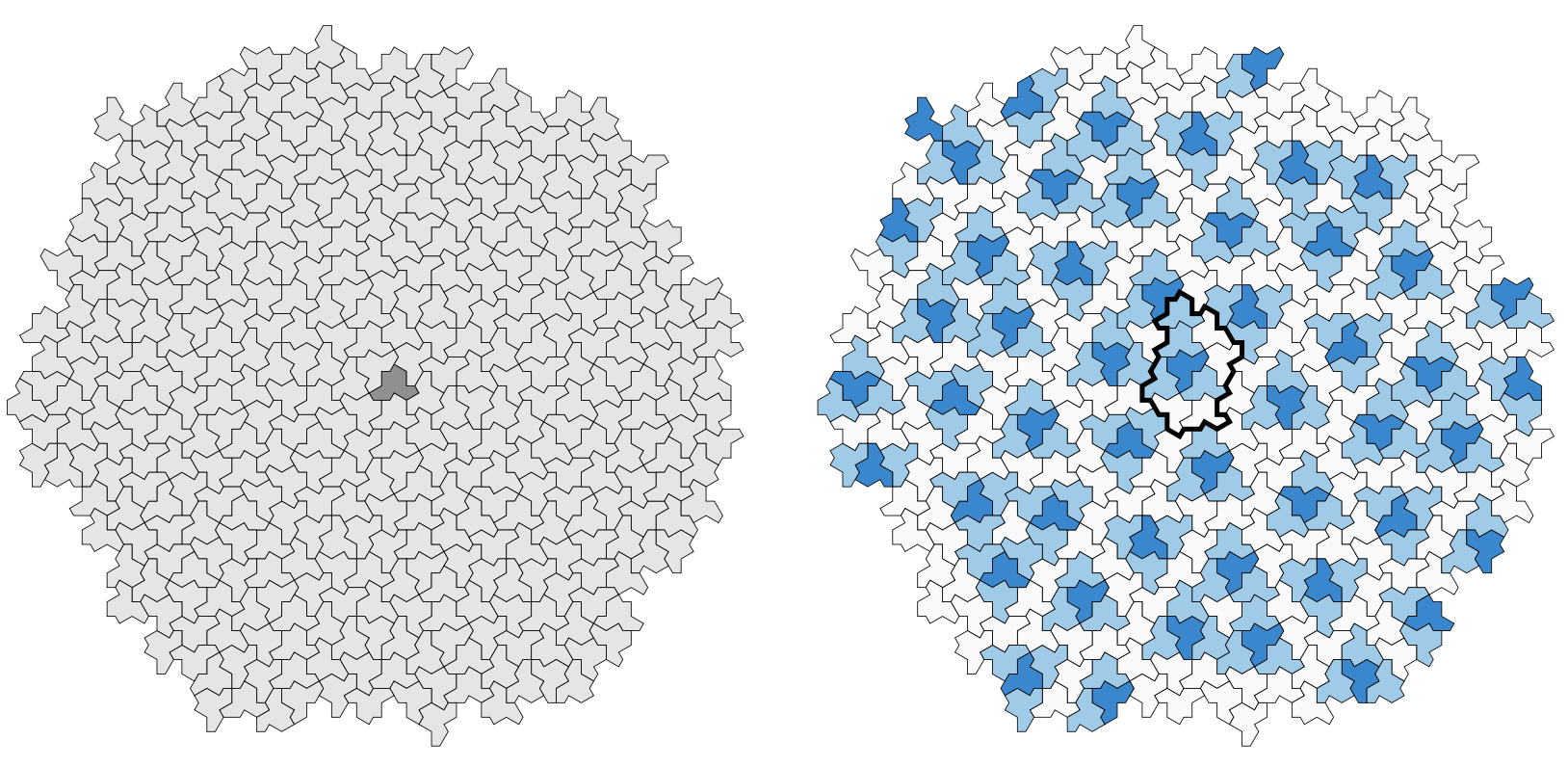
Here, the dark-blue hats are the ‘flipped’ ones, and the thickened outline around the central one gives the boundary of the ’empire’ of a flipped hat, that is, the collection of all forced tiles around it. So, around each flipped hat we find such an empire, possibly with different orientation. Also note that most of the white hats (there are also isolated white hats at the centers of triangles of dark-blue hats) make up ‘lines’ similar to the Conway worms in the case of the Penrose tilings. We can break up these ‘worms’ into ‘propeller-blades’ (gray) and ‘parallelograms’ (white). This gives us four types of blocks, the ‘meta-tiles’:

The empire of a flipped hat consists of an H-block (for Hexagon) made of one dark-blue (flipped) and three light-blue (ordinary) hats, one P-block (for Parallelogram), one F-block (for Fylfot, a propellor blade), and one T-block (for Triangle) for the remaining hat.

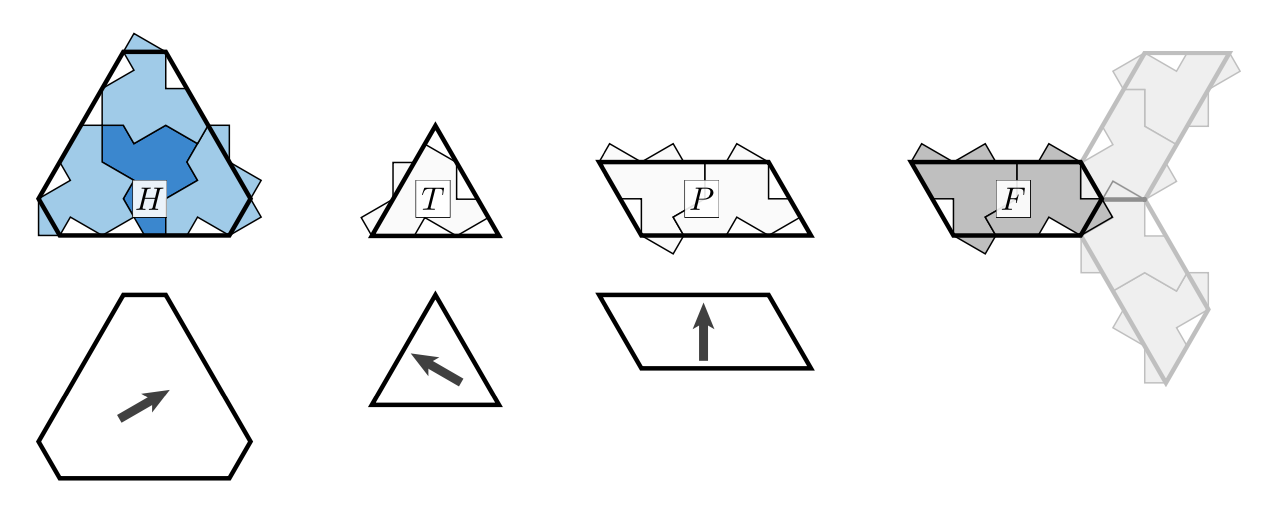
The H,T and P blocks have rotational symmetries, whereas the underlying block of hats does not. So we mark the intended orientation of the hats by an arrow, pointing to the side having two or three hat-pieces sticking out.

Any hat-tiling gives us a tiling with the meta-tile pieces H,T,P and F. Conversely, not every tiling by meta-tiles has an underlying hat-tiling, so we have to impose gluing conditions on the H,T,P and F-pieces. We can do this by using the boundary of the underlying hat-block, cutting away and adding hat-parts. Then, any H,T,P and F-tiling satisfying these gluing conditions will come from an underlying hat-tiling.

The idea is now to devise ‘inflation’- and ‘deflation’-rules for the H,T,P and F-pieces. For ‘inflation’ start from a tiling satisfying the gluing (and orientation) conditions, and look for the central points of the propellors (the thick red points in the middle picture).

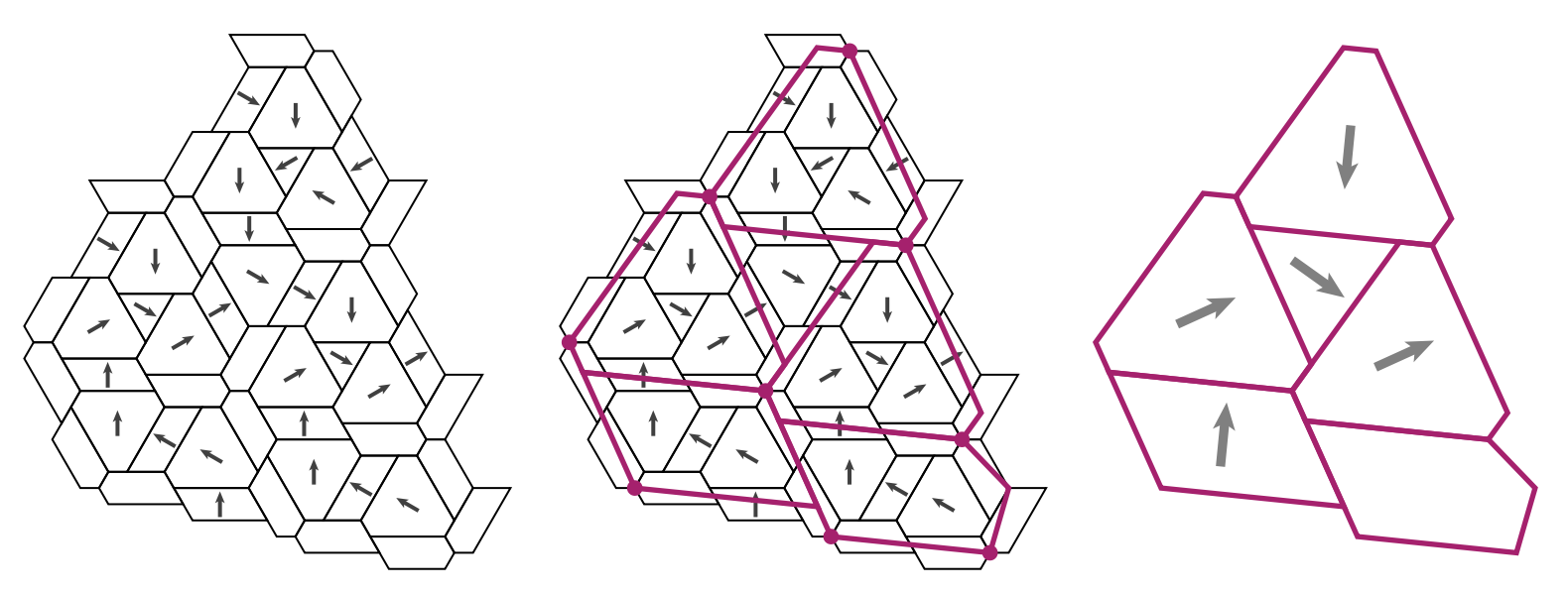
These points will determine the shape of the larger H,T,P and F-pieces, together with their orientations. The authors provide an applet to see these inflations in action.

Choose your meta-tile (H,T,P or F), then click on ‘Build Supertiles’ a number of times to get larger and larger tilings, and finally unmark the ‘Draw Supertiles’ button to get a hat-tiling.

For ‘deflation’ we can cut up H,T,P and F-pieces into smaller ones as in the pictures below:

Clearly, the hard part is to verify that these ‘inflated’ and ‘deflated’ tilings still satisfy the gluing conditions, so that they will have an underlying hat-tiling with larger (resp. smaller) hats.

This calls for a lengthy case-by-case analysis which is the core-part of the paper and depends on computer-verification.

Once this is verified, aperiodicity follows as in the case of Penrose tilings. Suppose a tiling is preserved under translation by a vector $\vec{v}$. As ‘inflation’ and ‘deflation’ only depend on the direct vicinity of a tile, translation by $\vec{v}$ is also a symmetry of the inflated tiling. Now, iterate this process until the diameter of the large tiles becomes larger than the length of $\vec{v}$ to obtain a contradiction.

Siobhan Roberts wrote a fine article Elusive ‘Einstein’ Solves a Longstanding Math Problem for the NY-times on this einStein.

It would be nice to try this strategy on other symmetric tilings: break the symmetry by gluing together a small number of its orbifolds in such a way that this extended tile (possibly with its reversed image) tile the plane, and find out whether you discovered a new einStein!

Leave a Comment

Penrose tilings are aperiodic tilings of the plane, made from 2 sort of tiles : kites and darts. It is well known (see for example the standard textbook tilings and patterns section 10.5) that one can describe a Penrose tiling around a given point in the plane as an infinite sequence of 0’s and 1’s, subject to the condition that no two consecutive 1’s appear in the sequence. Conversely, any such sequence is the sequence of a Penrose tiling together with a point. Moreover, if two such sequences are eventually the same (that is, they only differ in the first so many terms) then these sequences belong to two points in the same tiling,

Another remarkable feature of Penrose tilings is their local isomorphism : fix a finite region around a point in one tiling, then in any other Penrose tiling one can find a point having an isomorphic region around it. For this reason, the space of all Penrose tilings has horrible topological properties (all points lie in each others closure) and is therefore a prime test-example for the techniques of noncommutative geometry.

In his old testament, Noncommutative Geometry, Alain Connes associates to this space a $C^*$-algebra $Fib$ (because it is constructed from the Fibonacci series $F_0,F_1,F_2,…$) which is the direct limit of sums of two full matrix-algebras $S_n$, with connecting morphisms

$S_n = M_{F_n}(\mathbb{C}) \oplus M_{F_{n-1}}(\mathbb{C}) \rightarrow S_{n+1} = M_{F_{n+1}}(\mathbb{C}) \oplus M_{F_n}(\mathbb{C}) \qquad (a,b) \mapsto ( \begin{matrix} a & 0 \\ 0 & b \end{matrix}, a)$

As such $Fib$ is an AF-algebra (for approximately finite) and hence formally smooth. That is, $Fib$ would be the coordinate ring of a smooth variety in the noncommutative sense, if only $Fib$ were finitely generated. However, $Fib$ is far from finitely generated and has other undesirable properties (at least for a noncommutative algebraic geometer) such as being simple and hence in particular $Fib$ has no finite dimensional representations…

A couple of weeks ago, Paul Smith discovered a surprising connection between the noncommutative space of Penrose tilings and an affine algebra in the paper The space of Penrose tilings and the non-commutative curve with homogeneous coordinate ring $\mathbb{C} \langle x,y \rangle/(y^2)$.

Giving $x$ and $y$ degree 1, the algebra $P = \mathbb{C} \langle x,y \rangle/(y^2)$ is obviously graded and noncommutative projective algebraic geometers like to associate to such algebras their ‘proj’ which is the quotient category of the category of all graded modules in which two objects become isomorphisc iff their ‘tails’ (that is forgetting the first few homogeneous components) are isomorphic.

The first type of objects NAGers try to describe are the point modules, which correspond to graded modules in which every homogeneous component is 1-dimensional, that is, they are of the form

$\mathbb{C} e_0 \oplus \mathbb{C} e_1 \oplus \mathbb{C} e_2 \oplus \cdots \oplus \mathbb{C} e_n \oplus \mathbb{C} e_{n+1} \oplus \cdots$

with $e_i$ an element of degree $i$. The reason for this is that point-modules correspond to the points of the (usual, commutative) projective variety when the affine graded algebra is commutative.

Now, assume that a Penrose tiling has been given by a sequence of 0’s and 1’s, say $(z_0,z_1,z_2,\cdots)$, then it is easy to associate to it a graded vectorspace with action given by

$x.e_i = e_{i+1}$ and $y.e_i = z_i e_{i+1}$

Because the sequence has no two consecutive ones, it is clear that this defines a graded module for the algebra $P$ and determines a point module in $\pmb{proj}(P)$. By the equivalence relation on Penrose sequences and the tails-equivalence on graded modules it follows that two sequences define the same Penrose tiling if and only if they determine the same point module in $\pmb{proj}(P)$. Phrased differently, the noncommutative space of Penrose tilings embeds in $\pmb{proj}(P)$ as a subset of the point-modules for $P$.

The only such point-module invariant under the shift-functor is the one corresponding to the 0-sequence, that is, corresponds to the cartwheel tiling

Another nice consequence is that we can now explain the local isomorphism property of Penrose tilings geometrically as a consequence of the fact that the $Ext^1$ between any two such point-modules is non-zero, that is, these noncommutative points lie ‘infinitely close’ to each other.

This is the easy part of Paul’s paper.

The truly, truly amazing part is that he is able to recover Connes’ AF-algebra $Fib$ from $\pmb{proj}(P)$ as the algebra of global sections! More precisely, he proves that there is an equivalence of categories between $\pmb{proj}(P)$ and the category of all $Fib$-modules $\pmb{mod}(Fib)$!

In other words, the noncommutative projective scheme $\pmb{proj}(P)$ is actually isomorphic to an affine scheme and as its coordinate ring is formally smooth $\pmb{proj}(P)$ is a noncommutative smooth variety. It would be interesting to construct more such examples of interesting AF-algebras appearing as local rings of sections of proj-es of affine graded algebras.

2 Comments

Tag: Smith

an einStein

Penrose tilings and noncommutative geometry