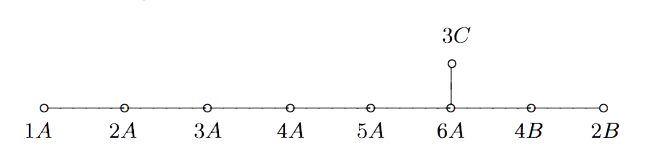
If you take two Fischer involutions in the monster (elements of conjugacy class 2A) and multiply them, the resulting element surprisingly belongs to one of just 9 conjugacy classes:
1A,2A,2B,3A,3C,4A,4B,5A or 6A
The orders of these elements are exactly the dimensions of the fundamental root for the extended $E_8$ Dynkin diagram.
This is the content of John McKay’s E(8)-observation : there should be a precise relation between the nodes of the extended Dynkin diagram and these 9 conjugacy classes in such a way that the order of the class corresponds to the component of the fundamental root. More precisely, one conjectures the following correspondence:
John Duncan found such a connection by considering carefully the corresponding moonshine groups and their inter-relation. For more on this, look at the old post E8 from moonshine groups. The extended Dynkin diagram with these moonshine groups as vertices is:
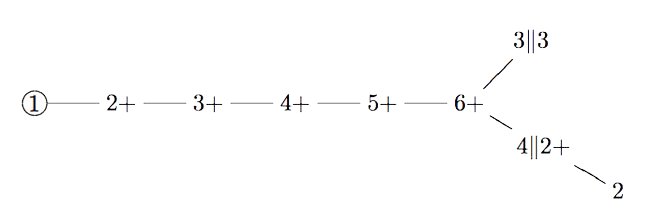
Duncan does this by assigning numbers to moonshine groups: the dimension is the order of the corresponding monster element and the valency is one more than the copies of $C_2$ generated by the Atkin-Lehner involutions in the moonshine group.
One might ask whether there is a graph on all 171 moonshine groups, compatible with the valencies of every vertex.
Now, even for the 9 groups in McKay’s question, the valencies do not determine the graph uniquely and Duncan proceeds with an ad hoc condition on the edges.
There is a partition on the 9 groups by the property whether or not the index of the intersection with $\Gamma_0(2)$ is at most two. Then Duncan declares that there cannot be an edge between two groups belonging to the same class.
His motivation for this property comes from classical McKay-correspondence for the binary icosahedral group (where the vertices correspond to simple representations $S$, and the edges from $S$ to factors of $S \otimes V_2$, where $V_2$ is the restriction of the standard $2$-dimensional simple for $SU(2)$).
Of the $9$ simples there are only $4$ faithful ones, $5$ come from simples of $A_5$. Because $\Gamma_0(2)$ is a subgroup of the modular group of index 2, he then views $\Gamma_0(2)$ as similar to the subgroup $A_5$ in the binary icosahedral group, and declares a moonshine group to be faithful if its index in the intersection with $\Gamma_0(2)$ is at most two.
One might ask whether there is another, more natural, definition for having an edge (or multiple ones) between arbitrary moonshine groups.
And, what is the full graph on the 171 groups?
Leave a Comment