Are the valencies of the 171 moonshine groups are compatible, that is, can one construct a (disconnected) graph on the 171 vertices such that in every vertex (determined by a moonshine group G) the vertex-valency coincides with the valency of the corresponding group? Duncan describes a subset of 9 moonshine groups for which the valencies are compatible. These 9 groups are characterized as those moonshine groups G
having width 1 at the cusp and such that their intersection with the modular group is big.
 Time to wrap up this series on John Duncan‘s paper Arithmetic groups and the affine E8 Dynkin diagram in which he gives a realization of the extended E(8)-Dynkin diagram (together with its isotropic root vector) from the moonshine groups, compatible with McKay’s E(8)-observation.
Time to wrap up this series on John Duncan‘s paper Arithmetic groups and the affine E8 Dynkin diagram in which he gives a realization of the extended E(8)-Dynkin diagram (together with its isotropic root vector) from the moonshine groups, compatible with McKay’s E(8)-observation.
In the previous post we have described all 171 moonshine groups using Conway’s big picture. This description will allow us to associate two numbers to a moonshine group $G \subset PSL_2(\mathbb{R}) $.
Recall that for any such group we have a positive integer $N $ such that
$\Gamma_0(N) \subset G \subset \Gamma_0(h,\frac{N}{h})+ $
where $h $ is the largest divisor of 24 such that $h^2 | N $. Let us call $n_G=\frac{N}{h} $ the dimension of $G $ (Duncan calls this number the ‘normalized level’) as it will give us the dimension component at the vertex determined by $G $.
We have also seen last time that any moonshine group is of the form $G = \Gamma_0(n_G || h)+e,f,g $, that is, $G/\Gamma_0(n_G ||h) $ is an elementary abelian group $~(\mathbb{Z}/2\mathbb{Z})^m $ generated by Atkin-Lehner involutions. Let’s call $v_G=m+1 $ the valency of the group $G $ as it will give s the valency of the vertex determined by $G $.
It would be nice to know whether the valencies of the 171 moonshine groups are compatible, that is, whether one can construct a (disconnected) graph on the 171 vertices such that in each vertex (determined by a moonshine group $G $) the vertex-valency coincides with the valency of the corresponding group.
Duncan describes a subset of 9 moonshine groups for which the valencies are compatible. These 9 groups are characterized as those moonshine groups $G $
having width 1 at the cusp and such that their intersection with the modular group $\Gamma = PSL_2(\mathbb{Z}) $ is big, more precisely the index $[\Gamma : \Gamma \cap G] \leq 12 $ and $[\Gamma : \Gamma \cap G]/[G : \Gamma \cap G] \leq 3 $.
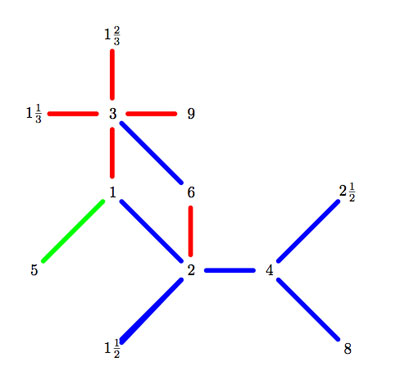 They can be described using the mini-moonshine picture on the right. They are :
They can be described using the mini-moonshine picture on the right. They are :
The modular group itself $1=\Gamma $, being the stabilizer of the lattice 1. This group has clearly dimension and valency equal to one.
The modular subgroup $2=\Gamma_0(2) $ being the point-wise stabilizer of the lattices 1 and 2 (so it has valency one and dimension two, and, its normalizer $2+ =\Gamma_0(2)+ $ which is the set-wise stabilizer of the lattices 1 and 2 and the one Atkin-Lehner involution interchanges both. So, this group has valency two (as we added one involution) as well as dimension two.
Likewise, the groups $3+=\Gamma_0(3)+ $ and $5+=\Gamma_0(5)+ $ are the stabilzer subgroups of the red 1-cell (1,3) resp. the green 1-cell (1,5) and hence have valency two (as we add one involution) and dimensions 3 resp. 5.
The group $4+=\Gamma_0(4)+ $ stabilizes the (1|4)-thread and as we add one involution must have valency 2 and dimension 4.
On the other hand, the group $6+=\Gamma_0(6)+ $ stabilizes the unique 2-cell in the picture (having lattices 1,2,3,6) so this time we will add three involutions (horizontal and vertical switches and their product the antipodal involution). Hence, for this group the valency is three and its dimension is equal to six.
Remain the two groups connected to the mini-snakes in the picture. The red mini-snake (top left hand) is the ball with center 3 and hyperdistance 3 and determines the group $3||3=\Gamma_0(3||3) $ which has valency one (we add no involutions) and dimension 3. The blue mini-snake (the extended D(5)-Dynkin in the lower right corner) determines the group $4||2+=\Gamma(4||2)+ $ which has valency two and dimension 4.
The valencies of these 9 moonshine groups are compatible and they can be arranged in the extended E(8) diagram depicted below
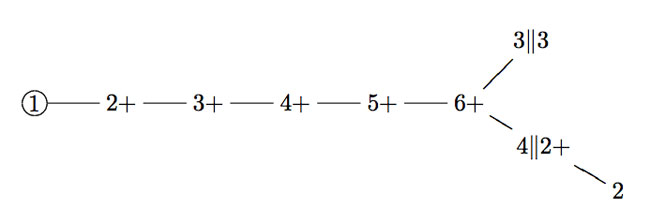
Moreover, the dimensions of the groups give the exact dimension-components of the isotropic root of the extended E(8)-diagram. Further, the dimension of the group is equal to the order of the elements making up the conjugacy class of the monster to which exactly the given groups correspond via monstrous moonshine and hence compatible with John McKay‘s original E(8)-observation!
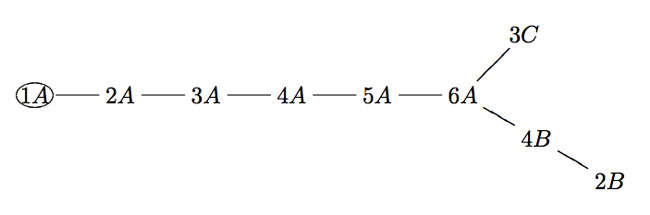
Once again, I would love to hear when someone has more information on the cell-decomposition of the moonshine picture or if someone can extend the moonshine E(8)-graph, possibly to include all 171 moonshine groups.
One Comment