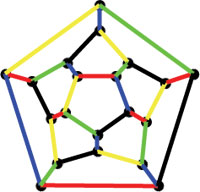
A _quintomino_ is a regular pentagon having all its sides
colored by five different colours. Two quintominoes are the same if they
can be transformed into each other by a symmetry of the pentagon (that
is, a cyclic rotation or a flip of the two faces). It is easy to see
that there are exactly 12 different quintominoes. On the other hand,
there are also exactly 12 pentagonal faces of a dodecahedron
whence the puzzling question whether the 12 quintominoes can be joined
together (colours mathching) into a dodecahedron.
According to
the Dictionnaire de
mathematiques recreatives this can be done and John Conway found 3
basic solutions in 1959. These 3 solutions can be found from the
diagrams below, taken from page 921 of the reprinted Winning Ways for your Mathematical
Plays (volume 4) where they are called _the_ three
quintominal dodecahedra giving the impression that there are just 3
solutions to the puzzle (up to symmetries of the dodecahedron). Here are
the 3 Conway solutions
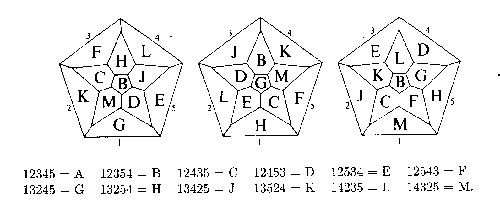
One projects the dodecahedron down from the top face which is
supposed to be the quintomino where the five colours red (1), blue (2),
yellow (3), green (4) and black(5) are ordered to form the quintomino of
type A=12345. Using the other quintomino-codes it is then easy to work
out how the quintominoes fit together to form a coloured dodecahedron.
In preparing to explain this puzzle for my geometry-101 course I
spend a couple of hours working out a possible method to prove that
these are indeed the only three solutions. The method is simple : take
one or two of the bottom pentagons and fill then with mathching
quintominoes, then these more or less fix all the other sides and
usually one quickly runs into a contradiction.
However, along the
way I found one case (see top picture) which seems to be a _new_
quintominal dodecahedron. It can't be one of the three Conway-types
as the central quintomino is of type F. Possibly I did something wrong
(but what?) or there are just more solutions and Conway stopped after
finding the first three of them…
Update (with help from
Michel Van den Bergh) Here is an elegant way to construct
'new' solutions from existing ones, take a permutation $\\sigma
\\in S_5$ permuting the five colours and look on the resulting colored
dodecahedron (which again is a solution) for the (new) face of type A
and project from it to get a new diagram. Probably the correct statement
of the quintominal-dodecahedron-problem is : find all solutions up to
symmetries of the dodecahedron _and_ permutations of the colours.
Likely, the 3 Conway solutions represent the different orbits under this
larger group action. Remains the problem : to which orbit belongs the
top picture??
Comments