A natural question these days might be: “what are the rotational symmetries of the Covid-19 virus?”
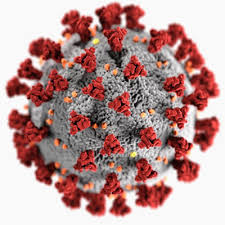
Most illustrations show a highly symmetric object, suggesting it might have icosahedral symmetry. In fact, many viruses do have icosahedral symmetry as a result of the ‘genetic economy principle’ proposed by Watson and Crick in 1956, resulting in the Caspar-Klug classification of viral capsids.
But then, perhaps this icosahedral illusion is a result of design decisions illustrators made turning scientific data into pictures. Veronica Falconieri Hays wrote a beautiful article describing the effort going into this: How I built a 3d-model of the coronavirus for Scientific American. Here’s her final picture
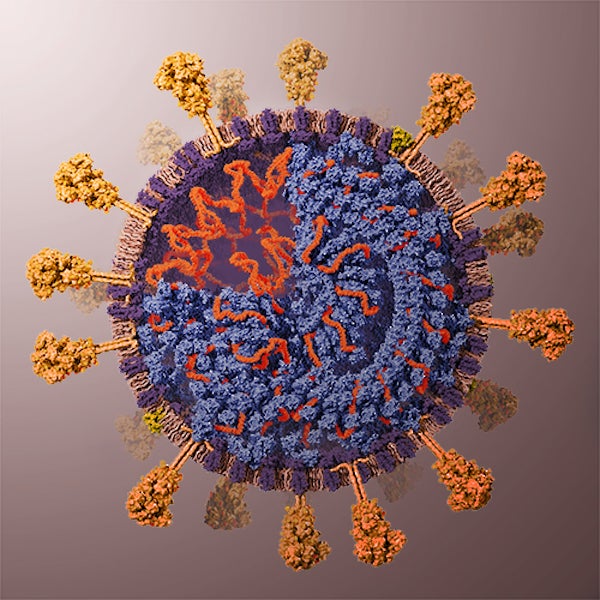
And yes, icosahedral symmetry was one of her design decisions:
The M proteins form pairs, and it is estimated that there are 16–25 M proteins per spike on the surface of the virus. I ended up modeling 10 M protein pairs (so 20 M proteins) per spike in my model. Some researchers hypothesize that the M proteins form a lattice within the envelope (interacting with an underlying lattice of N proteins; see below). I decided to use an icosahedral sphere to create a regular distribution of the M protein dimers to hint at this hypothesis.
The spikes (or S-proteins) are the tentacles in these pictures, and one of the few hard figures on Corona is that ‘on average’ there are 74 of them.
This fact is enough to rule out icosahedral symmetry.
If the icosahedral rotation group (of order $60$, isomorphic to $A_5$) acts on the $74$ spikes, then each orbit consists of $60$ spikes unless that spike lies on a twofold, threefold or fivefold rotation axis, in which cases the number of spikes in its orbit are respectively $30$, $20$ or $12$. So, we can’t get a total number of $74$ spikes!
However, just looking at the number of spikes we cannot rule out octahedral symmetry!
The octahedral rotation group (of order $24$, isomorphic to $S_4$) will have orbits of size $24$ unless the spike lies on a twofold, threefold or fourfold rotation axis, giving orbits of size $12$, $8$ and $6$ respectively (the midpoints of edges, the vertices and the midpoints of faces of the octahedron), and
\[
74 = 24+24+12+8+6 \]
The most symmetric arrangement of spikes would be to subdivide each of the $8$ triangular faces of the octahedron into $6$ triangles with vertices the midpoint of the face, a vertex and a midpoint of an edge, and then to position the spikes on the axis through the vertices and midpoints of these smaller triangles.
Googling around I found very few references to symmetries of Covid-19, probably because it has an helical RNA-coil, which seems not to go well with Caspar-Klug type polyhedral viral capsids.
Here’s an exception: A structural model for the Coronavirus nucleocapsid by Federico Coscio, Alejandro D. Nadra, and Diego U. Ferreiro.
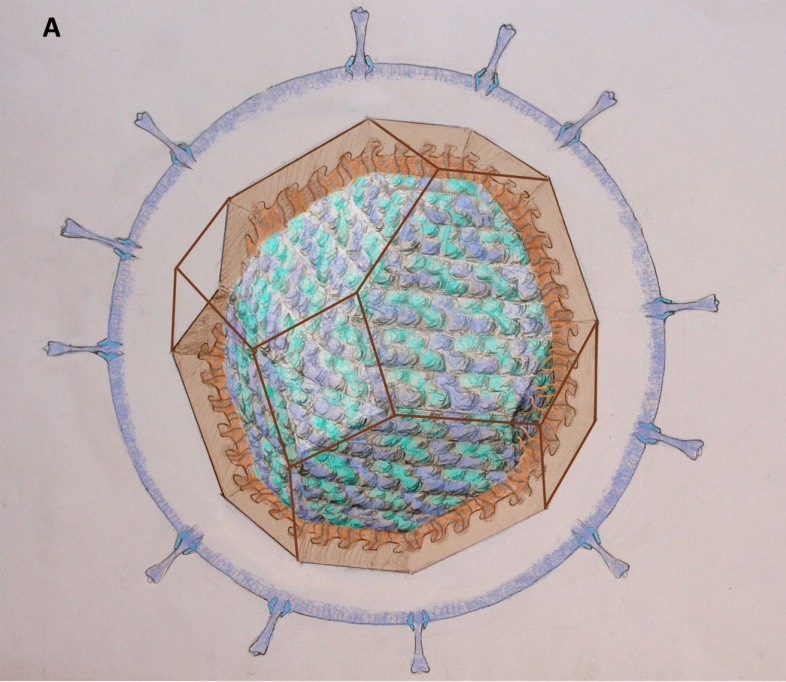
They propose a truncated octahedron as capsid (in transparent brown) with interior a continuous coil packing of blue and cyan helices. The virus membrane with the spikes and M proteins is drawn in blue.
If you have better info or references on the (conjectural) symmetries of Covid-19, please leave a comment.
One Comment