A long while ago I promised to take you from the action by the modular group $\Gamma=PSL_2(\mathbb{Z})$ on the lattices at hyperdistance $n$ from the standard orthogonal laatice $L_1$ to the corresponding ‘monstrous’ Grothendieck dessin d’enfant.
Speaking of dessins d’enfant, let me point you to the latest intriguing paper by Yuri I. Manin and Matilde Marcolli, ArXived a few days ago Quantum Statistical Mechanics of the Absolute Galois Group, on how to build a quantum system for the absolute Galois group from dessins d’enfant (more on this, I promise, later).
Where were we?
We’ve seen natural one-to-one correspondences between (a) points on the projective line over $\mathbb{Z}/n\mathbb{Z}$, (b) lattices at hyperdistance $n$ from $L_1$, and (c) coset classes of the congruence subgroup $\Gamma_0(n)$ in $\Gamma$.
How to get from there to a dessin d’enfant?
The short answer is: it’s all in Ravi S. Kulkarni’s paper, “An arithmetic-geometric method in the study of the subgroups of the modular group”, Amer. J. Math 113 (1991) 1053-1135.
It is a complete mystery to me why Tatitscheff, He and McKay don’t mention Kulkarni’s paper in “Cusps, congruence groups and monstrous dessins”. Because all they do (and much more) is in Kulkarni.
I’ve blogged about Kulkarni’s paper years ago:
– In the Dedekind tessalation it was all about assigning special polygons to subgroups of finite index of $\Gamma$.
– In Modular quilts and cuboid tree diagram it did go on assigning (multiple) cuboid trees to a (conjugacy class) of such finite index subgroup.
– In Hyperbolic Mathieu polygons the story continued on a finite-to-one connection between special hyperbolic polygons and cuboid trees.
– In Farey codes it was shown how to encode such polygons by a Farey-sequence.
– In Generators of modular subgroups it was shown how to get generators of the finite index subgroups from this Farey sequence.
The modular group is a free product
\[
\Gamma = C_2 \ast C_3 = \langle s,u~|~s^2=1=u^3 \rangle \]
with lifts of $s$ and $u$ to $SL_2(\mathbb{Z})$ given by the matrices
\[
S=\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix},~\qquad U= \begin{bmatrix} 0 & -1 \\ 1 & -1 \end{bmatrix} \]
As a result, any permutation representation of $\Gamma$ on a set $E$ can be represented by a $2$-coloured graph (with black and white vertices) and edges corresponding to the elements of the set $E$.
Each white vertex has two (or one) edges connected to it and every black vertex has three (or one). These edges are the elements of $E$ permuted by $s$ (for white vertices) and $u$ (for black ones), the order of the 3-cycle determined by going counterclockwise round the vertex.
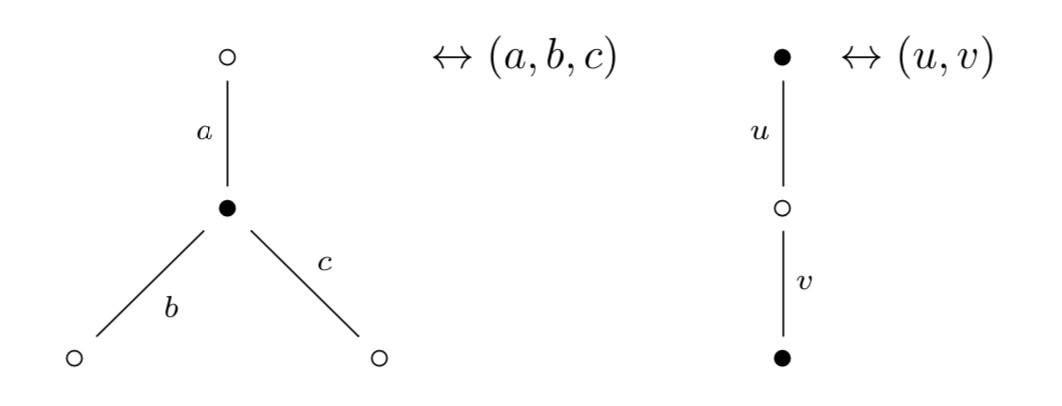
Clearly, if there’s just one edge connected to a vertex, it gives a fixed point (or 1-cycle) in the corresponding permutation.
The ‘monstrous dessin’ for the congruence subgroup $\Gamma_0(n)$ is the picture one gets from the permutation $\Gamma$-action on the points of $\mathbb{P}^1(\mathbb{Z}/n \mathbb{Z})$, or equivalently, on the coset classes or on the lattices at hyperdistance $n$.
Kulkarni’s paper (or the blogposts above) tell you how to get at this picture starting from a fundamental domain of $\Gamma_0(n)$ acting on teh upper half-plane by Moebius transformations.
Sage gives a nice image of this fundamental domain via the command
FareySymbol(Gamma0(n)).fundamental_domain()
Here’s the image for $n=6$:
.jpg)
The boundary points (on the halflines through $0$ and $1$ and the $4$ half-circles need to be identified which is indicaed by matching colours. So the 2 halflines are identified as are the two blue (and green) half-circles (in opposite direction).
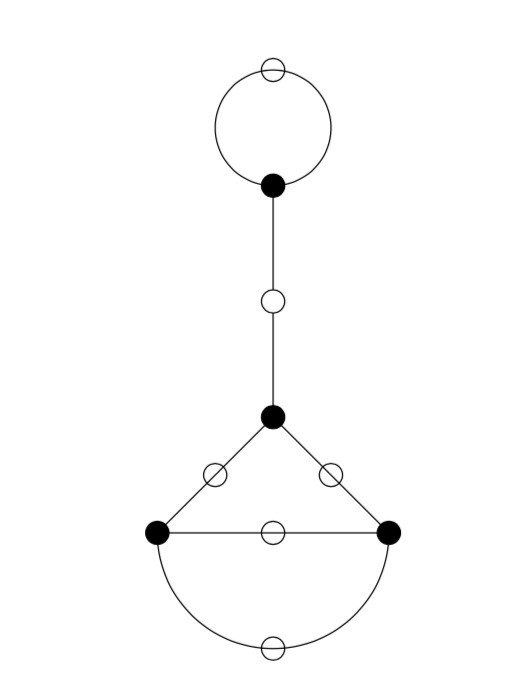
To get the dessin from this, let’s first look at the interior points. A white vertex is a point in the interior where two black and two white tiles meet, a black vertex corresponds to an interior points where three black and three white tiles meet.
Points on the boundary where tiles meet are coloured red, and after identification two of these reds give one white or black vertex. Here’s the intermediate picture

The two top red points are identified giving a white vertex as do the two reds on the blue half-circles and the two reds on the green half-circles, because after identification two black and two white tiles meet there.
This then gives us the ‘monstrous’ modular dessin for $n=6$ of the Tatitscheff, He and McKay paper:
Let’s try a more difficult example: $n=12$. Sage gives us as fundamental domain

giving us the intermediate picture

and spotting the correct identifications, this gives us the ‘monstrous’ dessin for $\Gamma_0(12)$ from the THM-paper:
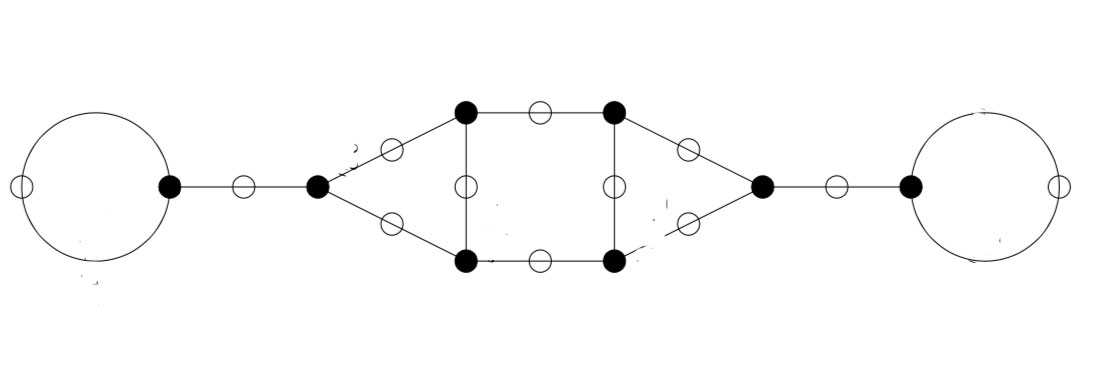
In general there are several of these 2-coloured graphs giving the same permutation representation, so the obtained ‘monstrous dessin’ depends on the choice of fundamental domain.
You’ll have noticed that the domain for $\Gamma_0(6)$ was symmetric, whereas the one Sage provides for $\Gamma_0(12)$ is not.
This is caused by Sage using the Farey-code
\[
\xymatrix{
0 \ar@{-}[r]_1 & \frac{1}{6} \ar@{-}[r]_1 & \frac{1}{5} \ar@{-}[r]_2 & \frac{1}{4} \ar@{-}[r]_3 & \frac{1}{3} \ar@{-}[r]_4 & \frac{1}{2} \ar@{-}[r]_4 & \frac{2}{3} \ar@{-}[r]_3 & \frac{3}{4} \ar@{-}[r]_2 & 1}
\]
One of the nice results from Kulkarni’s paper is that for any $n$ there is a symmetric Farey-code, giving a perfectly symmetric fundamental domain for $\Gamma_0(n)$. For $n=12$ this symmetric code is
\[
\xymatrix{
0 \ar@{-}[r]_1 & \frac{1}{6} \ar@{-}[r]_2 & \frac{1}{4} \ar@{-}[r]_3 & \frac{1}{3} \ar@{-}[r]_4 & \frac{1}{2} \ar@{-}[r]_4 & \frac{2}{3} \ar@{-}[r]_3 & \frac{3}{4} \ar@{-}[r]_2 & \frac{5}{6} \ar@{-}[r]_1 & 1}
\]
It would be nice to see whether using these symmetric Farey-codes gives other ‘monstrous dessins’ than in the THM-paper.
Remains to identify the edges in the dessin with the lattices at hyperdistance $n$ from $L_1$.
Using the tricks from the previous post it is quite easy to check that for any $n$ the monstrous dessin for $\Gamma_0(n)$ starts off with the lattices $L_{M,\frac{g}{h}} = M,\frac{g}{h}$ as below

Let’s do a sample computation showing that the action of $s$ on $L_n$ gives $L_{\frac{1}{n}}$:
\[
L_n.s = \begin{bmatrix} n & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} = \begin{bmatrix} 0 & -n \\ 1 & 0 \end{bmatrix} \]
and then, as last time, to determine the class of the lattice spanned by the rows of this matrix we have to compute
\[
\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} 0 & -n \\ 1 & 0 \end{bmatrix} = \begin{bmatrix} -1 & 0 \\ 0 & -n \end{bmatrix} \]
which is class $L_{\frac{1}{n}}$. And similarly for the other edges.
Do you intend to mean that Kulkarni’s paper and its methods could also have any implication for Manin & Marcolli arxiv preprint, you mentioned in the very start of your post?
@Devendra : Kulkarni tells you everything you need to know about modular dessins (that is, permutation representations of the modular group). Manin&Marcolli aim for all dessins (permutation reps of the free group on two generators or of $C_{\infty} \ast C_2$ for ‘clean’ dessins). At the moment there’s too much confusion on what M&M really want/need that we’d probably have to await a better version of their paper.