In the Learners and Poly-post we’ve seen that learners from $A$ to $B$ correspond to set-valued representations of a directed graph $G$ and therefore form a presheaf topos.
Any topos comes with its Mitchell-Benabou language, allowing us to speak of formulas, propositions and their truth values. Two objects play a special role in this: the terminal object $\mathbf{1}$, and the subobject classifier $\mathbf{\Omega}$. It is a fun exercise to determine these special learners.
$T$ is the free rooted tree with branches sprouting from every node $n \in T_0$ for each element in $A \times B$. $C$ will be our set of colours, one for each element of $Maps(A,B) \times Maps(A \times B,A)$.
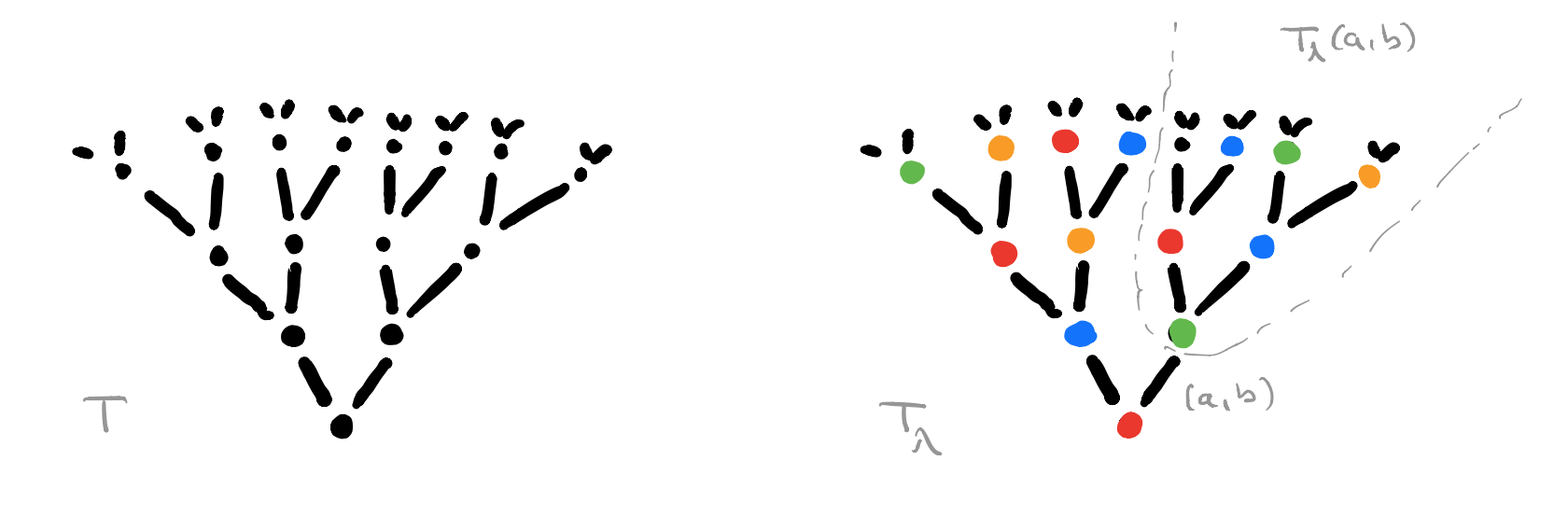
For every map $\lambda : T_0 \rightarrow C$ we get a coloured rooted tree $T_{\lambda}$, and for each branch $(a,b)$ from the root we get another rooted sub-tree $T_{\lambda}(a,b)$ which is again of the form $T_{\mu}$ for a certain map $\mu : T_0 \rightarrow C$.
The directed graph $G$ has a vertex $v_{\lambda} \in V$ for each coloured rooted tree $T_{\lambda}$ and a directed edge $v_{\lambda} \rightarrow v_{\mu}$ if $T_{\mu}$ is the isomorphism class of coloured rooted trees of the subtree $T_{\lambda}(a,b)$ for some $(a,b) \in A \times B$.
There are exactly $\# A \times B$ directed edges leaving every vertex in $G$, but there may be (many) more incoming edges. We can colour each vertex $v_{\lambda}$ with the colour of the root of $T_{\lambda}$.

The coloured directed graph $G$ depicts the learning process in a neural network, being trained to find a suitable map $A \rightarrow B$. The colour of a vertex $v_{\lambda}$ gives a map $f \in Maps(A,B)$ (and a request function). If the network now gives as output $b \in B$ for a given input $a \in A$, we can move on to the end-vertex $v_{\mu}$ of the directed edge labeled $(a,b)$ out of $v_{\lambda}$. The colour of $v_{\mu}$ gives us a new (hopefully improved) map $f_{new} \in Maps(A,B)$ (and a new request function). A new training data $(a’,b’)$ brings us to a new vertex and map, and so on.
Clearly, some parts of $G$ are more efficient to find the desired map than others, and the aim of the game is to distinguish efficient from inefficient learners. A first hint that Grothendieck topologies and their corresponding sheafifications will turn out to be important.
We’ve seen that a learner, that is a morphism $Py^P \rightarrow C y^{A \times B}$ in $\mathbf{Poly}$, assigns a set $P_{\lambda}$ to every vertex $v_{\lambda}$ (this set may be empty) and a map $P_{\lambda} \rightarrow P_{\mu}$ to every directed edge $v_{\lambda} \rightarrow v_{\mu}$ in $G$.
The terminal object $\mathbf{1}$ in this setting assigns to each vertex a singleton $\{ \ast \}$, and the obvious maps for each directed edge. In $\mathbf{Poly}$-speak, the terminal object is the morphism
\[
\mathbf{1}~:~V y^V \rightarrow C y^{A \times B} \]
which sends each vertex $v_{\lambda} \in V$ to its colour $c \in C$, and where the backtrack map $\varphi^{\#}_{v_{\lambda}}[c]$ maps $(a,b)$ to $v_{\mu}$ if this is the end-vertex of the edge labelled $(a,b)$ out of $v_{\lambda}$. That is, $\mathbf{1}$ contains all information about the coloured directed graph $G$.
The subobject classifier $\mathbf{\Omega}$ assigns to each vertex $v_{\lambda}$ the set $\mathbf{\Omega}(v_{\lambda})$ of all subsets $S$ of directed paths in $G$, starting at $v_{\lambda}$, such that if $p \in S$ then also all prolongated paths belong to $S$. Note that the emptyset $\emptyset$ satisfies this requirement, so is an element of this vertex set. Another special element in $\mathbf{\Omega}(v_{\lambda})$ is the set $\mathbf{1}_{\lambda}$ of all oriented paths starting at $v_{\lambda}$.
$\mathbf{\Omega}(v_{\lambda})$ is an Heyting algebra with $1=\mathbf{1}_{\lambda}$, $0 = \emptyset$, partially ordered via inclusion, and logical operations $\wedge$ (intersection), $\vee$ (union), $\neg$ (with $\neg S$ the largest $S’ \in \mathbf{\Omega}(v_{\lambda})$ disjoint from $S$) and $\Rightarrow$ defined by $S \Rightarrow S’$ is the union of all $S” \in \mathbf{\Omega}(v_{\lambda})$ such that $S” \cap S \subseteq S’$.

$S \wedge \neg S$ is not always equal to $1$. Here, the union misses the left edge from the root. So, we will not be able to prove things by contradiction.
If $v_{\lambda} \rightarrow v_{\mu}$ is the directed edge labeled $(a,b)$, then the corresponding map $\mathbf{\Omega}(v_{\lambda}) \rightarrow \mathbf{\Omega}(v_{\mu})$ takes an $S \in \mathbf{\Omega}(v_{\lambda})$, drops all paths which do not pass through $v_{\mu}$ and removes from those who do the initial edge $(a,b)$. If no paths in $S$ pass through $v_{\mu}$ then $S$ is mapped to $\emptyset \in \mathbf{\Omega}(v_{\mu})$.
If $\Omega = \bigsqcup_{\lambda} \mathbf{\Omega}(v_{\lambda})$ then the subobject classifier is the morphism in $\mathbf{Poly}$
\[
\mathbf{\Omega}~:~\Omega y^{\Omega} \rightarrow C y^{A \times B} \]
sending a path starting in $v_{\lambda}$ to the colour of $v_{\lambda}$ and the backtrack map of $(a,b)$ the image of the path under the map $\mathbf{\Omega}(v_{\lambda}) \rightarrow \mathbf{\Omega}(v_{\mu})$.
Ok, let’s define the Learner’s Mitchell-Benabou language.
We’ll view a learner $Py^P \rightarrow C y^{A \times B}$ as a set-valued representation $P$ of the directed graph $G$ with vertex set $P_{\lambda}$ placed at vertex $v_{\lambda}$.
A formula $\phi(p)$ of the language with a free variable $p$ is a morphism (of representations of $G$) from a learner $P$ to the subobject classifier
\[
\phi~:~P \rightarrow \mathbf{\Omega} \]
Such a morphism determines a sub-representation of $P$ which we can denote $\{ p | \phi(p) \}$ with vertex sets
\[
\{ p | \phi(p) \}_{\lambda} = \{ p \in P_{\lambda}~|~\phi(v_{\lambda})(p) = \mathbf{1}_{\lambda} \} \]
On formulas we can apply logical connectives to get more formulas. For example, the formula $\phi(p) \Rightarrow \psi(q)$ is the composition
\[
P \times Q \rightarrow^{\phi \times \psi} \mathbf{\Omega} \times \mathbf{\Omega} \rightarrow^{\Rightarrow} \mathbf{\Omega} \]
By quantifying all free variables we get a formula without free variables, and those correspond to morphisms $\mathbf{1} \rightarrow \mathbf{\Omega}$, that is, to sub-representations of the terminal object $\mathbf{1}$.
For example, if $\phi(p)$ is the formula with free variable $p$ corresponding to the morphism $\phi : P \rightarrow \mathbf{\Omega}$, then we have
\[
\forall p : \phi(p) = \{ v_{\lambda} \in V~|~\{ p | \phi(p) \}_{\lambda} = P_{\lambda} \} \]
and
\[
\exists p : \phi (p) = \{ v_{\lambda} \in V~|~\{ p | \phi(p) \}_{\lambda} \not= \emptyset \} \]
Sub-representations of $\mathbf{1}$ again form a Heyting-algebra in the obvious way, so we can assign a “truth-value” to a formula without free variables as that sub-object of $\mathbf{1}$.
There’s a lot more to say, so perhaps this will be continued.
Comments