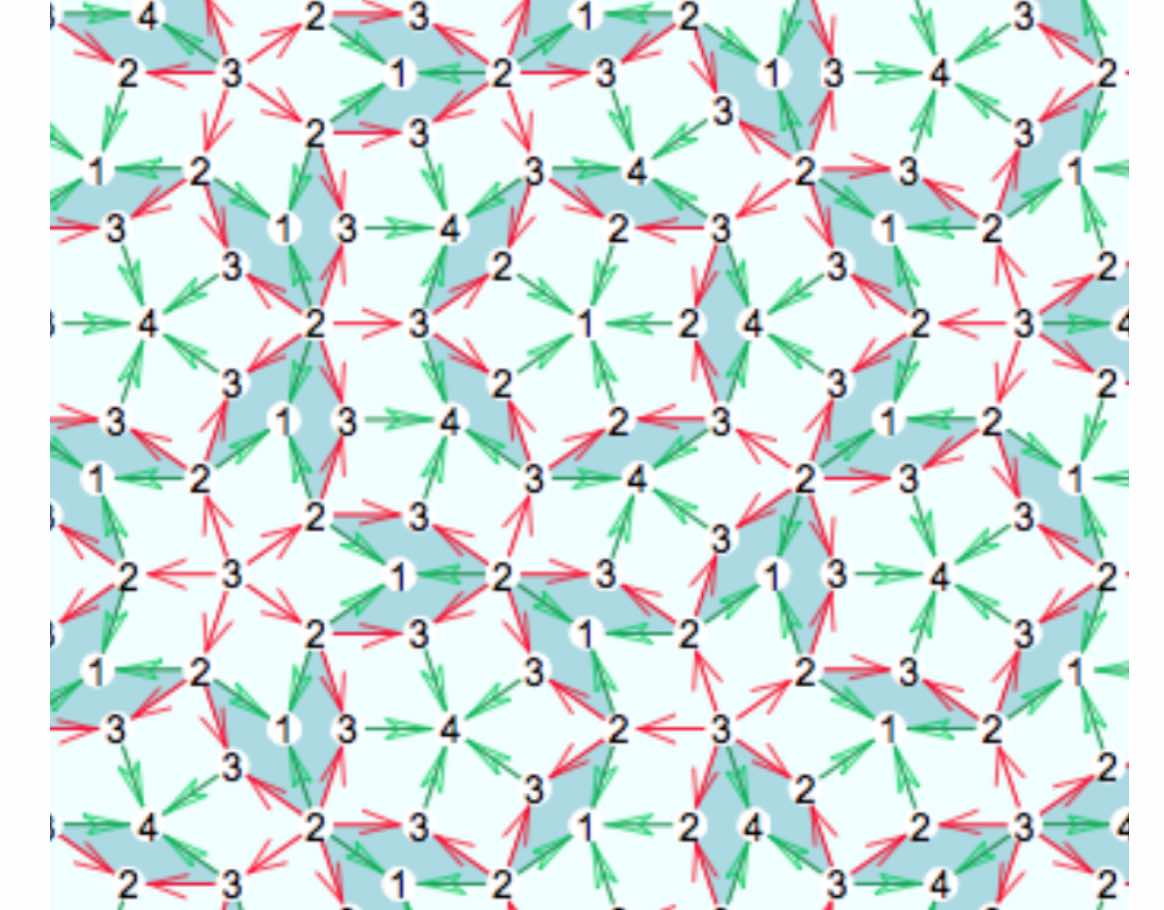
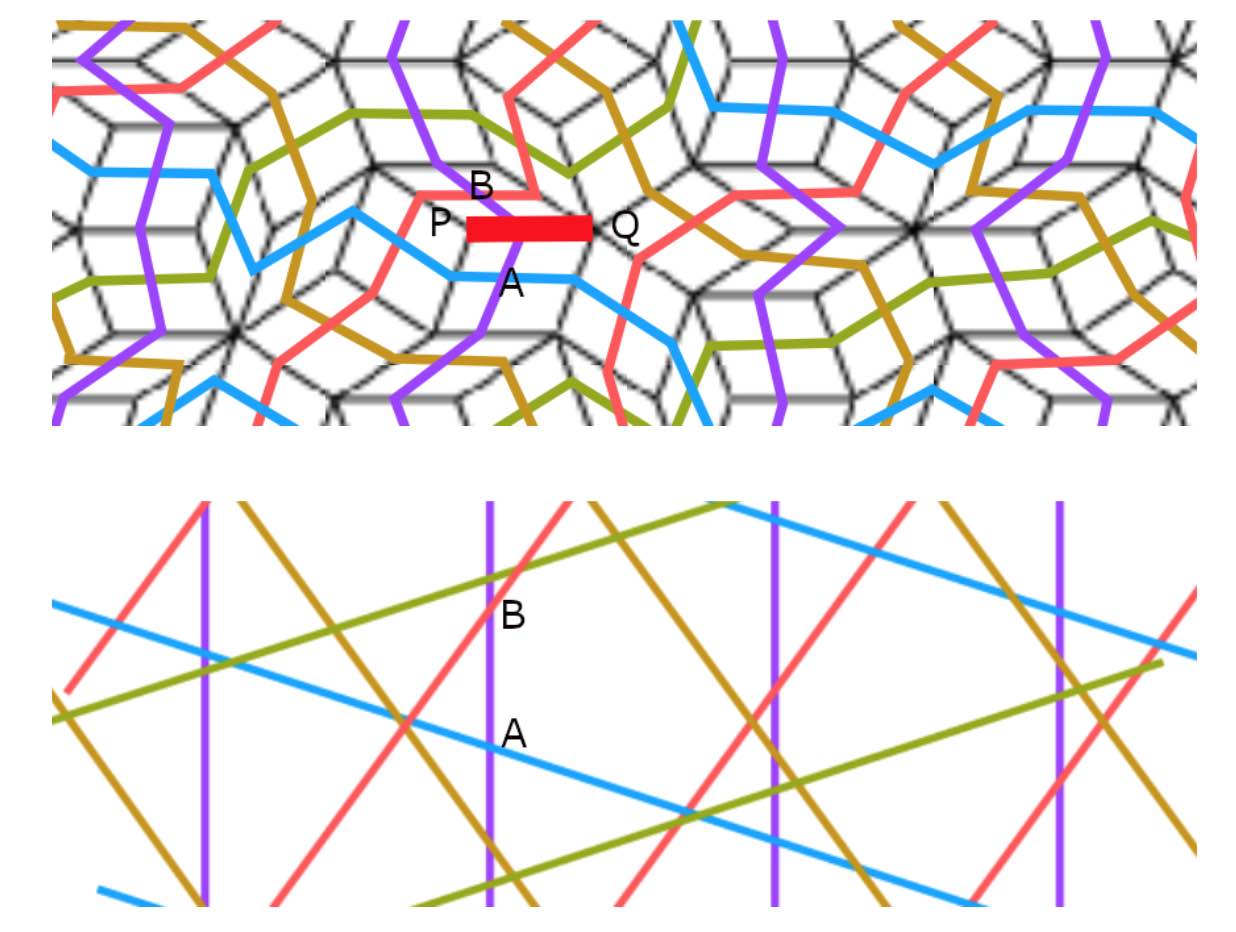
Last time we’ve seen that de Bruijn’s pentagrids determined the vertices of Penrose’s P3-aperiodic tilings.
These vertices can also be obtained by projecting a window of the standard hypercubic lattice $\mathbb{Z}^5$ by the cut-and-project-method.
We’ll bring in representation theory by forcing this projection to be compatible with a $D_5$-subgroup of the symmetries of $\mathbb{Z}^5$, which explains why Penrose tilings have a local $D_5$-symmetry.

The symmetry group of the standard $n$-dimensional hypercubic lattice
\[
\mathbb{Z} \vec{e}_1 + \dots + \mathbb{Z} \vec{e}_n \subset \mathbb{R}^n \]
is the hyperoctahedral group of all signed $n \times n$ permutation matrices
\[
B_n = C_2^n \rtimes S_n \]
in which all $n$-permutations $S_n$ act on the group $C_2^n = \{ 1,-1 \}^n$ of all signs. The signed permutation $n \times n$ matrix corresponding to an element $(\vec{a},\pi) \in B_n$ is given by
\[
T_{ij} = T(\vec{a},\pi)_{ij} = a_j \delta_{i,\pi(j)} \]
The represenation theory of $B_n$ was worked out in 1930 by the British mathematician and clergyman Alfred Young

We want to do explicit calculations in $B_n$ using a computational system such as
GAP, so it is best to describe $B_n$ as a permutation subgroup of $S_{2n}$ via the morphism
\[
\tau((\vec{a},\pi))(k) = \begin{cases} \pi(k)+n \delta_{-1,a_k}~\text{if $1 \leq k \leq n$} \\
\pi(k-n)+n(1-\delta_{-1,a_{k-n}})~\text{if $n+1 \leq k \leq 2n$} \end{cases} \]
the image is generated by the permutations
\[
\begin{cases}
\alpha = (1,2)(n+1,n+2), \\
\beta=(1,2,\dots,n)(n+1,n+2,\dots,2n), \\
\gamma=(n,2n)
\end{cases}
\]
and to a permutation $\sigma \in \tau(B_n) \subset S_{2n}$ we assign the signed permutation $n \times n$ matrix $T_{\sigma}=T(\tau^{-1}(\pi))$.
We use GAP to set up $B_5$ from these generators and determine all its conjugacy classes of subgroups. It turns out that $B_5$ has no less than $953$ different conjugacy classes of subgroups.
gap> B5:=Group((1,2)(6,7),(1,2,3,4,5)(6,7,8,9,10),(5,10));
Group([ (1,2)(6,7), (1,2,3,4,5)(6,7,8,9,10), (5,10) ])
gap> Size(B5);
3840
gap> C:=ConjugacyClassesSubgroups(B5);;
gap> Length(C);
953
But we are only interested in the subgroups isomorphic to $D_5$. So, first we make a sublist of all conjugacy classes of subgroups of order $10$, and then we go through this list one-by-one and look for an explicit isomorphism between $D_5 = \langle x,y~|~x^5=e=y^2,~xyx=y \rangle$ and a representative of the class (or get a ‘fail’ is this subgroup is not isomorphic to $D_5$).
gap> C10:=Filtered(C,x->Size(Representative(x))=10);;
gap> Length(C10);
3
gap> s10:=List(C10,Representative);
[ Group([ (2,5)(3,4)(7,10)(8,9), (1,5,4,3,2)(6,10,9,8,7) ]),
Group([ (1,6)(2,5)(3,4)(7,10)(8,9), (1,10,9,3,2)(4,8,7,6,5) ]),
Group([ (1,6)(2,7)(3,8)(4,9)(5,10), (1,2,8,4,10)(3,9,5,6,7) ]) ]
gap> D:=DihedralGroup(10);
gap> IsomorphismGroups(D,s10[1]);
[ f1, f2 ] -> [ (2,5)(3,4)(7,10)(8,9), (1,5,4,3,2)(6,10,9,8,7) ]
gap> IsomorphismGroups(D,s10[2]);
[ f1, f2 ] -> [ (1,6)(2,5)(3,4)(7,10)(8,9), (1,10,9,3,2)(4,8,7,6,5) ]
gap> IsomorphismGroups(D,s10[3]);
fail
gap> IsCyclic(s10[3]);
true
Of the three (conjugacy classes of) subgroups of order $10$, two are isomorphic to $D_5$, and the third one to $C_{10}$. Next, we have to transform the generating permutations into signed $5 \times 5$ permutation matrices using the bijection $\tau^{-1}$.
\[
\begin{array}{c|c}
\sigma & (\vec{a},\pi) \\
\hline
(2,5)(3,4)(7,10)(8,9) & ((1,1,1,1,1),(2,5)(3,4)) \\
(1,5,4,3,2)(6,10,9,8,7) & ((1,1,1,1,1)(1,5,4,3,2)) \\
(1,6)(2,5)(3,4)(7,10)(8,9) & ((-1,1,1,1,1),(2,5)(3,4)) \\
(1,10,9,3,2)(4,8,7,6,5) & ((-1,1,1,-1,1),(1,5,4,3,2))
\end{array}
\]
giving the signed permutation matrices
\[
\begin{array}{c|cc}
& x & y \\
\hline
A & \begin{bmatrix}
0 & 1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 \\
0 & 0 & 0 & 0 & 1 \\
1 & 0 & 0 & 0 & 0 \end{bmatrix} &
\begin{bmatrix} 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 1 & 0 \\
0 & 0 & 1 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 \end{bmatrix} \\
\hline
B & \begin{bmatrix}
0 & 1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & -1 & 0 \\
0 & 0 & 0 & 0 & 1 \\
-1 & 0 & 0 & 0 & 0 \end{bmatrix} &
\begin{bmatrix}
-1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 1 & 0 \\
0 & 0 & 1 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 \end{bmatrix}
\end{array}
\]
$D_5$ has $4$ conjugacy classes with representatives $e,y,x$ and $x^2$. the
character table of $D_5$ is
\[
\begin{array}{c|cccc}
& (1) & (2) & (2) & (5) \\
& 1_a & 5_1 & 5_2 & 2_a \\
D_5 & e & x & x^2 & y \\
\hline
T & 1 & 1 & 1 & 1 \\
V & 1 & 1 & 1 & -1 \\
W_1 & 2 & \tfrac{-1+ \sqrt{5}}{2} & \tfrac{-1 -\sqrt{5}}{2} & 0 \\
W_2 & 2 & \tfrac{-1 -\sqrt{5}}{2} & \tfrac{-1+\sqrt{5}}{2} & 0
\end{array}
\]
Using the signed permutation matrices it is easy to determine the characters of the $5$-dimensional representations $A$ and $B$
\[
\begin{array}{c|cccc}
D_5 & e & x & x^2 & y \\
\hline
A & 5 & 0 & 0 & 1 \\
B & 5 & 0 & 0 & -1
\end{array}
\]
decomosing into $D_5$-irreducibles as
\[
A \simeq T \oplus W_1 \oplus W_2 \quad \text{and} \quad B \simeq V \oplus W_1 \oplus W_2 \]
Representation $A$ realises $D_5$ as a rotation symmetry group of the hypercube lattice $\mathbb{Z}^5$ in $\mathbb{R}^5$, and next we have to find a $D_5$-projection $\mathbb{R}^5=A \rightarrow W_1 = \mathbb{R}^2$.
As a complex representation $A \downarrow_{C_5}$ decomposes as a direct sum of $1$-dimensional representations
\[
A \downarrow_{C_5} = V_1 \oplus V_{\zeta} \oplus V_{\zeta^2} \oplus V_{\zeta^3} \oplus V_{\zeta^4} \]
where $\zeta = e^{2 \pi i /5}$ and where the action of $x$ on $V_{\zeta^i}=\mathbb{C} v_i$ is given by $x.v_i = \zeta^i v_i$. The $x$-eigenvectors in $\mathbb{C}^5$ are
\[
\begin{cases}
v_0 = (1,1,1,1,1) \\
v_1 = (1,\zeta,\zeta^2,\zeta^3,\zeta^4) \\
v_2 =(1,\zeta^2,\zeta^4,\zeta,\zeta^3) \\
v_3 = (1,\zeta^3,\zeta,\zeta^4,\zeta^2) \\
v_4 = (1,\zeta^4,\zeta^3,\zeta^2,\zeta)
\end{cases}
\]
The action of $y$ on these vectors is given by $y.v_i = v_{5-i}$ because
\[
x.(y.v_i) = (xy).v_i=(yx^{-1}).v_i=y.(x^{-1}.v_i) = y.(\zeta^{-i} v_i) = \zeta^{-1} (y.v_i) \]
and therefore $y.v_i$ is an $x$-eigenvector with eigenvalue $\zeta^{5-i}$. As a complex $D_5$-representation, the factors of $A$ are therefore
\[
T = \mathbb{C} v_0, \quad W_1 = \mathbb{C} v_1 + \mathbb{C} v_4, \quad \text{and} \quad W_2 = \mathbb{C} v_2 + \mathbb{C} v_3 \]
But we want to consider $A$ as a real representation. As $\zeta^j = cos(\tfrac{2 \pi j}{5})+i~sin(\tfrac{2 \pi j}{5}) = c_j + i s_j$ hebben we can take the vectors in $\mathbb{R}^5$
\[
\begin{cases}
\frac{1}{2}(v_1+v_4) = (1,c_1,c_2,c_3,c_4)= u_1 \\
-\frac{1}{2}i(v_1-v_4) = (0,s_1,s_2,s_3,s_4) = u_2 \\
\frac{1}{2}(v_2+v_3) = (1,c_2,c_4,c1,c3)= w_1 \\
-\frac{1}{2}i(v_2-v_3) = (0,s_2,s_4,s_1,s_3)= w_2
\end{cases}
\]
and $A$ decomposes as a real $D_5$-representation with
\[
T = \mathbb{R} v_0, \quad W_1 = \mathbb{R} u_1 + \mathbb{R} u_2, \quad \text{and} \quad W_2 = \mathbb{R} w_1 + \mathbb{R} w_2 \]
and if we identify $\mathbb{C}$ with $\mathbb{R}^2$ via $z \leftrightarrow (Re(z),Im(z))$ we can describe the $D_5$-projection morphism $\pi_{W_1}~:~\mathbb{R}^5=A \rightarrow W_1=\mathbb{R}^2$ via
\[ (y_0,y_1,y_2,y_3,y_4) \mapsto y_0+y_1 \zeta + y_2 \zeta^2 + y_3 \zeta^3 + y_4 \zeta^4 = \sum_{i=0}^4 y_i (c_i,s_i) \]
Note also that $W_1$ is the orthogonal complement of $T \oplus W_2$, so is equal to the linear subspace in $\mathbb{R}^5$ determined by the three linear equations
\[
\begin{cases}
\sum_{i=0}^4 x_i = 0 \\
\sum_{i=0}^4 c_{2i} x_i = 0 \\
\sum_{i=0}^4 s_{2i} x_i = 0
\end{cases}
\]

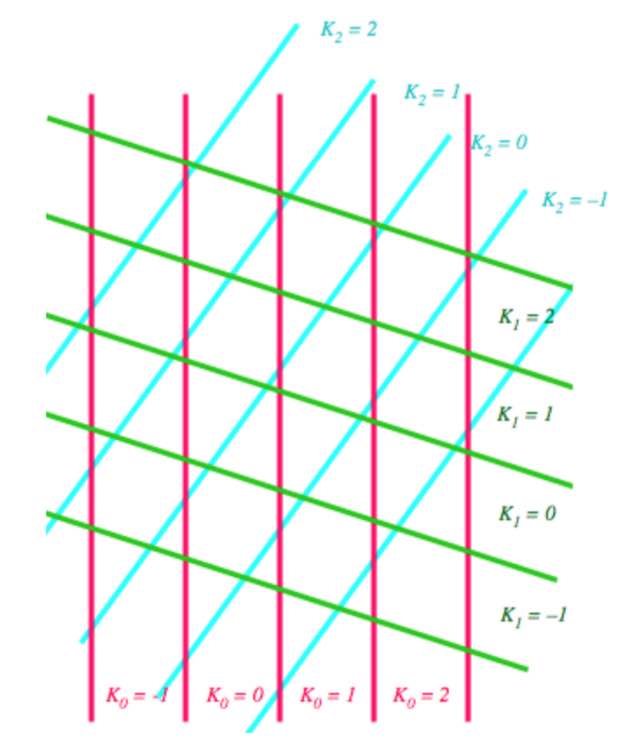
Okay, now take the Rhombic tiling corresponding to the regular pentagrid defined by $\gamma_0, \dots, \gamma_4$ satisfying $\sum_{i=0}^4 \gamma_i = 0$. Let $\vec{k}=(k_0,\dots,k_4) \in \mathbb{Z}^5$ and define the
open hypercube $H_{\vec{k}}$ corresponding to $\vec{k}$ as the set of points
\[
(x_0,\dots,x_4) \in \mathbb{R}^5~:~\forall 0 \leq i \leq 4~:~k_i – 1 < x_i < k_i \]
From the vector $\vec{\gamma} = (\gamma_0,\dots,\gamma_4)$ determining the Rhombic tiling we define the $2$-dimensional plane $P_{\vec{\gamma}}$ in $\mathbb{R}^5$ given by the equations
\[
\begin{cases}
\sum_{i=0}^4 x_i = 0 \\
\sum_{i=0}^4 c_{2i} (x_i - \gamma_i) = 0 \\
\sum_{i=0}^4 s_{2i} (x_i - \gamma_i) = 0
\end{cases}
\]
The point being that $P_{\vec{\gamma}}$ is the linear plane $W_1$ in $\mathbb{R}^5$ translated over the vector $\vec{\gamma}$, so it is parallel to $W_1$. Here's the punchline:
de Bruijn’s theorem: The vertices of the Rhombic tiling produced by the regular pentagrid with parameters $\vec{\gamma}=(\gamma_0,\dots,\gamma_4)$ are the points
\[
\sum_{i=0}^4 k_i (c_i,s_i) \]
with $\vec{k}=(k_0,\dots,k_4) \in \mathbb{Z}^5$ such that $H_{\vec{k}} \cap P_{\vec{\gamma}} \not= \emptyset$.
To see this, let $\vec{x} = (x_0,\dots,x_4) \in P_{\vec{\gamma}}$, then $\vec{x}-\vec{\gamma} \in W_1$, but then there is a vector $\vec{y} \in \mathbb{R}^2$ such that
\[
x_j – \gamma_j = \vec{y}.\vec{v}_j \quad \forall~0 \leq j \leq 4 \]
But then, with $k_j=\lceil \vec{y}.\vec{v}_j + \gamma_j \rceil$ we have that $\vec{x} \in H_{\vec{k}}$ and we note that $V(\vec{y}) = \sum_{i=0}^4 k_i \vec{v}_i$ is a vetex of the Rhombic tiling associated to the regular pentagrid parameters $\vec{\gamma}=(\gamma_0,\dots,\gamma_4)$.
Here we used regularity of the pentagrid in order to have that $k_j=\vec{y}.\vec{v}_j + \gamma_j$ can happen for at most two $j$’s, so we can manage to vary $\vec{y}$ a little in order to have $\vec{x}$ in the open hypercube.
Here’s what we did so far: we have identified $D_5$ as a group of rotations in $\mathbb{R}^5$, preserving the hypercube-lattice $\mathbb{Z}^5$ in $\mathbb{R}^5$. If the $2$-plane $P_{\vec{\gamma}}$ is left stable under these rotations, then because rotations preserve distances, also the subset of lattice-points
\[
S_{\vec{\gamma}} = \{ (k_0,\dots,k_4)~|~H_{\vec{k}} \cap P_{\vec{\gamma}} \not= \emptyset \} \subset \mathbb{Z}^5 \]
is left stable under the $D_5$-action. But, because the map
\[
(k_0,\dots,k_4) \mapsto \sum_{i=0}^4 k_i (c_i,s_i) \]
is the $D_5$-projection map $\pi : A \rightarrow W_1$, the vertices of the associated Rhombic tiling must be stable under the $D_5$-action on $W_1$, meaning that the Rhombic tiling should have a global $D_5$-symmetry.
Sadly, the only plane $P_{\vec{\gamma}}$ left stable under all rotations of $D_5$ is when $\vec{\gamma} = \vec{0}$, which is an
exceptionally singular pentagrid. If we project this situation we do indeed get an image with global $D_5$-symmetry

but it is
not a Rhombic tiling. What’s going on?
Because this post is already dragging on for far too long (TL;DR), we’ll save the investigation of projections of singular pentagrids, how they differ from the regular situation, and how they determine multiple Rhombic tilings, for another time.