Last year we managed to solve the first few riddles of the Bourbaki code, but several mysteries still remain. For example, who was the priest performing the Bourbaki-Petard wedding ceremony? The ‘faire part’ identifies him as ‘le P. Adique, de l’Ordre des Diophantiens’.

As with many of these Bourbaki-jokes, this riddle too has several layers. There is the first straightforward mathematical interpretation of the p-adic numbers $latex \hat{\mathbb{Z}}_p$ being used in the study of Diophantine problems.
 For example, the local-global, or Hasse principle, asserting that an integral quadratic form has a solution if and only if there are solutions over all p-adic numbers. Helmut Hasse was a German number theorist, held in high esteem by the Bourbaki group.
For example, the local-global, or Hasse principle, asserting that an integral quadratic form has a solution if and only if there are solutions over all p-adic numbers. Helmut Hasse was a German number theorist, held in high esteem by the Bourbaki group.
After graduating from the ENS in 1929, Claude Chevalley spent some time at the University of Marburg, studying under Helmut Hasse. Hasse had come to Marburg when Kurt Hensel (who invented the p-adic numbers in 1902) retired in 1930.
Hasse picked up a question from E. Artin’s dissertation about the zeta function of an algebraic curve over a finite field and achieved the first breakthrough establishing the conjectured property for zeta functions of elliptic curves (genus one).
Extending this result to higher genus was the principal problem Andre Weil was working on at the time of the wedding-card-joke. In 1940 he would be able to settle the general case. What we now know as the Hasse-Weil theorem implies that the number N(p) of rational points of an elliptic curve over the finite field Z/pZ, where p is a prime, can differ from the mean value p+1 by at most twice the square root of p.
So, Helmut Hasse is a passable candidate for the first-level, mathematical, decoding of ‘le P. adique’.
However, there is often a deeper and more subtle reading of a Bourbaki-joke, intended to be understood only by the select inner circle of ‘normaliens’ (graduates of the Ecole Normale Superieure). Usually, this second-level interpretation requires knowledge of events or locations within the 5-th arrondissement of Paris, the large neighborhood of the ENS.
For an outsider (both non-Parisian and non-normalien) decoding this hidden message is substantially harder and requires a good deal of luck.
As it happens, I’m going through a ‘Weil-phase’ and just started reading the three main Weil-biographies : Andre Weil the Apprenticeship of a Mathematician, Chez les Weil : André et Simone by Sylvie Weil and La vie de Simone Weil by Simone Petrement.
[abp:3764326506] [abp:2283023696] [abp:2213599920]
From page 35 of ‘Chez les Weil’ : “Après la guerre, pas tout de suite mais en 1948, toute la famille avait fini par revenir à Paris, rue Auguste-Comte, en face des jardins du Luxembourg.” Sylvie talks about the Parisian apartment of her grandparents (father and mother of Andre and Simone) and I wanted to know its exact location.
More details are given on page 103 of ‘La vie de Simone Weil’. The apartment consists of the 6th and 7th floor of a building on the Montagne Sainte-Geneviève. The Weils bought it before it was even built and when they moved in, in may 1929, it was still unfinished. Compensating this, the apartment offered a splendid view of the Sacre-Coeur, the Eiffel-tower, la Sorbonne, Invalides, l’Arc de Triomphe, Pantheon, the roofs of the Louvre, le tout Paris quoi…
As to its location : “Juste au-dessous de l’appartement se trouvent l’Ecole des mines et les serres du Luxembourg, avec la belle maison ancienne où mourut Leconte de Lisle.” This and a bit of googling allows one to deduce that the Weils lived at 3, rue Auguste-Comte (the W on the map below).
 Crossing the boulevard Saint-Michel, one enters the 5-th arrondissement via the … rue de l’Abbe de l’Epee…
Crossing the boulevard Saint-Michel, one enters the 5-th arrondissement via the … rue de l’Abbe de l’Epee…
We did deduce before that the priest might be an abbot (‘from the order of the Diophantines’) and l’Epee is just ‘le P.’ pronounced in French (cheating one egue).
Abbé Charles-Michel de l’Épée lived in the 18th century and has become known as the “Father of the Deaf” (compare this to Diophantus who is called “Father of Algebra”). Épée turned his attention toward charitable services for the poor, and he had a chance encounter with two young deaf sisters who communicated using a sign language. Épée decided to dedicate himself to the education and salvation of the deaf, and, in 1760, he founded a school which became in 1791 l’Institution Nationale des Sourds-Muets à Paris. It was later renamed the Institut St. Jacques (compare Rue St. Jacques) and then renamed again to its present name: Institut National de Jeunes Sourds de Paris located at 254, rue Saint-Jacques (the A in the map below) just one block away from the Schola Cantorum at 269, rue St. Jacques, where the Bourbaki-Petard wedding took place (the S in the map).
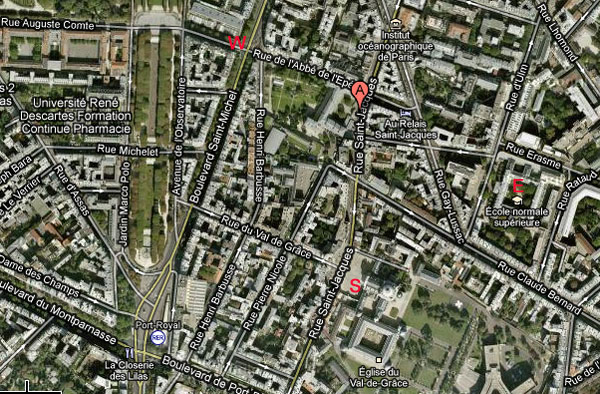
Completing the map with the location of the Ecole Normale (the E) I was baffled by the result. If the Weil apartment stands for West, the Ecole for East and the Schola for South, surely there must be an N (for N.Bourbaki?) representing North. Suggestions anyone?
Comments