In according to Groth IV.22 we tried to solve one of the riddles contained in Roubaud’s announcement of Bourbaki’s death.
Today, we’ll try our hands on the next one: where was Bourbaki buried?
The death announcement gives this fairly opaque clue:
“The burial will take place in the cemetery for Random Functions (metro stations Markov and Gödel) on Saturday, November 23, 1968 at 3 o’clock in the afternoon.”
What happened on November 23rd 1968?

Bourbaki died on November 11th, 1968 (exactly 50 years after the end of WW1). Perhaps an allusion to the mandatory retirement age for members of Bourbaki, as suggested by the Canulars Bourbaki.
Be that as it may, I believe this date was chosen because it is conveniently close to the intended time of the burial.
But then, what’s so special about November 23rd, 1968?
Well, is there a more suitable moment to burry Bourbaki than during a Seminaire Bourbaki? And, yes, in the fall of 1968 the seminar was organised from saturday 23rd till monday 25th of november:

So, where would all of Bourbaki’s close family be at 3 o’clock on that particular saturday? Right, at l’Institut Henri Poincare.
But, it’s hard to view the IHP as a cemetery. Besides, it’s nowhere close to two metro stations as a quick look on the map shows. The closest one is the RER-station at the Luxembourg gardens, but the RER-line didn’t exist in 1968.
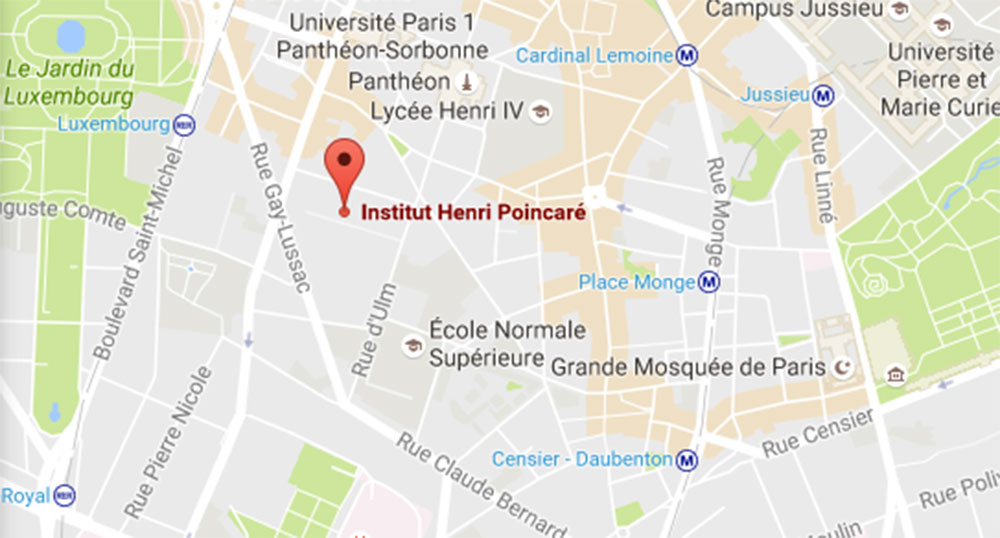
(True Parisians may object that the Gare du Luxembourg was at the time the terminus of the Ligne de Sceaux which has a fascinating history, but let’s try to remain on track…)
If the first clue is the Institut Henri Poincare, then if we are looking for a cemetery, we might ask:
Where’s Poincare’s tomb?

Jules Henri Poincare is burried in the family tomb at the Montparnasse cemetery

He’s not the only mathematician buried there. Évariste Galois, Jean Victor Poncelet, Joseph Liouville, Charles Hermite, and Gaston Darboux also found their last resting place in Montparnasse.
In fact, there are at least 104 mathematicians buried at Montparnasse.
This is hardly surprising as the Montparnasse cemetery is close to the IHP, the Collège de France, the Sorbonne, the “rue d’Ulm” aka the ENS, l’Observatoire and until 1976 l’École polytechnique.
Here’s a map with pointers to some of these tombs:
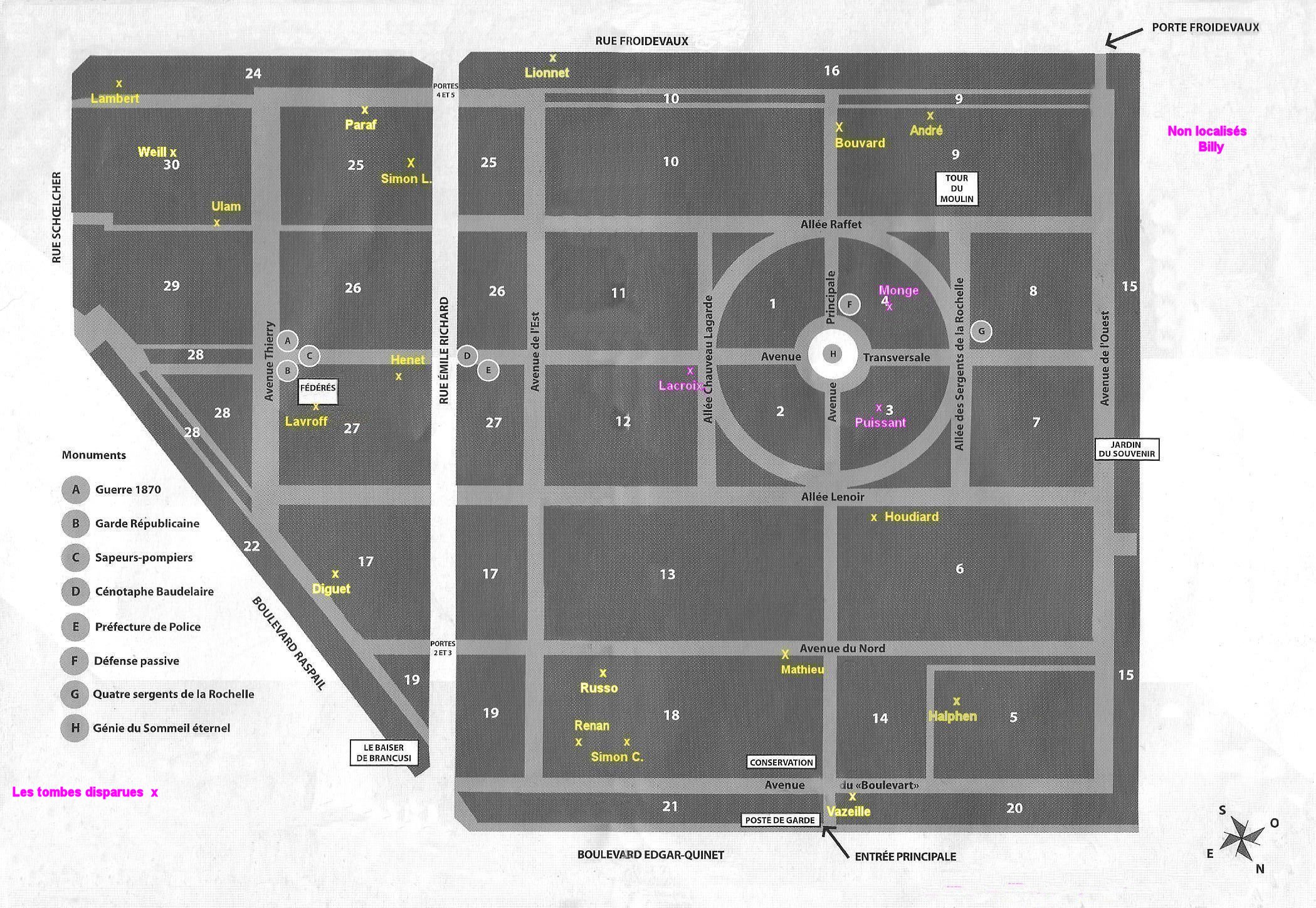
So, the Montparnasse cemetery appears to be a plausible place to host Bourbaki’s tomb.
But, what about the other “clues”?
“Cemetery of random functions (metro stations Markov and Gödel)”
There are several references lo logic, set theory and applied mathematics in Bourbaki’s death announcement. Why?
Roubaud (and many with him) feel that the Bourbaki enterprise failed miserably in these areas.
He writes on page 49 of his book Mathematics, a novel:
“But Bourbaki, that ‘collective mathematician”, as Raymond Queneau put it, also had a good knowledge of the current state of mathematics at the time when his Treatise was being composed; with, of course, a few “gaps”:
for example, probability, which was considered to be just an “applied” brand of measure theory”; and logic, especially logic, which was made almost a pariah because of (so it was rumored) the premature death of Herbrand, who, in the generation of founders, Normaliens to a man, had studied under Hilbert, and thus had been associated with his meteoric rise; in sum, logic had died in a climbing accident along with Herbrand.”
This might explain the cemetery of “random functions” and the metro stations named after the logicians and set theorists Kurt Gödel and A.A. Markov or the father of stochastic processes Andrey Markov.
Is there more into these references?
Probably not, but just to continue with our silly game, the two metro stations closest to the Montparnasse cemetery are Raspail and Edgar Quinet.
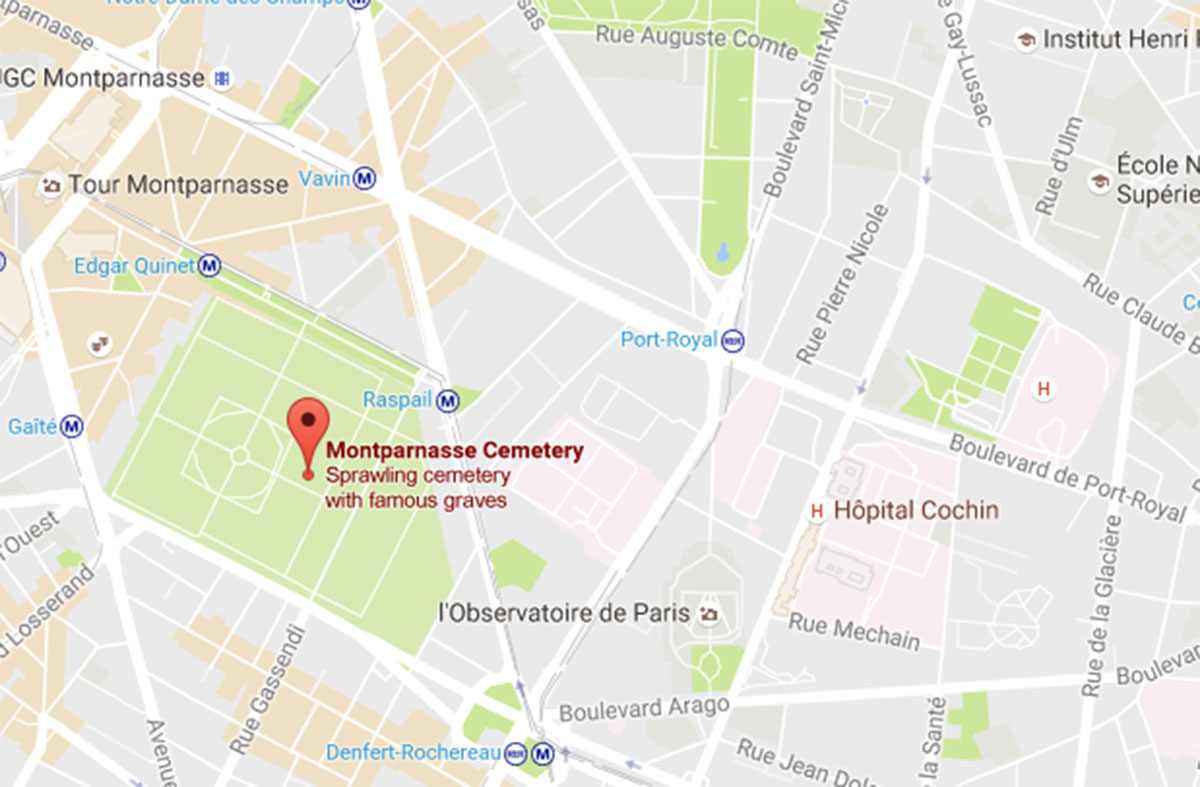
Now, François-Vincent Raspail was a French chemist, naturalist, physician, physiologist, attorney, and socialist politician.
More relevant to our quest is that the Centre d’analyse et de mathématique sociales (CAMS) was based at 54, boulevard Raspail. The mission statement on their website tells that this institute is clearly devoted to all applications of mathematics. That is, “Raspail” may be another pointer to applied mathematics and random functions.
As for the other metro station, Edgar Quinet was a French historian and intellectual. Is there a connection to logic or set theory? Well, sort of. The Encyclopedia Britannica has this to say about Edgar Quinet:
“His rhetorical power was altogether superior to his logical power, and the natural consequence is that his work is full of contradictions.”
I rest my case.
Comments