the Riemann hypothesis and 5040

Yesterday, there was an interesting post by John Baez at the n-category cafe: The Riemann Hypothesis Says 5040 is the Last.

The 5040 in the title refers to the largest known counterexample to a bound for the sum-of-divisors function
\[
\sigma(n) = \sum_{d | n} d = n \sum_{d | n} \frac{1}{d} \]

In 1983, the french mathematician Guy Robin proved that the Riemann hypothesis is equivalent to
\[
\frac{\sigma(n)}{n~log(log(n))} < e^{\gamma} = 1.78107... \] when $n > 5040$.

The other known counterexamples to this bound are the numbers 3,4,5,6,8,9,10,12,16,18,20,24,30,36,48,60,72,84,120,180,240,360,720,840,2520.

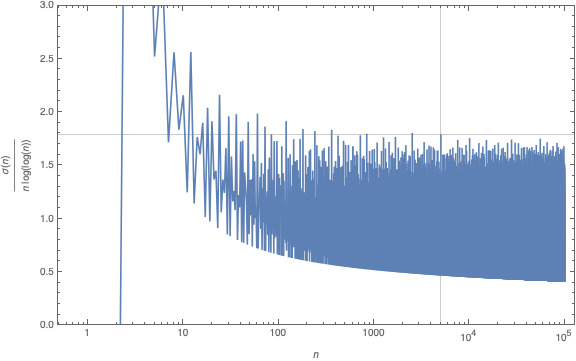
In Baez’ post there is a nice graph of this function made by Nicolas Tessore, with 5040 indicated with a grey line towards the right and the other counterexamples jumping over the bound 1.78107…



Robin’s theorem has a remarkable history, starting in 1915 with good old Ramanujan writing a part of this thesis on “highly composite numbers” (numbers divisible by high powers of primes).

His PhD. adviser Hardy liked his result but called them “in the backwaters of mathematics” and most of it was not published at the time of Ramanujan’s degree ceremony in 1916, due to paper shortage in WW1.

When Ramanujan’s paper “Highly Composite Numbers” was first published in 1988 in ‘The lost notebook and other unpublished papers’ it became clear that Ramanujan had already part of Robin’s theorem.

Ramanujan states that if the Riemann hypothesis is true, then for $n_0$ large enough we must have for all $n > n_0$ that
\[
\frac{\sigma(n)}{n~log(log(n))} < e^{\gamma} = 1.78107... \] When Jean-Louis Nicolas, Robin's PhD. adviser, read Ramanujan's lost notes he noticed that there was a sign error in Ramanujan's formula which prevented him from seeing Robin's theorem.

Nicolas: “Soon after discovering the hidden part, I read it and saw the difference between Ramanujan’s result and Robin’s one. Of course, I would have bet that the error was in Robin’s paper, but after recalculating it several times and asking Robin to check, it turned out that there was an error of sign in what Ramanujan had written.”

If you are interested in the full story, read the paper by Jean-Louis Nicolas and Jonathan Sondow: Ramanujan, Robin, Highly Composite Numbers, and the Riemann Hypothesis.

What’s the latest on Robin’s inequality? An arXiv-search for Robin’s inequality shows a flurry of activity.

For starters, it has been verified for all numbers smaller that $10^{10^{13}}$…

It has been verified, unconditionally, for certain classes of numbers:

• all odd integers $> 9$
• all numbers not divisible by a 25-th power of a prime

Rings a bell? Here’s another hint:

According to Xiaolong Wu in A better method than t-free for Robin’s hypothesis one can replace the condition of ‘not divisible by an N-th power of a prime’ by ‘not divisible by an N-th power of 2’.

Further, he claims to have an (as yet unpublished) argument that Robin’s inequality holds for all numbers not divisible by $2^{42}$.

So, where should we look for counterexamples to the Riemann hypothesis?

What about the orders of huge simple groups?

The order of the Monster group is too small to be a counterexample (yet, it is divisible by $2^{46}$).