We know embarrassingly little about the symmetries of the roots of all polynomials with rational coefficients, or if you prefer, the absolute Galois group $Gal(\overline{\mathbb{Q}}/\mathbb{Q})$.
In the title picture the roots of polynomials of degree $\leq 4$ with small coefficients are plotted and coloured by degree: blue=4, cyan=3, red=2, green=1. Sums and products of roots are again roots and by a symmetry we mean a map on all roots, sending sums to sums and products to products and leaving all the green dots (the rational numbers) fixed.
John Baez has an excellent post on the beauty of roots, including a picture of all polynomials of degree $\leq 5$ with integer coefficients between $-4$ and $4$ and, this time, colour-coded by: grey=2, cyan=3, red=4 and black=5.
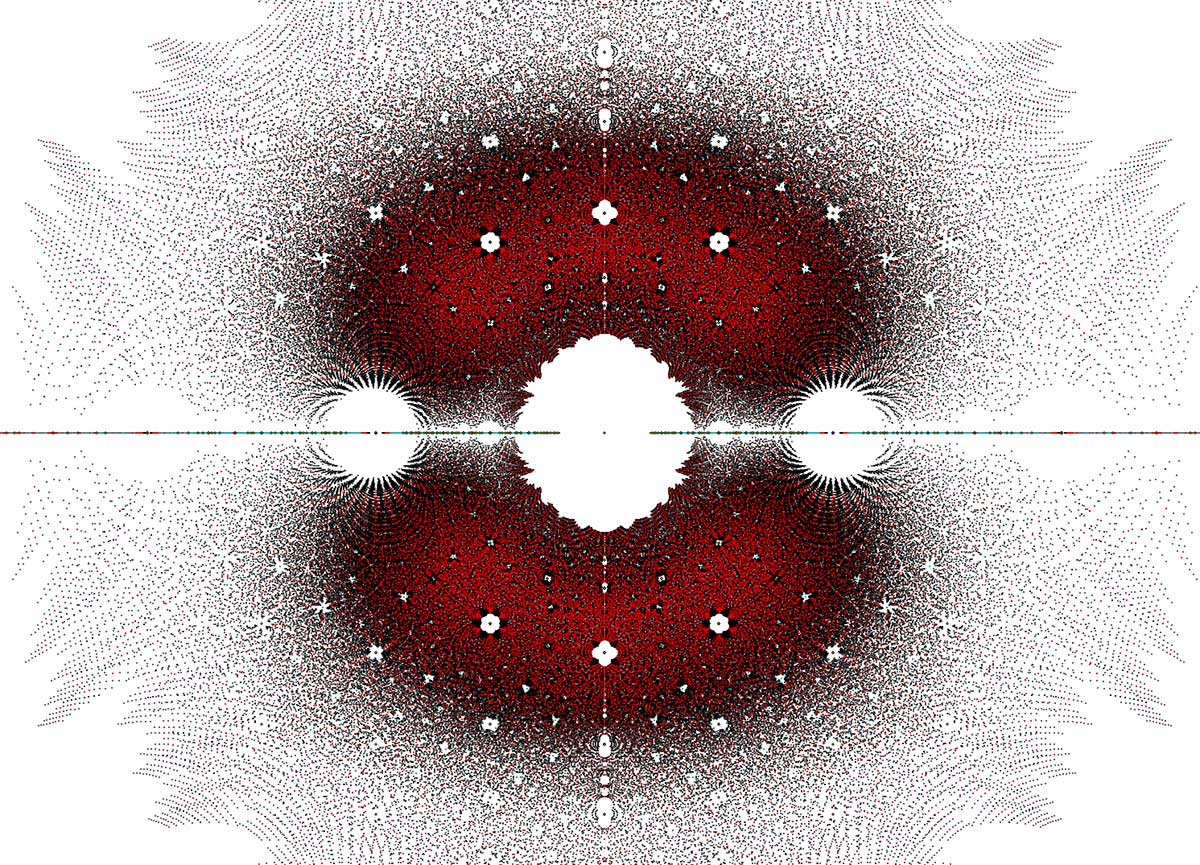
In both pictures there’s a hint of the unit circle, black in the title picture and spanning the ‘white gaps’ in the picture above.
If we’d only consider the sub-picture of all (sums and products of) roots including the rational numbers on the horizontal axis and the roots of unity on the unit circle we’d get the cyclotomic field $\mathbb{Q}_{cyc} = \mathbb{Q}(\mu_{\infty})$. Here we know all symmetries: they are generated by taking powers of the roots of unity. That is, we know all about the Galois group $Gal(\mathbb{Q}_{cyc}/\mathbb{Q})$.
The ‘missing’ symmetries, that is the Galois group $Gal(\overline{\mathbb{Q}}/\mathbb{Q}_{cyc})$ remained a deep mystery, until last week…
[section_title text=”The oracle speaks”]
On september 15th, Robert Kucharczyk and Peter Scholze (aka the “oracle of arithmetic” according to Quanta-magazine) arXived their paper Topological realisations of absolute Galois groups.
They discovered a concrete compact connected Hausdorff space $M_{cyc}$ such that Galois extensions of $\mathbb{Q}_{cyc}$ correspond to connected etale covers of $M_{cyc}$.
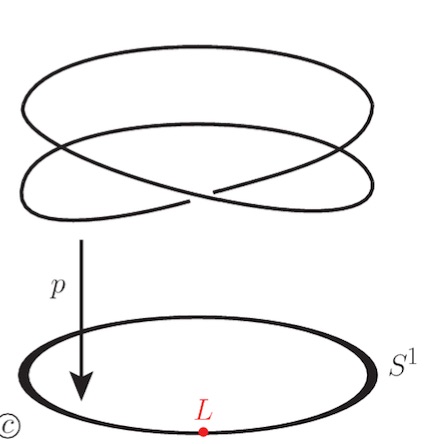Let’s look at a finite field $\mathbb{F}_p$. Here, Galois extensions of $\mathbb{F}_p$ (and there is just one such extension of degree $n$, upto isomorphism) correspond to connected etale covers of the circle $S^1$.
An etale map $X \rightarrow S^1$ is such that every circle point has exactly $n$ pre-images. Here again, up to homeomorphism, there is a unique such $n$-fold cover of $S^1$ (the picture on the left gives the cover for $n=2$).
.
If we replace $\mathbb{F}_p$ by the cyclotomic field $\mathbb{Q}_{cyc}$ then the compact space $M_{cyc}$ replaces the circle $S^1$. So, if we take a splitting polynomial of degree $n$ with coefficients in $\mathbb{Q}_{cyc}$, then there is a corresponding etale $n$-fold cover $X \rightarrow M_{cyc}$ such that for a specific point $p$ in $M_{cyc}$ its pre-images correspond to the roots of the polynomial. Nice!
Sadly, there’s a catch. Even though we have a concrete description of $M_{cyc}$ it turns out to be a horrible infinite dimensional space, it is connected but not path-connected, and so on.
Even Peter Scholze says it’s unclear whether new results can be proved from this result (see around 39.15 in his Next Generation Outreach Lecture).
Btw. if your German is ok, this talk is a rather good introduction to classical Galois theory and etale fundamental groups, including the primes=knots analogy.
[section_title text=”the imaginary field with one element”]
Of course there’s no mention of it in the Kucharczyk-Scholze paper, but this result is excellent news for those trying to develop a geometry over the imaginary field with one element $\mathbb{F}_1$ and hope to apply this theory to problems in number theory.
As a side remark, some of these people have just published a book with the EMS Publishing House: Absolute arithmetic and $\mathbb{F}_1$-geometry
The basic idea is that the collection of all prime numbers, $\mathbf{Spec}(\mathbb{Z})$ is far too large an object to be a terminal object (as it is in schemes). One should therefore extend the setting of schemes to so called $\mathbb{F}_1$-schemes, in which $\mathbf{Spec}(\mathbb{Z})$ is some higher dimensional object.
Initially, one hoped that $\mathbf{Spec}(\mathbb{Z})/\mathbb{F}_1$ might look like a curve, so that one could try to mimick Weil’s proof of the Riemann hypothesis for curves to prove the genuine Riemann hypothesis.
But, over the last decade it became clear that $\mathbf{Spec}(\mathbb{Z})/\mathbb{F}_1$ looks like an infinite dimensional space, a bit like the space $M_{cyc}$ above.
I’ll spare this to a couple of follow-up posts, but for now I’ll leave you with the punchline:
The compact connected Hausdorff space $M_{cyc}$ of Kucharczyk and Scholze is nothing but the space of complex points of $\mathbf{Spec}(\mathbb{Q}_{cyc})/\mathbb{F}_1$!
One Comment