To most mathematicians, a good LaTeX-frontend (such as TeXShop for Mac-users) is the crucial tool to get the work done. We use it to draft ideas, write papers and courses, or even to take notes during lectures.
However, after six years of blogging, my own LaTeX-routine became rusty. I rarely open a new tex-document, and when I do, I’d rather copy-paste the long preamble from an old file than to start from scratch with a minimal list of packages and definitions needed for the job at hand. The few times I put a paper on the arXiv, the resulting text resembles a blog-post more than a mathematical paper, here’s an example.
As I desperately need to get some math-writing done, I need to pull myself away from the lure of an ever-open WordPress admin browser-screen and reacquaint myself with the far more efficient LaTeX-environment.
Perhaps even my blogging will benefit from the change. Whereas I used to keep on adding to most of my tex-files in order to keep them up-to-date, I rarely edit a blog-post after hitting the ’publish’ button. If I really want to turn some of my better posts into a book, I need them in a format suitable for neverending polishing, without annoying the many RSS-feed aggregators out there.
Who better than Terry Tao to teach me a more proficient way of blogging? A few days ago, Terry announced he will soon have his 5th (!!) book out, after three years of blogging…
How does he manage to do this? Well, as far as I know, Terry blogs in LaTeX and then uses a python-script called LaTeX2WP ’a program that converts a LaTeX file into something that is ready to be cut and pasted into WordPress. This way, you can write, and preview, your post in LaTeX, then run LaTeX2WP, and post into WordPress whatever comes out.’ More importantly, one retains a pure-tex-file of the post on which one can keep on editing to get it into a (book)-publishable form, eventually.
Nice, but one can do even better, as Eric from Curious Reasoning worked out. He suggests to install two useful python-packages : WordPressLib “with this library you can control remotely a WordPress installation. Use of library is very simple, you can write a small scripts or full applications that allows you to automate publishing of articles on your blog/site powered by WordPress” and plasTeX “plasTeX is a LaTeX document processing framework written entirely in Python. It currently comes bundled with an XHTML renderer (including multiple themes), as well as a way to simply dump the document to a generic form of XML”. Installation is easy : download and extract the files somewhere, go there and issue a **sudo python setup.py install** to add the packages to your python.
Finally, get Eric’s own wplatex package and install it as explained there. WpLaTeX has all the features of LaTeX2WP and much more : one can add titles, tags and categories automatically and publish the post from the command-line without ever having to enter the taboo WordPress-admin page! Here’s what I’ve written by now in TeXShop
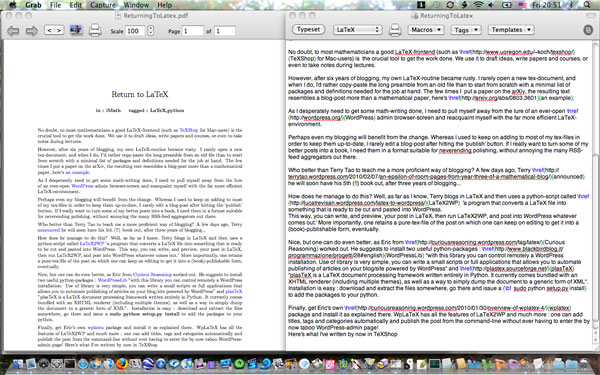
I’ve added the screenshot and the script will know where to find it online for the blog-version as well as on my hard-disk for the tex-version. Very handy is the iftex … fi versus ifblog … fi alternative which allows you to add pure HTML to get the desired effect, when needed. Remains only to go into Terminal and issue the command
wplpost -x http://www.neverendingbooks.org/xmlrpc.php ReturnToLatex.tex
(if your blog is on WordPress.com it even suffices to give its name, rather than this work-around for stand-alone wordpress blogs). The script asks for my username and password and will convert the tex-file and post it automatic.


