Tag: tilings

Before we’ll come to applications of quasicrystals to viruses it is perhaps useful to illustrate essential topics such as deflation, inflation, aperiodicity, local isomorphism and the cut-and project method in the simplest of cases, that of $1$-dimensional tilings.

We want to tile the line $\mathbb{R}^1$ with two kinds of tiles, short ($S$) and ($L$) long intervals, differing by a golden ratio factor $\tau=\tfrac{1}{2}(1+\sqrt{5}) \approx 1.618$.

Clearly, no two tiles may overlap and we impose a gluing restriction: there can be no two consecutive $S$-intervals in the tiling, and no three consecutive $L$-intervals.

The code of a tiling is a doubly infinite word in $S$ and $L$ such that there are no two consecutive $S$’s nor three consecutive $L$’s. For example
\[
\sigma = \dots LSLLSLS\underline{L}LSLLSL \dots \]
We underline one tile to distinguish the sequence from shifts of it.

Conway’s musical sequences will be special codes (or tilings), allowing for the inverse operations of inflation and deflation, terms coined by John Conway in relation to Penrose tilings. The musical sequences are important to understand Conway’s worms (sometimes called “wormholes”) which are strings of Long and Short bow ties in a Penrose tiling, and to measure the distances between Amman bars. In fact, many of the properties of Penrose tilings and $3$-dimensional quasicrystals (for example, local isomorphism) have their counterparts for tilings having a musical sequence as code.

Conway’s investigations of Penrose tiles held up work on the ATLAS-project and caused some problems at home:

“In pursuing his investigations, he unsurped some of his wife Eileen’s territory, covering the dining table with an infinite nuisance of tiles. He cut them out himself, causing his right hand to hurt with cramps for days. To Eileen’s dismay, he studied the dining table mosaic for a year, relegating family meals to the kitchen and prohibiting dinner parties.”

From “Genius at Play – The curious mind of John Horton Conway” by Siobhan Roberts

Let’s investigate inflation and deflation of these tilings.

The point of the golden factor $\tau$ is to allow for deflation. That is, we can replace a tiling by another one with tiles $S$ and $L$ both a factor $\tfrac{1}{\tau}=\tau-1 \approx 0.618$ smaller than the original tiles. If the original $S$-tile has length $a$ (and the $L$-tile length $\tau a$), then the new tile $S$ wil have length $\tfrac{1}{\tau}a$ and the new $L$-tile length $a$.
We do this by replacing each old $S$-tile by a new $L$-tile, and to break up any old $L$-tile in a new $L$ and new $S$-tile, as $\tau a = a + \tfrac{1}{\tau}a$ (note that $\tau^2=\tau+1$)

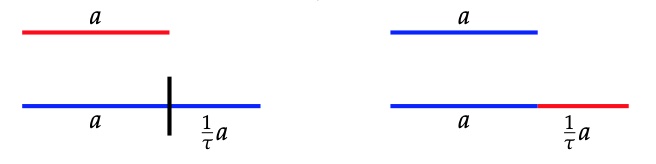
To get the code of the deflated tiling we replace each letter $S$ by a letter $L$ and each $L$ by $LS$. The underlined letter will be the first letter of the deflated underlined letter in the original sequence. The deflated sequence of the one above is
\[
def(\sigma) = \dots LSLLSLSLLSL\underline{L}SLSLLSLSLLS \dots \]
and it is easy to see that the deflated tiling satisfies again the gluing condition.

Certain of these tilings (not all!) allow for an inverse to deflation, called inflation, increasing the size of the tiles by a factor $\tau$.

Starting from a tiling we divide each $L$-tile in half and these mid-points will be end-points of the tiles in the new tiling, erasing all endpoints of the original one. The inflated tiling will have two sorts of tiles, a new short one $S$ of length $\tau a$ obtained from the end-half of an original $L$-tile, followed b the start-half of an original $L$-tile, and a new long tile $L$ of length $\tau^2 a = (\tau+1) a$, made of the end-half of an original $L$, followed by an original $S$, followed by the start-half of an original $L$.

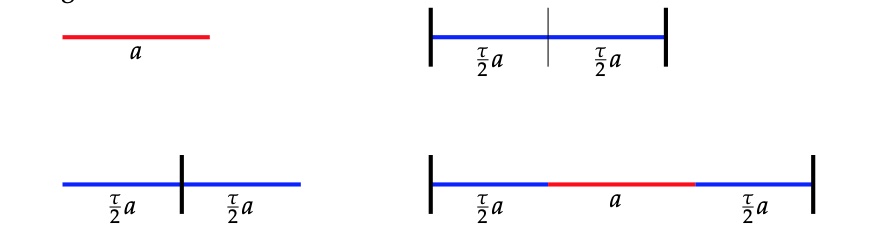
We get the code of the inflated tiling by replacing first each $L$ by $ll$ and subsequently replace each word $lSl$ by a letter $L$ and each $ll$ by $S$. An example,
\[
\sigma = \dots LSLLSLSLLSL\underline{L}SLSLLSLSLLS \dots \\
\dots llSllllSllSllllSlll\underline{l}SllSllllSllSllllS \dots \\
inf(\sigma) = \dots (l)LSLLSLS\underline{L}LSLLS(lS) \dots \]

But, the inflated tiling may no longer satisfy the gluing condition. An example
\[
\dots LSLSLSL \dots \mapsto \dots llSllSllSll \dots \mapsto \dots (l)LLL(l) \dots \]

A Conway musical sequence is the code of a tiling $\sigma$ such that all its consecutive inflations $inf^n(\sigma)$ satisfy the gluing condition. For the corresponding Conway tiling $\sigma$ we have that
\[
def(inf(\sigma))=\sigma=inf(def(\sigma)) \]

Let’s construct at least two such Conway tilings (later we’ll see that there are uncountably many). Take $C_n=def^n(LS\underline{L})$ and write it in a special form to highlight symmetries.
\begin{eqnarray*}
C_0 =& (L.S)\underline{L} \\
C_1 =& L(S.L)\underline{L}S \\
C_2 =& LSL(L.S)\underline{L}SL \\
C_3 =& LSLLSL(S.L)\underline{L}SLLS \\
C_4 =& LSLLSLSLLSL(L.S)\underline{L}SLLSLSL
\end{eqnarray*}

The even terms have middle-part $(L.S)$ and the odd ones $(S.L)$. The remaing left and right parts are each others reflexion (or part of it). This is easily seen by induction as are the inclusions
\[
C_0 \subset C_2 \subset C_4 \subset \dots \subset C_{even} \quad \text{and} \quad C_1 \subset C_3 \subset C_5 \subset \dots \subset C_{odd} \]

$C_{even}$ and $C_{odd}$ are special Conway musical sequences, called the middle $C$-sequences, and are each others inflation and deflation. If you are familiar with Penrose tilings, these are the $1$-dimensional counterparts of the cartwheel Penrose tiling (here with the $10$ Conway worms emanating from the center, and with the borders of the first few cartwheels drawn).

A direct consequence of inflation on Conway’s musical sequences is that the corresponding tiling is aperiodic, that is, it has no translation symmetry.

For, inflation only depends on the local configuration of tiles, so if translation by $R$ is a symmetry of a musical sequence $\sigma$ then it is also a symmetry of $inf(\sigma)$, and so also of $inf^n(\sigma)$. But for large $n$ we will have that $R < \tau^n a$ (with $a$ the size of the tiles in $\sigma$). But then a tile in $inf^n(\sigma)$ and its translation by $R$ must overlap which is impossible if $+R$ is a translation symmetry of $inf^n(\sigma)$. Done!

Returning to the middle C-sequences, what was the point of starting with $C_0 = LSL$? Well, it follows directly from the gluing restrictions that any letter in a musical sequence is part of a subword $LSL$ of $\sigma$. But then, every finite subword $W$ of $\sigma$ is also a subword of $C_{2n}$ for some large $n$.

For, let $d$ be the length of the interval corresponding to $W$ and choose $n$ such that $d > \tau^{2n} a$ then the interval of the line corresponding to $W$ is contained in a single tile in $inf^{2n}(\sigma)$ and this tile belongs to a subword $LSL$ of $inf^{2n}(\sigma)$. But then $W$ will be a subword of the $2n$-th deflation of that interval $LSL \subset inf^{2n}(\sigma)$, which is $C_{2n}$.

Or, as Conway would phrase it with respect to Penrose tilings (quote again from Siobhan Roberts’ book)

“Every points is in the cartwheel somewhere. If you jab your finger anywhere, on any point anywhere on teh pattern, you are part of a cartwheel. The whole ting is overlapping cartwheels.”

An immediate consequence is the local isomorphism theorem: Every subword of a musical sequence $\sigma$ appears infinitely many times as subword of any other musical sequence. That is, one cannot distinguish two tilings of the line with musical sequence codes from each other by looking at finite intervals!

The argument is similar to the one above. The finite interval corresponding to the subword lies in a unique tile of $inf^n(\sigma)$ for $n$ large enough. Now, take another musical sequence $\mu$ and consider any of the infinitely many tiles of the same type in $inf^n(\mu)$, then $def^n$ of such a tile will contain the subword in $\phi$.

Another time, we’ll see that musical sequences can be produced by the ‘cut-and-project’-method (what I called the ‘windows’-method before).
This time we will project parts of the standard $2$-dimensional lattice $\mathbb{Z}^2$ onto the line, which is a lot easier to visualise than de Bruijn’s projection from $\mathbb{R}^5$ to produce Penrose tilings or the projection from six dimensional space to harvest quasicrystals.

Leave a Comment