Take an affine $\mathbb{C} $-algebra A (not necessarily commutative). We will assign to it a strange object called the tangent-quiver $\vec{t}~A $, compute it in a few examples and later show how it connects with existing theory and how it can be used. This series of posts can be seen as the promised notes of my talks at the GAMAP-workshop but in reverse order… If some of the LaTeX-pictures are not in the desired spots, please size and resize your browser-window and they will find their intended positions.
A vertex $v $ of $\vec{t}~A $ corresponds to the isomorphism class of a finite dimensional simple A-representations $S_v $ and between any two such vertices, say $v $ and $w $, the number of directed arrows from $v $ to $w $ is given by the dimension of the Ext-space
$dim_{\mathbb{C}}~Ext^1_A(S_v,S_w) $
Recall that this Ext-space counts the equivalence classes of short exact sequences of A-representations
[tex]\xymatrix{0 \ar[r] & S_w \ar[r] & V \ar[r] & S_v \ar[r] & 0}[/tex]
where two such sequences (say with middle terms V resp. W) are equivalent if there is an A-isomorphism $V \rightarrow^{\phi} W $ making the diagram below commutative
[tex]\xymatrix{0 \ar[r] & S_w \ar[r] \ar[d]^{id_{S_w}} & V \ar[r] \ar[d]^{\phi} & S_v \ar[r] \ar[d]^{id_{S_v}} & 0 \\\
0 \ar[r] & S_w \ar[r] & W \ar[r] & S_v \ar[r] & 0}[/tex]
The Ext-space measures how many non-split extensions there are between the two simples and is always a finite dimensional vectorspace. So the tangent quiver $\vec{t}~A $ has the property that in all vertices there are at most finitely many loops and between any two vertices there are a finite number of directed arrows, but in principle a vertex may be the origin of arrows connecting it to infinitely many other vertices.
Right, now let us at least motivate the terminology. Let $X $ be a (commutative) affine variety with coordinate ring $A = \mathbb{C}[X] $ then what is $\vec{t}~A $ in this case? To begin, as $\mathbb{C}[X] $ is commutative, all its finite dimensional simple representations are one-dimensional and there is one such for every point $x \in X $. Therefore, the vertices of $\vec{t}~A $ correspond to the points of the affine variety $X $. The simple A-representation $S_x $ corresponding to a point $x $ is just evaluating polynomials in $x $. Moreover, if $x \not= y $ then there are no non-split extensions between $S_x $ and $S_y $ (a commutative semi-local algebra splits as a direct sum of locals), therefore in $\vec{t}~A $ there can only be loops and no genuine arrows between different vertices. Finally, the number of loops in the vertex corresponding to the point $x $ can be computed using the fact that the self-extensions can be identified with the tangent space at $x $, that is
$dim_{\mathbb{C}}~Ext^1_{\mathbb{C}[X]}(S_x,S_x) = dim_{\mathbb{C}}~T_x~X $
That is, if $A=\mathbb{C}[X] $ is the coordinate ring of an affine variety $X $, then the quiver $\vec{t}~A $ is the set of points of $X $ having in each point $x $ as many loops as the dimension of the tangent space $T_x~X $. So, in this case, the quiver $\vec{t}~A $ contains all information about tangent spaces to the variety and that’s why we call it the tangent quiver.
Let’s go into the noncommutative wilderness. A first, quite trivial, example is the group algebra $A = \mathbb{C} G $ of a finite group $G $, then the simple A-representations are just the irreducible G-representations and as the group algebra is semi-simple every short exact sequence splits so all Ext-spaces are zero. That is, in this case the tangent quiver $\vec{t}~A $ in just a finite set of vertices (as many as there are irreducible G-representations) and no arrows nor loops.
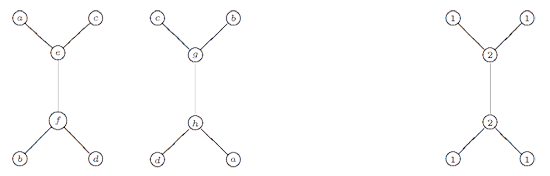
Now you may ask whether there are examples of tangent quivers having arrows apart from loops. So, take another easy finite dimensional example : the path algebra $A = \mathbb{C} Q $ of a finite quiver $Q $ without oriented cycles. Recall that the path algebra is the vectorspace having as basis all vertices and all oriented paths in the quiver Q (and as there are no cycles, this basis is finite) and multiplication is induced by concatenation of paths. Here an easy example. Suppose the quiver Q looks like
[tex]\xymatrix{\vtx{} \ar[r] & \vtx{} \ar[r] & \vtx{}}[/tex]
then the path algebra is 6 dimensional as there are 3 vertices, 2 paths of length one (the arrows) and one path of length two (going from the leftmost to the rightmost vertex). The concatenation rule shows that the three vertices will give three idempotents in A and one easily verifies that the path algebra can be identified with upper-triangular $3 \times 3 $ matrices
$\mathbb{C} Q \simeq \begin{bmatrix} \mathbb{C} & \mathbb{C} & \mathbb{C} \\\ 0 & \mathbb{C} & \mathbb{C} \\\ 0 & 0 & \mathbb{C} \end{bmatrix} $
where the diagonal components correspond to the vertices, the first offdiagonal components to the two arrows and the corner component corresponds to the unique path of length two. Right, for a general finite quiver without oriented cycles is the quite easy to see that all finite dimensional simples are one-dimensional and correspond to the vertex-idempotents, that is every simple is of the form $S_v = e_v \mathbb{C} Q e_v $ where $e_v $ is the vertex idempotent. No doubt, you can guess what the tangent quiver $\vec{t}~A = \vec{t}~\mathbb{C} Q $ will be, can’t you?
5 Comments Here, the vertex spaces on the left are the iso-typical factors of $V \downarrow_{D_2} $ and those on the right those of $V \downarrow_{D_3} $ and the arrows give the block-components of the $C_2 $-isomorphism $\phi $. The nice things is that one can also reverse this process to get all $\tilde{\Gamma} $-representations from $\theta $-semistable representations of this quiver (having the additional condition that the square matrix made of the arrows is invertible) and isomorphisms of group-representation correspond to those of quiver-representations!
Here, the vertex spaces on the left are the iso-typical factors of $V \downarrow_{D_2} $ and those on the right those of $V \downarrow_{D_3} $ and the arrows give the block-components of the $C_2 $-isomorphism $\phi $. The nice things is that one can also reverse this process to get all $\tilde{\Gamma} $-representations from $\theta $-semistable representations of this quiver (having the additional condition that the square matrix made of the arrows is invertible) and isomorphisms of group-representation correspond to those of quiver-representations!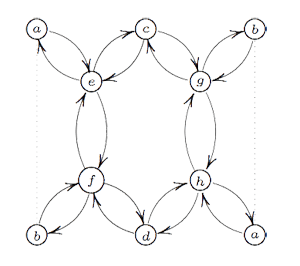 If one calculates the ‘clan’ of these 8 simples one obtains the double quiver of the graph on the left. Note that a and b appear twice, so one should glue the left and right hand sides together as a Moebius-strip. That is, the clan determining the representation theory of the extended modular group is a Moebius strip made of two hexagons!
If one calculates the ‘clan’ of these 8 simples one obtains the double quiver of the graph on the left. Note that a and b appear twice, so one should glue the left and right hand sides together as a Moebius-strip. That is, the clan determining the representation theory of the extended modular group is a Moebius strip made of two hexagons!