Siegel – neverendingbooks

SNORT, invented by Simon NORTon is a map-coloring game, similar to COL. Only, this time, neighbours may not be coloured differently.

SNORTgo, similar to COLgo, is SNORT played with go-stones on a go-board. That is, adjacent stones must have the same colour.

SNORT is a ‘hot’ game, meaning that each player is eager to move as most moves will improve your position. In COL players are reluctant to move, because a move limits your next moves.

For this reason, SNORT positions are much harder to evaluate, and one needs the full force of Conways’s ONAG.

Here’s a SNORTgo endgame. Who has a winning strategy?, and what is the first move in that strategy?

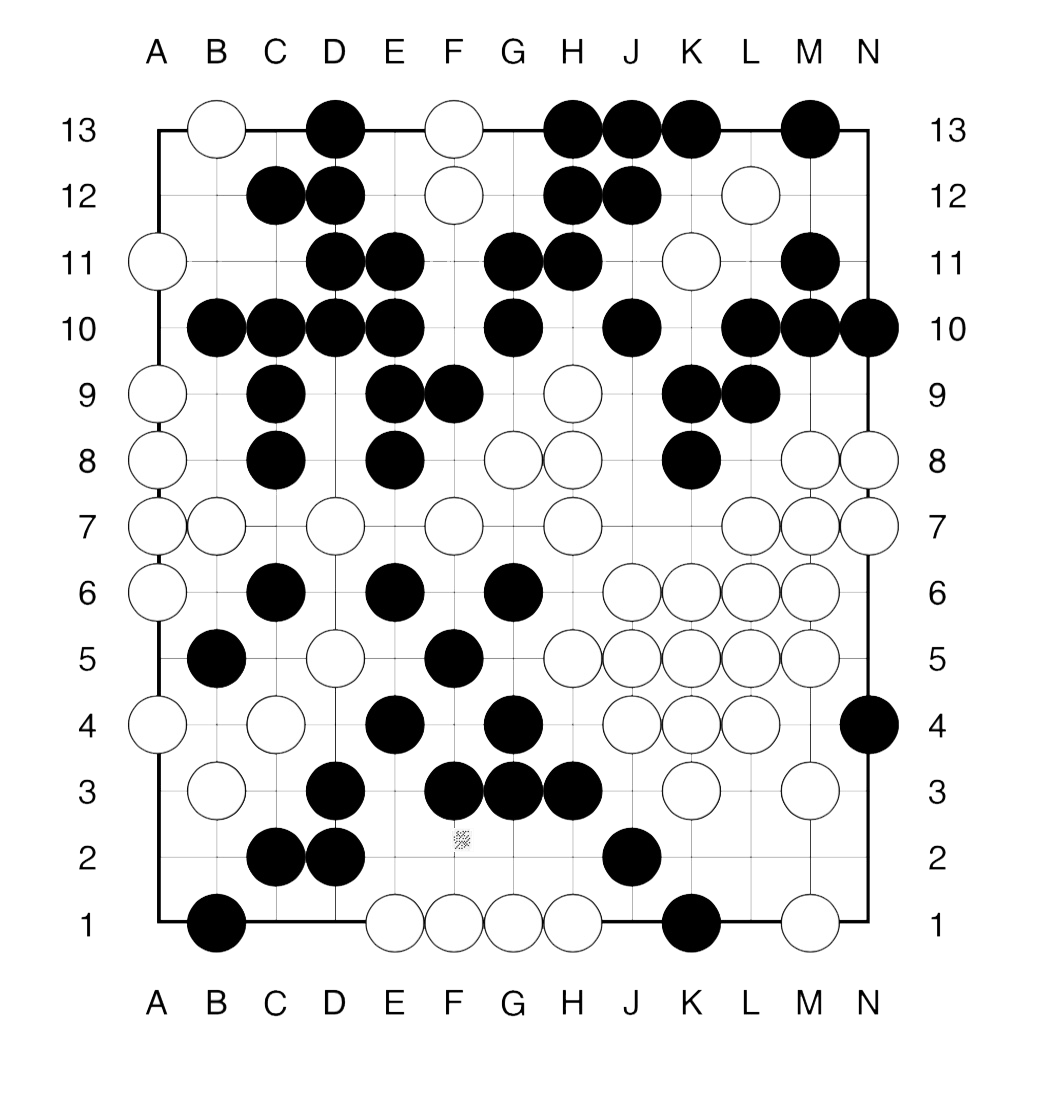
The method to approach such an endgame is similar to that in COLgo. First we remove all dead spots from the board.

What remains, are a 4 spots available only to Right (white) and 5 spots available only to Left (bLack). Further, there a 3 ‘live’ regions: the upper righthand corner and the two lower corners.

The value of these corners must be computed inductively.

Here’s the answer:

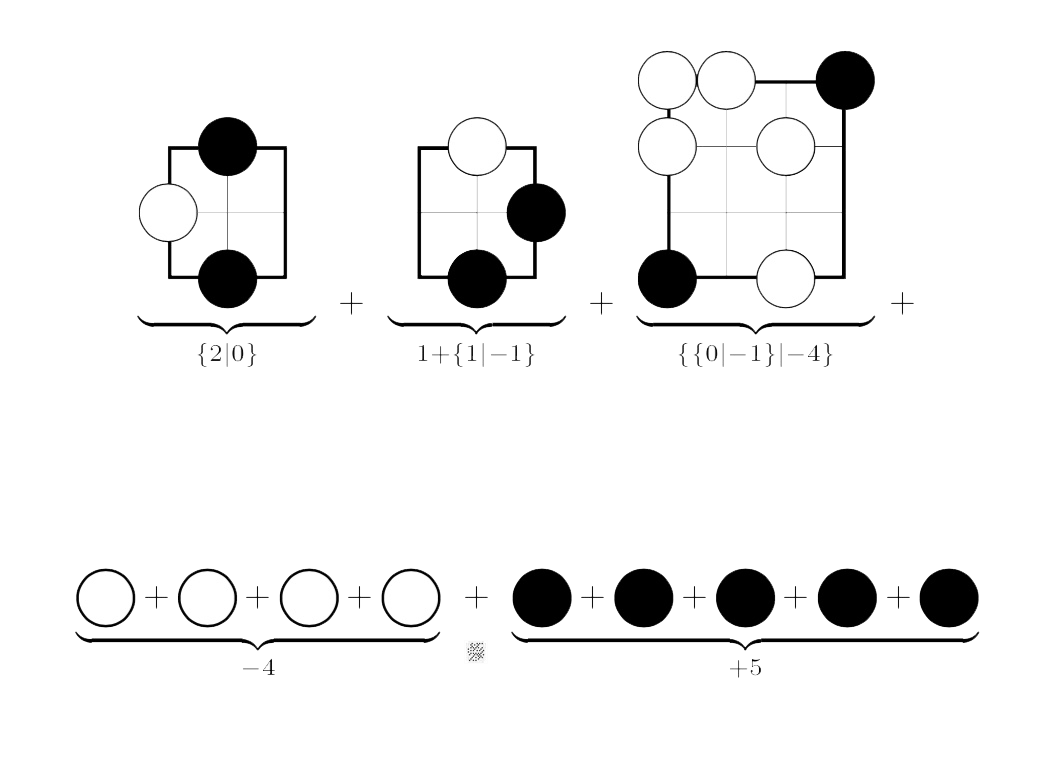
For example, Right’s best option in the left-most game (corresponding to the upper righthand corner of the endgame) is to put his stone on N12, resulting in a game in which neither player can move (the zero game).

On the other hand, Left can put a stone at either N11, N12 or N13 leaving a game in which she has two more moves, whereas Right han none (the $2$ game).

The other positions are computed similarly.

To get the value of the endgame we have to sum up all these values.

This can either be done using the addition rule given in ONAG, or by using programs in combinatorial game theory.

There’s Combinatorial Game Suite, developed by Aaron Siegel. But, for some reason I can no longer use it on macOS High Sierra.

Fortunately, the older program David Wolfe’s toolkit is still available, and runs on my MacBook.

The sum game evaluates to $\{ \{3|2 \}|-1 \}$, which is a ‘fuzzy’ game, that is, its value is confused with $0$.

This means that the first player to move has a winning strategy in the endgame.

Can you spot the (unique) winning move for Right (white) and one (of two) winning move for Left (bLack)?

Spoiler alert : solution in the comments.

One Comment

One of the coolest (pure math) facts in Conway’s book ONAG is the explicit construction of the algebraic closure $\overline{\mathbb{F}_2}$ of the field with two elements as the set of all ordinal numbers smaller than $(\omega^{\omega})^{\omega}$ equipped with nimber addition and multiplication.

Some time ago we did run a couple of posts on this. In transfinite number hacking we recalled Cantor’s ordinal arithmetic and in Conway’s nim arithmetics we showed that Conway’s simplicity rules for addition and multiplication turns the set of all ordinal numbers into a field of characteristic zero : $\mathbb{On}_2$ (pronounced ‘Onto’).

In the post extending Lenstra’s list we gave Hendrik Lenstra’s effective construction of the mystery elements $\alpha_p$ (for prime numbers $p$) needed to do actual calculations in $\mathbb{On}_2$. We used SAGE to check the values for $p \leq 41$ and solved the conjecture left in Lenstra’s paper Nim multiplication that $(\omega^{\omega^{13}})^{43} = \omega^{\omega^7} + 1$ and determined $\alpha_p$ for $p \leq 67$.

Aaron Siegel has now dramatically extended this and calculated the $\alpha_p$ for all primes $p \leq 181$. He mails :

“thinking about the problem I figured it shouldn’t be too hard to write a dedicated program for it. So I threw together some Java code and… pushed the table up to p = 181! You can see the results below. Q(f(p)), excess, and alpha_p are all as defined by Lenstra. The “t(sec)” column is the number of seconds the calculation took, on my 3.4GHz iMac. The most difficult case, by far, was p = 167, which took about five days.

I’m including results for all p < 300, except for p = 191, 229, 263, and 283. p = 263 and 283 are omitted because they involve computations in truly enormous finite fields (exponent 102180 for p = 263, and 237820 for p = 283). I'm confident that if I let my computer grind away at them for long enough, we'd get an answer... but it would take several months of CPU time at least. p = 191 and 229 are more troubling cases. Consider p = 191: it's the first prime p such that p-1 has a factor with excess > 1. (190 = 2 x 5 x 19, and alpha_19 has excess 4.) This seems to have a significant effect on the excess of alpha_191. I’ve tried it for every excess up to m = 274, and for all powers of 2 up to m = 2^32. No luck.”

Aaron is writing a book on combinatorial game theory (to be published in the AMS GSM series, hopefully later this year) and will include details of these computations. For the impatient, here’s his list

Tag: Siegel

a SNORTgo endgame

Aaron Siegel on transfinite number hacking