Skip to content →

Tag: permutation representation

Iguanodon series of simple groups

Published November 7, 2007 by lievenlb

Bruce Westbury has a page on recent work on series of Lie groups including exceptional groups. Moreover, he did put his slides of a recent talk (probably at MPI) online.

Probably, someone considered a similar problem for simple groups. Are there natural constructions leading to a series of finite simple groups including some sporadic groups as special members ? In particular, does the following sequence appear somewhere ?

$L_2(7), M_{12}, A_{16}, M_{24}, A_{28}, A_{40}, A_{48}, A_{60}, \ldots $

Here, $L_2(7) $ is the simple group of order 168 (the automorphism group of the Klein quartic), $M_{12} $ and $M_{24} $ are the sporadic Mathieu groups and the $A_n $ are the alternating simple groups.

I’ve stumbled upon this series playing around with Farey sequences and their associated ‘dessins d’enfants’ (I’ll come back to the details of the construction another time) and have dubbed this sequence the Iguanodon series because the shape of the doodle leading to its first few terms

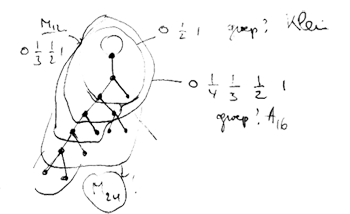
reminded me of the Iguanodons of Bernissart (btw. this sketch outlines the construction to the experts). Conjecturally, all groups appearing in this sequence are simple and probably all of them (except for the first few) will be alternating.

I did verify that none of the known low-dimensional permutation representations of other sporadic groups appear in the series. However, there are plenty of similar sequences one can construct from the Farey sequences, and it would be nice if one of them would contain the Conway group $Co_1 $. (to be continued)

4 Comments

Hyperbolic Mathieu polygons

Published June 27, 2007 by lievenlb

Today we will link modular quilts (via their associated cuboid tree diagrams) to special hyperbolic polygons. The above drawing gives the hyperbolic polygon (the gray boundary) associated to the M(24) tree diagram (the black interior graph). In general, the correspondence goes as follows.

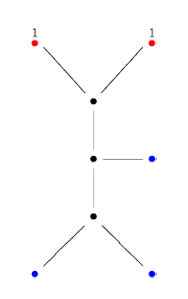
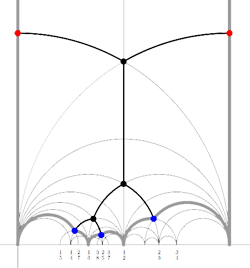
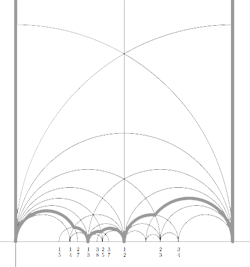
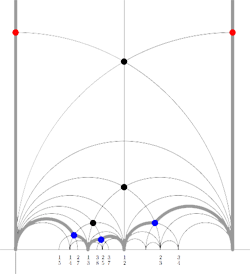
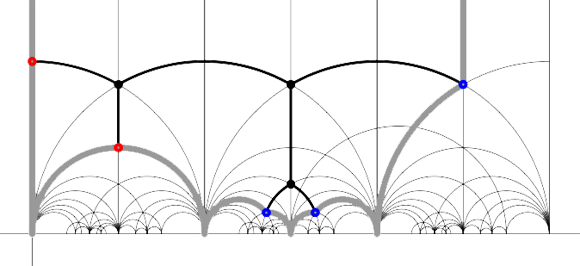
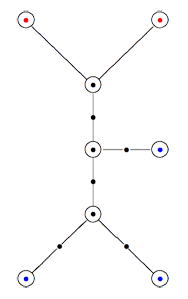Recall that a cuboid tree diagram is a tree such that all internal vertices are 3-valent and have a specified ordering on the incident edges (given by walking counterclockwise around the vertex) and such that all leaf-vertices are tinted blue or red, the latter ones are paired via an involution (indicated by giving paired red vertices the same label). Introduce a new 2-valent vertex on all edges joining two internal vertices or a blue vertex to an internal vertex. So, the picture on the right corresponds to the tree diagram on the left. 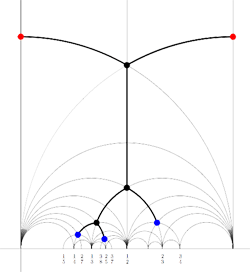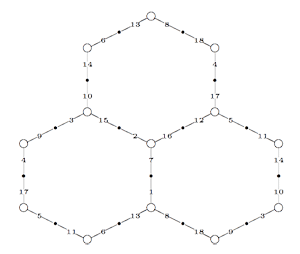Equip this extended tree with a metric such that every edge has length equal to an f-edge in the Dedekind tessellation. Fix an edge having a red vertex and develop this isometrically onto the f-edge connecting $i $ to $\rho $ in the tessellation. Then, the extended tree develops uniquely along the f-edges of the tessellation and such that the circled black and blue vertices correspond to odd vertices, the circled red and added uncircled vertices correspond to even vertices in the tessellation. Starting from the above tree (and choosing the upper-left edge to start the embedding), we obtain the picture on the left (we have removed the added 2-valent vertices)

We will now associate a special hyperbolic polygon to this tree. At a red vertex take the even line going through the vertex. If under the involution the red vertex is send to itself, the even edges will be paired. Otherwise, the line is a free side and will be paired to the free side containing the red vertex corresponding under the involution. At a blue vertex, take the two odd edges making an angle of $\frac{\pi}{3} $ with the tree-edge containing the blue vertex. These odd edges will be paired. If we do this procedure for all blue and red vertices, we obtain a special polygon (see the picture on the right, the two vertical lines are paired).
Conversely, suppose we start with a special polygon such as the one on the left below

and consider all even and odd vertices on the boundary (which are tinted red, respectively blue) together with all odd vertices in the interior of the special polygon. These are indicated in the picture on the right above. If we connect these vertices with the geodesics in the polygon we get a cuboid tree diagram. This correspondence special polygons —>> tree diagrams is finite to one as we have made a choice in the starting red vertex and edge. If we would have taken the other edge containing a red vertex we would end up with the following special polygon

It is no accident that these two special polygons consist of exactly 24 triangles of the Dedekind tessellation as they correspond to the index 12 subgroup of the modular group $\Gamma $ determining the 12-dimensional permutation representation of the Mathieu group $M_{12} $. Similarly, the top drawing has 48 hyperbolic triangles and corresponds to the 24-dimensional permutation representation of $M_{24} $. Another time we will make the connection with Farey series which will allow us to give free generators of finite index subgroups.

Reference

Ravi S. Kulkarni, “An arithmetic-geometric method in the study of the subgroups of the modular group”, Amer. J. Math. 113 (1991) 1053-1133

Continue readingHyperbolic Mathieu polygons
One Comment

Modular quilts and cuboid tree diagrams

Published June 25, 2007 by lievenlb

Conjugacy classes of finite index subgroups of the modular group $\Gamma = PSL_2(\mathbb{Z}) $ are determined by a combinatorial gadget : a modular quilt. By this we mean a finite connected graph drawn on a Riemann surface such that its vertices are either black or white. Moreover, every edge in the graph connects a black to a white vertex and the valency (that is, the number of edges incodent to a vertex) of a black vertex is either 1 or 2, that of a white vertex is either 1 or 3. Finally, for every white vertex of valency 3, there is a prescribed cyclic order on the edges incident to it.

On the left a modular quilt consisting of 18 numbered edges (some vertices and edges re-appear) which gives a honeycomb tiling on a torus. All white vertices have valency 3 and the order of the edges is given by walking around a point in counterclockwise direction. For example, the order of the edges at the top left vertex (which re-appears at the middle right vertex) can be represented by the 3-cycle (6,11,14), that around the central vertex gives the 3-cycle (2,7,16).

Continue readingModular quilts and cuboid tree diagrams
4 Comments