Tag: nonsense

Scottish solids, final(?) comments

Published June 5, 2012 by lievenlb

In the spring of 2009 I did spend a fortnight dog-sitting in a huge house in the countryside, belonging to my parents-in-law, who both passed away the year before.

That particular day it was raining and thundering heavily. To distract myself from the sombre and spooky atmosphere in the house I began to surf the web looking for material for a new series of blogposts (yes, in those days I was still thinking in ‘series’ of posts…).

Bookmarks for that day tell me that the first picture grasping my attention was Salvador Dali’s Sacrament of the last supper, in particular the depicted partial dodecahedron

I did compare it with Leonardo’s last supper and in the process stumbled upon Leonardo’s drawings of polyhedra, among which these two dodecahedra

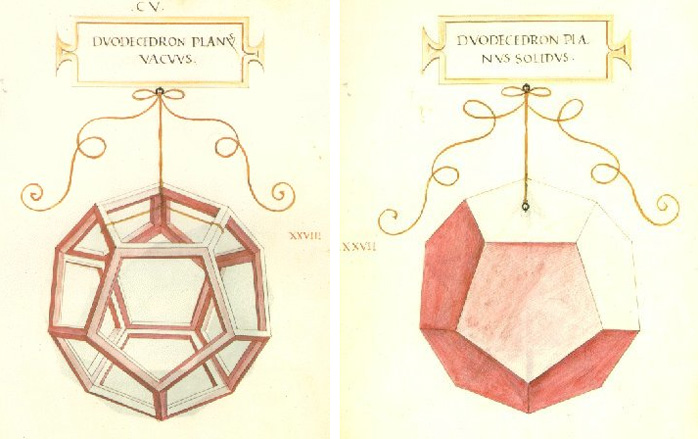
From there it went on and on : the Mystery of the 2nd and 3rd Century Roman Dodecahedron and its posible use ‘casting dodecahedra’ in Tarot Divination Without Tarot Cards or as an astronomical instrument, a text on polyhedra and plagiarism in the renaissance, the history of the truncated icosahedron, a Bosnian pyramid and its stone balls, the sacred geometry of the dodecahedron, mathematics in the Vatican library, and on and on and on…

By noon, I felt I had enough material to post for a couple of weeks on “platonic solids through the ages”.

In between two rain showers, I walked the dog, had a quick lunch, and started writing.

I wanted to approach the topic in chronological order, and as I had done already a quicky on Scottish solids, the first post of the series would have to extend on this picture of five stone balls from the Ashmolean museum (or so it was claimed).

So, I hunted for extra pictures of these stone balls from the Ashmolean, and when comparing the two, clearly something had to be wrong…

It took me a couple of hours to catch up with the scientific literature on these Scottish balls, their cataloguing system and the museums of Scotland and England that house them.

Around 4pm I had compiled a list of all potential dodecahedra and icosahedra Scottish balls: ‘there are only 8 possible candidates for a Scottish dodecahedron (below their catalogue numbers, indicating to the knowledgeable which museum owns them and where they were found)

NMA AS 103 : Aberdeenshire
AS 109 : Aberdeenshire
AS 116 : Aberdeenshire (prob)
AUM 159/9 : Lambhill Farm, Fyvie, Aberdeenshire
Dundee : Dyce, Aberdeenshire
GAGM 55.96 : Aberdeenshire
Montrose = Cast NMA AS 26 : Freelands, Glasterlaw, Angus
Peterhead : Aberdeenshire

The case for a Scottish icosahedron looks even worse. Only two balls have exactly 20 knobs

NMA AS 110 : Aberdeenshire
GAGM 92 106.1. : Countesswells, Aberdeenshire’

About an hour later I’d written the post, clicked the ‘Publish’ button and The Scottish solids hoax, began to live a life of its own!

From the numerous reactions let me single out 3 follow-ups which I believe to be most important.

John McKay and Tom Leinster did some legwork, tracking down resp. photographer and one of the 20 knobs balls.

John Baez gave a talk at an AMS meeting dedicated to the history of mathematics on Who discovered the icosahedron? mentioning my post and extending it by:

“And here is where I did a little research of my own. The library at UC Riverside has a copy of Keith Critchlow’s 1979 book Time Stands Still. In this book, we see the same photo of stones with ribbons that appears in Lawlor’s book – the photo that Atiyah and Suttcliffe use. In Critchlow’s book, these stones are called “a full set of Neolithic ‘Platonic solids'”. He says they were photographed by one Graham Challifour – but he gives no information as to where they came from!

And Critchlow explicitly denies that the Ashmolean has an icosahedral stone! He writes:

… the author has, during the day, handled five of these remarkable objects in the Ashmolean museum…. I was rapt in admiration as I turned over these remarkable stone objects when another was handed to me which I took to be an icosahedron…. On careful scrutiny, after establishing apparent fivefold symmetry on a number of the axes, a count-up of the projections revealed 14! So it was not an icosahedron.”

And now there is even a published paper out!

Bob Lloyd wrote How old are the Platonic solids?, published in BSHM Bulletin: Journal of the British Society for the History of Mathematics. The full article is behind a paywall but Bob graciously send me a copy.

Bob believes the balls in the picture to belong to the Scottish ‘National Museum of Antiquities’ (NMA in the Marshall list), now the National Museum of Scotland (NMS) in Edinburgh.

He believes the third and fourth ball to be two pictures of the same object “recorded as having been discovered in Aberdeenshire” so it should be NMA AS 103 : Aberdeenshire in the above list. (Or, the other one may be NMA AS 26?).

He also attempts to identify the other 3 balls with objects in the NMS-collection. In short, he gives compelling evidence that the picture must have been taking in Edinburg and exists of genuine artifacts.

Perhaps even more important is that he finally puts the case of a Scottish icosahedron to rest. As mentioned above, there are just two candidates NMA AS 110 (Edinburg) and GAGM 92 106.1 (Glasgow). He writes:

“According to the Marshall list, there are only two balls known which have 20K; one of these is at the NMS. Alan Saville, Senior Curator for Earliest Prehistory at this Museum, has provided a photograph which shows that this object is complex, and certainly not a dodecahedron. It could be considered as a modified octahedron, with five large knobs in the usual positions, but with the sixth octahedral position occupied by twelve small knobs, and in addition there are also three small triangles carved at some of the interstices, the three-fold positions of the ‘octahedron’. These make up a total of twenty ‘protrusions’, though the word ‘knobs’ is hard to justify.

The other 20K object is at the Kelvingrove museum in Glasgow. Photographs taken by Tracey Hawkins, assistant curator, show that this also is very far from being a dodecahedron, though this time there are twenty clearly defined knobs of roughly the same size. The shape is somewhat irregular, but two six-sided pyramids can be picked out, and much of the structure, though not all, is deltahedral in form, with sets of three balls at the corners of equilateral triangles.”

So, sadly for John McKay, there is no Scottish icosahedron out there!

One final comment. Both John Baez (in a comment) and Bob Lloyd (in a comment and in his paper) argue that I shouldn’t have used the term “hoax” for something that is merely a ‘matter of sloppy scholarship’.

My apologies.

Given Bob’s evidence that the balls in the picture are genuine artifacts, I have deleted the ‘fabrication or falsification’-phrase in the original post.

Summarizing : the Challifour photograph is not taken at the Ashmolean museum, but at the National Museum of Scotland in Edinburgh and consists of 5 of their artifacts (or 4 if ball 3 and 4 are identical) vaguely resembling cube, tetrahedron, dodecahedron (twice) and octahedron. The fifth Platonic solid, the icosahedron, remains elusive.

Art and the absolute point (3)

Published May 19, 2011 by lievenlb

Previously, we have recalled comparisons between approaches to define a geometry over the absolute point and art-historical movements, first those due to Yuri I. Manin, subsequently some extra ones due to Javier Lopez Pena and Oliver Lorscheid.

In these comparisons, the art trend appears to have been chosen more to illustrate a key feature of the approach or an appreciation of its importance, rather than giving a visual illustration of the varieties over $\mathbb{F}_1$ the approach proposes.

Some time ago, we’ve had a couple of posts trying to depict noncommutative varieties, first the illustrations used by Shahn Majid and Matilde Marcolli, and next my own mental picture of it.

In this post, we’ll try to do something similar for affine varieties over the absolute point. To simplify things drastically, I’ll divide the islands in the Lopez Pena-Lorscheid map of $\mathbb{F}_1$ land in two subsets : the former approaches (all but the $\Lambda$-schemes) and the current approach (the $\Lambda$-scheme approach due to James Borger).

The former approaches : Francis Bacon “The Pope” (1953)

The general consensus here was that in going from $\mathbb{Z}$ to $\mathbb{F}_1$ one looses the additive structure and retains only the multiplicative one. Hence, ‘commutative algebras’ over $\mathbb{F}_1$ are (commutative) monoids, and mimicking Grothendieck’s functor of points approach to algebraic geometry, a scheme over $\mathbb{F}_1$ would then correspond to a functor

$h_Z~:~\mathbf{monoids} \longrightarrow \mathbf{sets}$

Such functors are described largely by combinatorial data (see for example the recent blueprint-paper by Oliver Lorscheid), and, if the story would stop here, any Rothko painting could be used as illustration.

Most of the former approaches add something though (buzzwords include ‘Arakelov’, ‘completion at $\infty$’, ‘real place’ etc.) in order to connect the virtual geometric object over $\mathbb{F}_1$ with existing real, complex or integral schemes. For example, one can make the virtual object visible via an evaluation map $h_Z \rightarrow h_X$ which is a natural transformation, where $X$ is a complex variety with its usual functor of points $h_X$ and to connect both we associate to a monoid $M$ its complex monoid-algebra $\mathbb{C} M$. An integral scheme $Y$ can then be said to be ‘defined over $\mathbb{F}_1$’, if $h_Z$ becomes a subfunctor of its usual functor of points $h_Y$ (again, assigning to a monoid its integral monoid algebra $\mathbb{Z} M$) and $Y$ is the ‘best’ integral scheme approximation of the complex evaluation map.

To illustrate this, consider the painting Study after Velázquez’s Portrait of Pope Innocent X by Francis Bacon (right-hand painting above) which is a distorded version of the left-hand painting Portrait of Innocent X by Diego Velázquez.

Here, Velázquez’ painting plays the role of the complex variety which makes the combinatorial gadget $h_Z$ visible, and, Bacon’s painting depicts the integral scheme, build up from this combinatorial data, which approximates the evaluation map best.

All of the former approaches more or less give the same very small list of integral schemes defined over $\mathbb{F}_1$, none of them motivically interesting.

The current approach : Jackson Pollock “No. 8” (1949)

An entirely different approach was proposed by James Borger in $\Lambda$-rings and the field with one element. He proposes another definition for commutative $\mathbb{F}_1$-algebras, namely $\lambda$-rings (in the sense of Grothendieck’s Riemann-Roch) and he argues that the $\lambda$-ring structure (which amounts in the sensible cases to a family of endomorphisms of the integral ring lifting the Frobenius morphisms) can be viewed as descent data from $\mathbb{Z}$ to $\mathbb{F}_1$.

The list of integral schemes of finite type with a $\lambda$-structure coincides roughly with the list of integral schemes defined over $\mathbb{F}_1$ in the other approaches, but Borger’s theory really shines in that it proposes long sought for mystery-objects such as $\mathbf{spec}(\mathbb{Z}) \times_{\mathbf{spec}(\mathbb{F}_1)} \mathbf{spec}(\mathbb{Z})$. If one accepts Borger’s premise, then this object should be the geometric object corresponding to the Witt-ring $W(\mathbb{Z})$. Recall that the role of Witt-rings in $\mathbb{F}_1$-geometry was anticipated by Manin in Cyclotomy and analytic geometry over $\mathbb{F}_1$.

But, Witt-rings and their associated Witt-spaces are huge objects, so one needs to extend arithmetic geometry drastically to include such ‘integral schemes of infinite type’. Borger has made a couple of steps in this direction in The basic geometry of Witt vectors, II: Spaces.

To depict these new infinite dimensional geometric objects I’ve chosen for Jackson Pollock‘s painting No. 8. It is no coincidence that Pollock-paintings also appeared in the depiction of noncommutative spaces. In fact, Matilde Marcolli has made the connection between $\lambda$-rings and noncommutative geometry in Cyclotomy and endomotives by showing that the Bost-Connes endomotives are universal for $\lambda$-rings.

One Comment

Who dreamed up the primes=knots analogy?

Published May 16, 2011 by lievenlb

One of the more surprising analogies around is that prime numbers can be viewed as knots in the 3-sphere $S^3$. The motivation behind it is that the (etale) fundamental group of $\pmb{spec}(\mathbb{Z}/(p))$ is equal to (the completion) of the fundamental group of a circle $S^1$ and that the embedding

$\pmb{spec}(\mathbb{Z}/(p)) \subset \pmb{spec}(\mathbb{Z})$

embeds this circle as a knot in a 3-dimensional simply connected manifold which, after Perelman, has to be $S^3$. For more see the what is the knot associated to a prime?-post.

In recent months new evidence has come to light allowing us to settle the genesis of this marvelous idea.

1. The former consensus

Until now, the generally accepted view (see for example the ‘Mazur-dictionary-post’ or Morishita’s expository paper) was that the analogy between knots and primes was first pointed out by Barry Mazur in the middle of the 1960’s when preparing for his lectures at the Summer Conference on Algebraic Geometry, at Bowdoin, in 1966. The lecture notes where later published in 1973 in the Annales of the ENS as ‘Notes on etale cohomology of number fields’.

For further use in this series of posts, please note the acknowledgement at the bottom of the first page, reproduced below : “It gives me pleasure to thank J.-P. Serre for his vigorous editing and his suggestions and corrections, which led to this revised version.”

Independently, Yuri I. Manin spotted the same analogy at around the same time. However, this point of view was quickly forgotten in favor of the more classical one of viewing number fields as analogous to algebraic function fields of one variable. Subsequently, in the mid 1990’s Mikhail Kapranov and Alexander Reznikov took up the analogy between number fields and 3-manifolds again, and called the resulting study arithmetic topology.

2. The new evidence

On december 13th 2010, David Feldman posted a MathOverflow-question Mazur’s unpublished manuscript on primes and knots?. He wrote : “The story of the analogy between knots and primes, which now has a literature, started with an unpublished note by Barry Mazur. I’m not absolutely sure this is the one I mean, but in his paper, Analogies between group actions on 3-manifolds and number fields, Adam Sikora cites B. Mazur, Remarks on the Alexander polynomial, unpublished notes.“

Two months later, on february 15th David Feldman suddenly found the missing preprint in his mail-box and made it available. The preprint is now also available from Barry Mazur’s website. Mazur adds the following comment :

“In 1963 or 1964 I wrote an article Remarks on the Alexander Polynomial [PDF] about the analogy between knots in the three-dimensional sphere and prime numbers (and, correspondingly, the relationship between the Alexander polynomial and Iwasawa Theory). I distributed some copies of my article but never published it, and I misplaced my own copy. In subsequent years I have had many requests for my article and would often try to search through my files to find it, but never did. A few weeks ago Minh-Tri Do asked me for my article, and when I said I had none, he very kindly went on the web and magically found a scanned copy of it. I’m extremely grateful to Minh-Tri Do for his efforts (and many thanks, too, to David Feldman who provided the lead).”

The opening paragraph of this unpublished preprint contains a major surprise!

Mazur points to David Mumford as the originator of the ‘primes-are-knots’ idea : “Mumford has suggested a most elegant model as a geometric interpretation of the above situation : $\pmb{spec}(\mathbb{Z}/p\mathbb{Z})$ is like a one-dimensional knot in $\pmb{spec}(\mathbb{Z})$ which is like a simply connected three-manifold.”

In a later post we will show that one can even pinpoint the time and place when and where this analogy was first dreamed-up to within a few days and a couple of miles.

For the impatient among you, have a sneak preview of the cradle of birth of the primes=knots idea…

Seriously now, where was the Bourbaki wedding?

Published November 25, 2009 by lievenlb

A few days before Halloween, Norbert Dufourcq (who died december 17th 1990…), sent me a comment, containing lots of useful information, hinting I did get it wrong about the church of the Bourbali wedding in the previous post.

Norbert Dufourcq, an organist and student of Andre Machall, the organist-in-charge at the Saint-Germain-des-Prés church in 1939, the place where I speculated the Bourbaki wedding took place, concluded his comment with :

“P.S. Lieven, you _do_ know about the Schola Cantorum, now, don’t you?!?”.

Euh… actually … no, I did not …

La Schola Cantorum is a private music school in Paris. It was founded in 1894 by Charles Bordes, Alexandre Guilmant and Vincent d’Indy as a counterbalance to the Paris Conservatoire’s emphasis on opera. Its alumni include many significant figures in 20th century music, such as Erik Satie and Cole Porter.

Schola Cantorum is situated 69, rue Saint Jacques, Paris, just around the corner of the Ecole Normal Superieure, home base to the Bourbakis. In fact, closer investigation reveals striking similarities and very close connections between the circle of artists at la Schola and the Bourbaki group.

In december 1934, the exact month the Bourbaki group was formed, a radical reorganisation took place at the Schola, when Nestor Lejeune became the new director. He invited several young musicians, many from the famous Dukas-class, to take up teaching positions at the Schola.

Here’s a picture of part of the Dukas class of 1929, several of its members will play a role in the upcoming events :
from left to right next to the piano : Pierre Maillard-Verger, Elsa Barraine, Yvonne Desportes, Tony Aubin, Pierre Revel, Georges Favre, Paul Dukas, René Duclos, Georges Hugon, Maurice Duruflé. Seated on the right : Claude Arrieu, Olivier Messiaen.

The mid-1930s in Paris saw the emergence of two closely-related groups with a membership which overlapped : La Spirale and La Jeune France. La Spirale was founded in 1935 under the leadership of Georges Migot; its other committee members were Paul Le Flem, his pupil André Jolivet, Edouard Sciortino, Claire Delbos, her husband Olivier Messiaen, Daniel-Lesur and Jules Le Febvre. The common link between almost all of these musicians was their connection with the Schola Cantorum.

On the left : Les Jeunes Musiciens Français : André Jolivet on the Piano. Standing from left to right :
Olivier Messiaen, Yves Baudrier, Daniel-Lesur.

Nigel Simeone wrote this about Messiaen and La Jeune France :
“The extremely original and independent-minded Messiaen had already shown himself to be a rather unexpected enthusiast for joining groups: in December 1932 he wrote to his friend Claude Arrieu about a letter from another musician, Jacques Porte, outlining plans for a new society to be called Les Jeunes Musiciens Français.
Messiaen agreed to become its vice-president, but nothing seems to have come of the project. Six months later, in June 1933, he had a frustrating meeting with Roger Désormière on behalf of the composers he described to Arrieu as ‘les quatre’, all of them Dukas pupils: Elsa Barraine, the recently-deceased Jean Cartan, Arrieu and Messiaen himself; during the early 1930s Messiaen and Arrieu organised concerts featuring all four composers.”

Finally, we’re getting a connection with the Bourbaki group! Norbert Dufourcq mentioned it already in his comment “Messiaen was also a good friend of Jean Cartan (himself a composer, and Henri’s brother)”. Henri Cartan was one of the first Bourbakis and an excellent piano player himself.

The Cartan family picture on the right : standing from left to right, father Elie Cartan (one of the few older French mathematicians respected by the Bourbakis), Henri and his mother Marie-Louise. Seated, the younger children, from left to right : Louis, Helene (who later became a mathematician, herself) and the composer Jean Cartan, who sadly died very young from tuberculoses in 1932…

The december 1934 revolution in French music at the Schola Cantorum, instigated by Messiaen and followers, was the culmination of a process that started a few years before when Jean Cartan was among the circle of revolutionados. Because Messiaen was a fiend of the Cartan family, they surely must have been aware of the events at the Schola (or because it was merely a block away from the ENS), and, the musicians’ revolt may very well have been an example to follow for the first Bourbakis…(?!)

Anyway, we now know the intended meaning of the line “with lemmas sung by the Scholia Cartanorum” on the wedding-invitation. Cartanorum is NOT (as I claimed last time) bad Latin for ‘Cartesiorum’, leading to Descartes and the Saint-Germain-des-Pres church, but is in fact passable Latin (plur. gen.) of CARTAN(us), whence the translation “with lemmas sung by the school of the Cartans”. There’s possibly a double pun intended here : first, a reference to (father) Cartan’s lemma and, of course, to La Schola where the musical Cartan-family felt at home.

Fine, but does this brings us any closer to the intended place of the Bourbaki-Petard wedding? Well, let’s reconsider the hidden ‘clues’ we discovered last time : the phrase “They will receive the trivial isomorphism from P. Adic, of the Order of the Diophantines” might suggest that the church belongs to a a religious order and is perhaps an abbey- or convent-church and the phrase “the organ will be played by Monsieur Modulo” requires us to identify this mysterious Mister Modulo, because Norbert Dufourcq rightfully observed :

“note however that in 1939, it wasn’t as common to have a friend-organist perform at a wedding as it is today: the appointed organists, especially at prestigious Paris positions, were much less likely to accept someone play in their stead.”

The history of La Schola Cantorum reveals something that might have amused Frank Smithies (remember he was one of the wedding-invitation-composers) : the Schola is located in the Convent(!) of the Brittish Benedictines…

In 1640 some Benedictine monks, on the run after the religious schism in Britain, found safety in Paris under the protection of Cardinal Richelieu and Anne of Austria at Val-de-Grace, where the Schola is now housed.

As is the case with most convents, the convent of the Brittish Benedictines did have its own convent church, now called l’église royale Notre-Dame du Val-de-Grâce (remember that one of the possible interpretations for “of the universal variety” was that the name of the church would be “Notre-Dame”…).

This church is presently used as the concert hall of La Schola and is famous for its … musical organ : “In 1853, Aristide Cavaillé-Coll installed a new organ in the Church of Sainte-geneviève which had been restored in its rôle as a place of worship by Prince President Louis-Napoléon. In 1885, upon the decision of President Jules Grévy, this church once again became the Pantheon and, six years later, according to an understanding between the War and Public Works Departments, the organ was transferred to the Val-de-Grâce, under the supervision of the organ builder Merklin. Beforehand, the last time it was heard in the Pantheon must have been for the funeral service of Victor Hugo.
In 1927, a raising was carried out by the builder Paul-Marie Koenig, and the inaugural concert was given by André Marchal and Achille Philippe, the church’s organist. Added to the register of historic monument in 1979, Val-de-Grâce’s “ little great organ ”, as Cavaillé-Coll called it, was restored in 1993 by the organ builders François Delangue and Bernard Hurvy.
The organ of Val-de-Grâce is one the rare parisian surviving witnesses of the art of Aristide Cavaillé-Coll, an instrument that escaped abusive and definitive transformations or modernizations. This explain why, in spite of its relatively modest scale, this organ enjoys quite a reputation, and this, as far as the United States.”

By why would the Val-de-Grace organiste at the time Achille Philip, “organiste titulaire du Val-de-Grâce de 1903 à 1950 et professeur d’orgue et d’harmonie à la Schola Cantorum de 1904 à 1950”, be called ‘Mister Modulo’ in the wedding-invitations line “L’orgue sera tenu par Monsieur Modulo”???

Again, the late Norbert Dufourcq comes to our rescue, proposing a good candidate for ‘Monsieur Modulo’ : “As for “modulo”, note that the organist at Notre-Dame at that time, Léonce de Saint-Martin, was also the composer of a “Suite Cyclique”, though I admit that this is just wordplay: there is nothing “modular” about this work. Maybe a more serious candidate would be Olivier Messiaen (who was organist at the Église de la Trinité): his “modes à transposition limitée” are really about Z/12Z→Z/3Z and Z/12Z→Z/4Z. “

Messiaen’s ‘Modes of limited transposition’ were compiled in his book ‘Technique de mon langage musical’. This book was published in Paris by Leduc, as late as 1944, 5 years after the wedding-invitation.

Still, several earlier works of Messiaen used these schemes, most notably La Nativité du Seigneur, composed in 1935 : “The work is one of the earliest to feature elements that were to become key to Messiaen’s later compositions, such as the extensive use of the composer’s own modes of limited transposition, as well as influence from birdsong, and the meters and rhythms of Ancient Greek and traditional Indian music.”

More details on Messiaen’s modes and their connection to modular arithmetic can be found in the study Implementing Modality in Algorithmic Composition by Vincent Joseph Manzo.

Hence, Messiaen is a suitable candidate for the title ‘Monsieur Modulo’, but would he be able to play the Val-de-Grace organ while not being the resident organist?

Remember, the Val-de-Grace church was the concert hall of La Schola, and its musical organ the instrument of choice for the relevant courses. Now … Olivier Messiaen taught at the Schola Cantorum and the École Normale de Musique from 1936 till 1939. So, at the time of the Bourbaki-Petard wedding he would certainly be allowed to play the Cavaillé-Coll organ.

Perhaps we got it right, the second time around : the Bourbaki-Pétard wedding was held on June 3rd 1939 in the church ‘l’église royale Notre-Dame du Val-de-Grâce’ at 12h?

3 Comments

Views of noncommutative spaces

Published May 18, 2009 by lievenlb

The general public expects pictures from geometers, even from non-commutative geometers. Hence, it is important for researchers in this topic to make an attempt to convey the mental picture they have of their favourite noncommutative space, … somehow. Two examples :

This picture was created by Shahn Majid. It appears on his visions of noncommutative geometry page as well as in an extremely readable Plus-magazine article on Quantum geometry, written by Marianne Freiberger, explaining Shahn’s ideas. For more information on this, read Shahn’s SpaceTime blog.

This painting is Jackson Pollock‘s “Untitled N.3”. It depicts the way Matilde Marcolli imagines a noncommutative space. It is taken from her slides of her talk for a general audience Mathematicians look at particle physics.

3 Comments

Mumford’s treasure map

Published December 13, 2008 by lievenlb

David Mumford did receive earlier this year the 2007 AMS Leroy P. Steele Prize for Mathematical Exposition. The jury honors Mumford for “his beautiful expository accounts of a host of aspects of algebraic geometry”. Not surprisingly, the first work they mention are his mimeographed notes of the first 3 chapters of a course in algebraic geometry, usually called “Mumford’s red book” because the notes were wrapped in a red cover. In 1988, the notes were reprinted by Springer-Verlag. Unfortnately, the only red they preserved was in the title.

The AMS describes the importance of the red book as follows. “This is one of the few books that attempt to convey in pictures some of the highly abstract notions that arise in the field of algebraic geometry. In his response upon receiving the prize, Mumford recalled that some of his drawings from The Red Book were included in a collection called Five Centuries of French Mathematics. This seemed fitting, he noted: “After all, it was the French who started impressionist painting and isn’t this just an impressionist scheme for rendering geometry?””

These days it is perfectly possible to get a good grasp on difficult concepts from algebraic geometry by reading blogs, watching YouTube or plugging in equations to sophisticated math-programs. In the early seventies though, if you wanted to know what Grothendieck’s scheme-revolution was all about you had no choice but to wade through the EGA’s and SGA’s and they were notorious for being extremely user-unfriendly regarding illustrations…

So the few depictions of schemes available, drawn by people sufficiently fluent in Grothendieck’s new geometric language had no less than treasure-map-cult-status and were studied in minute detail. Mumford’s red book was a gold mine for such treasure maps. Here’s my favorite one, scanned from the original mimeographed notes (it looks somewhat tidier in the Springer-version)

It is the first depiction of $\mathbf{spec}(\mathbb{Z}[x]) $, the affine scheme of the ring $\mathbb{Z}[x] $ of all integral polynomials. Mumford calls it the”arithmetic surface” as the picture resembles the one he made before of the affine scheme $\mathbf{spec}(\mathbb{C}[x,y]) $ corresponding to the two-dimensional complex affine space $\mathbb{A}^2_{\mathbb{C}} $. Mumford adds that the arithmetic surface is ‘the first example which has a real mixing of arithmetic and geometric properties’.

Let’s have a closer look at the treasure map. It introduces some new signs which must have looked exotic at the time, but have since become standard tools to depict algebraic schemes.

For starters, recall that the underlying topological space of $\mathbf{spec}(\mathbb{Z}[x]) $ is the set of all prime ideals of the integral polynomial ring $\mathbb{Z}[x] $, so the map tries to list them all as well as their inclusions/intersections.

The doodle in the right upper corner depicts the ‘generic point’ of the scheme. That is, the geometric object corresponding to the prime ideal $~(0) $ (note that $\mathbb{Z}[x] $ is an integral domain). Because the zero ideal is contained in any other prime ideal, the algebraic/geometric mantra (“inclusions reverse when shifting between algebra and geometry”) asserts that the gemetric object corresponding to $~(0) $ should contain all other geometric objects of the arithmetic plane, so it is just the whole plane! Clearly, it is rather senseless to depict this fact by coloring the whole plane black as then we wouldn’t be able to see the finer objects. Mumford’s solution to this is to draw a hairy ball, which in this case, is sufficiently thick to include fragments going in every possible direction. In general, one should read these doodles as saying that the geometric object represented by this doodle contains all other objects seen elsewhere in the picture if the hairy-ball-doodle includes stuff pointing in the direction of the smaller object. So, in the case of the object corresponding to $~(0) $, the doodle has pointers going everywhere, saying that the geometric object contains all other objects depicted.

Let’s move over to the doodles in the lower right-hand corner. They represent the geometric object corresponding to principal prime ideals of the form $~(p(x)) $, where $p(x) $ in an irreducible polynomial over the integers, that is, a polynomial which we cannot write as the product of two smaller integral polynomials. The objects corresponding to such prime ideals should be thought of as ‘horizontal’ curves in the plane.

The doodles depicted correspond to the prime ideal $~(x) $, containing all polynomials divisible by $x $ so when we divide it out we get, as expected, a domain $\mathbb{Z}[x]/(x) \simeq \mathbb{Z} $, and the one corresponding to the ideal $~(x^2+1) $, containing all polynomials divisible by $x^2+1 $, which can be proved to be a prime ideals of $\mathbb{Z}[x] $ by observing that after factoring out we get $\mathbb{Z}[x]/(x^2+1) \simeq \mathbb{Z}[i] $, the domain of all Gaussian integers $\mathbb{Z}[i] $. The corresponding doodles (the ‘generic points’ of the curvy-objects) have a predominant horizontal component as they have the express the fact that they depict horizontal curves in the plane. It is no coincidence that the doodle of $~(x^2+1) $ is somewhat bulkier than the one of $~(x) $ as the later one must only depict the fact that all points lying on the straight line to its left belong to it, whereas the former one must claim inclusion of all points lying on the ‘quadric’ it determines.

Apart from these ‘horizontal’ curves, there are also ‘vertical’ lines corresponding to the principal prime ideals $~(p) $, containing the polynomials, all of which coefficients are divisible by the prime number $p $. These are indeed prime ideals of $\mathbb{Z}[x] $, because their quotients are
$\mathbb{Z}[x]/(p) \simeq (\mathbb{Z}/p\mathbb{Z})[x] $ are domains, being the ring of polynomials over the finite field $\mathbb{Z}/p\mathbb{Z} = \mathbb{F}_p $. The doodles corresponding to these prime ideals have a predominant vertical component (depicting the ‘vertical’ lines) and have a uniform thickness for all prime numbers $p $ as each of them only has to claim ownership of the points lying on the vertical line under them.

Right! So far we managed to depict the zero prime ideal (the whole plane) and the principal prime ideals of $\mathbb{Z}[x] $ (the horizontal curves and the vertical lines). Remains to depict the maximal ideals. These are all known to be of the form
$\mathfrak{m} = (p,f(x)) $
where $p $ is a prime number and $f(x) $ is an irreducible integral polynomial, which remains irreducible when reduced modulo $p $ (that is, if we reduce all coefficients of the integral polynomial $f(x) $ modulo $p $ we obtain an irreducible polynomial in $~\mathbb{F}_p[x] $). By the algebra/geometry mantra mentioned before, the geometric object corresponding to such a maximal ideal can be seen as the ‘intersection’ of an horizontal curve (the object corresponding to the principal prime ideal $~(f(x)) $) and a vertical line (corresponding to the prime ideal $~(p) $). Because maximal ideals do not contain any other prime ideals, there is no reason to have a doodle associated to $\mathfrak{m} $ and we can just depict it by a “point” in the plane, more precisely the intersection-point of the horizontal curve with the vertical line determined by $\mathfrak{m}=(p,f(x)) $. Still, Mumford’s treasure map doesn’t treat all “points” equally. For example, the point corresponding to the maximal ideal $\mathfrak{m}_1 = (3,x+2) $ is depicted by a solid dot $\mathbf{.} $, whereas the point corresponding to the maximal ideal $\mathfrak{m}_2 = (3,x^2+1) $ is represented by a fatter point $\circ $. The distinction between the two ‘points’ becomes evident when we look at the corresponding quotients (which we know have to be fields). We have

$\mathbb{Z}[x]/\mathfrak{m}_1 = \mathbb{Z}[x]/(3,x+2)=(\mathbb{Z}/3\mathbb{Z})[x]/(x+2) = \mathbb{Z}/3\mathbb{Z} = \mathbb{F}_3 $ whereas $\mathbb{Z}[x]/\mathfrak{m}_2 = \mathbb{Z}[x]/(3,x^2+1) = \mathbb{Z}/3\mathbb{Z}[x]/(x^2+1) = \mathbb{F}_3[x]/(x^2+1) = \mathbb{F}_{3^2} $

because the polynomial $x^2+1 $ remains irreducible over $\mathbb{F}_3 $, the quotient $\mathbb{F}_3[x]/(x^2+1) $ is no longer the prime-field $\mathbb{F}_3 $ but a quadratic field extension of it, that is, the finite field consisting of 9 elements $\mathbb{F}_{3^2} $. That is, we represent the ‘points’ lying on the vertical line corresponding to the principal prime ideal $~(p) $ by a solid dot . when their quotient (aka residue field is the prime field $~\mathbb{F}_p $, by a bigger point $\circ $ when its residue field is the finite field $~\mathbb{F}_{p^2} $, by an even fatter point $\bigcirc $ when its residue field is $~\mathbb{F}_{p^3} $ and so on, and on. The larger the residue field, the ‘fatter’ the corresponding point.

In fact, the ‘fat-point’ signs in Mumford’s treasure map are an attempt to depict the fact that an affine scheme contains a lot more information than just the set of all prime ideals. In fact, an affine scheme determines (and is determined by) a “functor of points”. That is, to every field (or even every commutative ring) the affine scheme assigns the set of its ‘points’ defined over that field (or ring). For example, the $~\mathbb{F}_p $-points of $\mathbf{spec}(\mathbb{Z}[x]) $ are the solid . points on the vertical line $~(p) $, the $~\mathbb{F}_{p^2} $-points of $\mathbf{spec}(\mathbb{Z}[x]) $ are the solid . points and the slightly bigger $\circ $ points on that vertical line, and so on.

This concludes our first attempt to decypher Mumford’s drawing, but if we delve a bit deeper, we are bound to find even more treasures… (to be continued).

5 Comments