Skip to content →

Tag: non-commutative

Views of noncommutative spaces

Published May 18, 2009 by lievenlb

The general public expects pictures from geometers, even from non-commutative geometers. Hence, it is important for researchers in this topic to make an attempt to convey the mental picture they have of their favourite noncommutative space, … somehow. Two examples :



This picture was created by Shahn Majid. It appears on his visions of noncommutative geometry page as well as in an extremely readable Plus-magazine article on Quantum geometry, written by Marianne Freiberger, explaining Shahn’s ideas. For more information on this, read Shahn’s SpaceTime blog.



This painting is Jackson Pollock‘s “Untitled N.3”. It depicts the way Matilde Marcolli imagines a noncommutative space. It is taken from her slides of her talk for a general audience Mathematicians look at particle physics.

3 Comments

F_un with Manin

Published September 10, 2008 by lievenlb

Amidst all LHC-noise, Yuri I. Manin arXived today an interesting paper Cyclotomy and analytic geometry over $\mathbb{F}_1 $.

The paper gives a nice survey of the existent literature and focusses on the crucial role of roots of unity in the algebraic geometry over the non-existent field with one element $\mathbb{F}_1 $ (in French called ‘F-un’). I have tried to do a couple of posts on F-un some time ago but now realize, reading Manin’s paper, I may have given up way too soon…

At several places in the paper, Manin hints at a possible noncommutative geometry over $\mathbb{F}_1 $ :

This is the appropriate place to stress that in a wider context of Toen-Vaqui ‘Au-dessous de Spec Z’, or eventually in noncommutative $\mathbb{F}_1 $-geometry, teh spectrum of $\mathbb{F}_1 $ loses its privileged position as a final object of a geometric category. For example, in noncommutative geometry, or in an appropriate category of stacks, the quotient of this spectrum modulo the trivial action of a group must lie below this spectrum.

Soule’s algebras $\mathcal{A}_X $ are a very important element of the structure, in particular, because they form a bridge to Arakelov geometry. Soule uses concrete choices of them in order to produce ‘just right’ supply of morphisms, without a priori constraining these choices formally. In this work, we use these algebras and their version also to pave a way to the analytic (and possibly non-commutative) geometry over $\mathbb{F}_1 $.

Back when I was writing the first batch of F-un posts, I briefly contemplated the possibility of a noncommutative geometry over $\mathbb{F}_1 $, but quickly forgot about it because I thought it would be forced to reduce to commutative geometry.

Here is the quick argument : noncommutative geometry is really the study of coalgebras (see for example my paper or if you prefer more trustworthy sources the Kontsevich-Soibelman paper). Now, unless I made a mistake, I think all coalgebras over $\mathbb{F}_1 $ must be co-commutative (even group-like), so reducing to commutative geometry.

Surely, I’m missing something…

9 Comments

the Manin-Marcolli cave

Published March 28, 2007 by lievenlb

Yesterday, Yuri Manin and Matilde Marcolli arXived their paper
Modular shadows and the Levy-Mellin infinity-adic transform which is a
follow-up of their previous paper Continued fractions, modular symbols, and non-commutative geometry.
They motivate the title of the recent paper by :

In
[MaMar2](http://www.arxiv.org/abs/hep-th/0201036), these and similar
results were put in connection with the so called “holography”
principle in modern theoretical physics. According to this principle,
quantum field theory on a space may be faithfully reflected by an
appropriate theory on the boundary of this space. When this boundary,
rather than the interior, is interpreted as our observable
space‚Äìtime, one can proclaim that the ancient Plato’s cave metaphor
is resuscitated in this sophisticated guise. This metaphor motivated
the title of the present paper.

Here’s a layout of
Plato’s cave

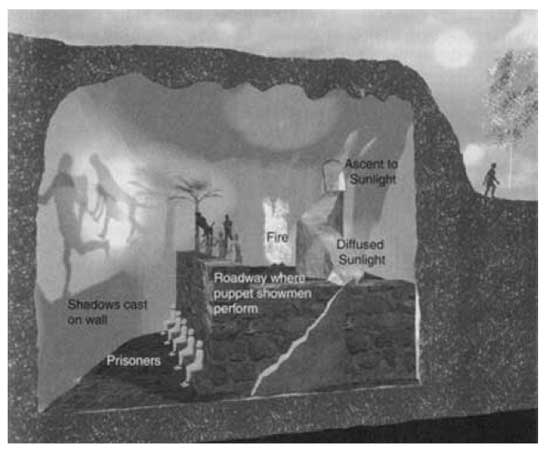
Imagine prisoners, who have been chained since childhood deep inside an
cave: not only are their limbs immobilized by the chains; their heads
are chained as well, so that their gaze is fixed on a wall.
Behind
the prisoners is an enormous fire, and between the fire and the
prisoners is a raised walkway, along which statues of various animals,
plants, and other things are carried by people. The statues cast shadows
on the wall, and the prisoners watch these shadows. When one of the
statue-carriers speaks, an echo against the wall causes the prisoners to
believe that the words come from the shadows.
The prisoners
engage in what appears to us to be a game: naming the shapes as they
come by. This, however, is the only reality that they know, even though
they are seeing merely shadows of images. They are thus conditioned to
judge the quality of one another by their skill in quickly naming the
shapes and dislike those who begin to play poorly.
Suppose a
prisoner is released and compelled to stand up and turn around. At that
moment his eyes will be blinded by the firelight, and the shapes passing
will appear less real than their shadows.

Right, now how
does the Manin-Marcolli cave look? My best guess is : like this
picture, taken from Curt McMullen’s Gallery

Imagine
this as the top view of a spherical cave. M&M are imprisoned in the
cave, their heads chained preventing them from looking up and see the
ceiling (where $PSL_2(\mathbb{Z}) $ (or a cofinite subgroup of
it) is acting on the upper-half plane via
Moebius-transformations ). All they can see is the circular exit of the
cave. They want to understand the complex picture going on over their
heads from the only things they can observe, that is the action of
(subgroups of) the modular group on the cave-exit
$\mathbb{P}^1(\mathbb{R}) $. Now, the part of it consisting
of orbits of cusps
$\mathbb{P}^1(\mathbb{Q}) $ has a nice algebraic geometric
description, but orbits of irrational points cannot be handled by
algebraic geometry as the action of $PSL_2(\mathbb{Z}) $ is
highly non-discrete as illustrated by another picture from McMullen’s
gallery

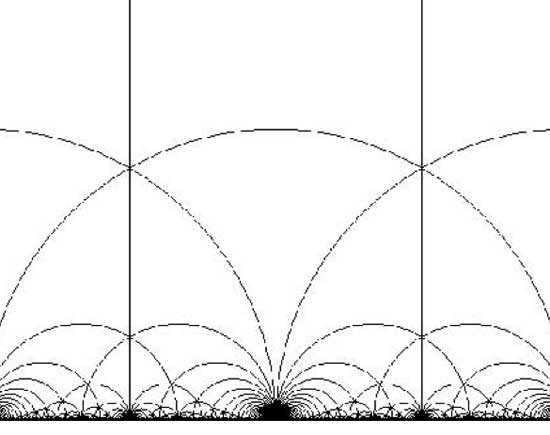
depicting the ill behaved topology of the action on the bottom real
axis. Still, noncommutative _differential_ geometry is pretty good at
handling such ill behaved quotient spaces and it turns out that as a
noncommutative space, this quotient
$\mathbb{P}^1(\mathbb{R})/PSL_2(\mathbb{Z}) $ is rich enough
to recover many important aspects of the classical theory of modular
curves. Hence, they reverse the usual NCG-picture of interpreting
commutative objects as shadows of noncommutative ones. They study the
_noncommutative shadow_
$\mathbb{P}^1(\mathbb{R})/PSL_2(\mathbb{Z}) $ of a classical
commutative object, the quotient of the action of the modular group (or
a cofinite subgroup of it) on the upper half-plane.

In our
noncommutative geometry course we have already
seen this noncommutative shadow in action (though at a very basic
level). Remember that we first described the group-structure of the
modular group $PSL_2(\mathbb{Z}) = C_2 \ast C_3 $ via the
classical method of groups acting on trees. In particular, we
considered the tree

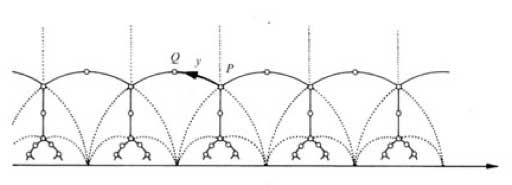
and
calculated the stabilizers of the end points of its fundamental domain
(the thick circular edge). But
later we were able to give a
much shorter proof (due to Roger Alperin) by looking only at the action
of $PSL_2(\mathbb{Z}) $ on the irrational real numbers (the
noncommutative shadow). Needless to say that the results obtained by
Manin and Marcolli from staring at their noncommutative shadow are a lot
more intriguing…

One Comment