Skip to content →

Tag: nim

n-dimensional and transfinite Nimbers

Published January 8, 2011 by lievenlb

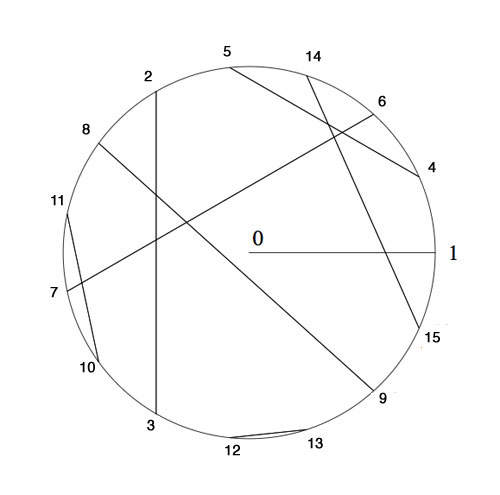
Today, we will expand the game of Nimbers to higher dimensions and do some transfinite Nimber hacking.

In our identification between $\mathbb{F}_{16}^* $ and 15-th roots of unity, the number 8 corresponds to $\mu^6 $, whence $\sqrt{8}=\mu^3=14 $. So, if we add a stone at the diagonal position (14,14) to the Nimbers-position of last time

we get a position of Nim-value 0, that is, winnable for the second player. In fact, this is a universal Nimbers-truth :

Either the 2nd player wins a Nimbers-position, or one can add one stone to the diagonal such that it becomes a 2nd player win.

The proof is elementary : choose a Fermat 2-power such that all stones have coordinates smaller than $2^{2^n} $. If the Nim-value of the position isn’t zero, it corresponds to a unit $\alpha \in \mathbb{F}_{2^{2^n}}^* $. Now,the Frobenius map $x \mapsto x^2 $ is an automorphism of any finite field of characteristic two, so the square root $\sqrt{\alpha} $ also belongs to $\mathbb{F}_{2^{2^n}} $, done!

3-dimensional Nimbers is played in the first octant of the integral lattice $\mathbb{Z}^3 $ by placing a finite number of balls at places $~(a,b,c) \in \mathbb{N}^3 $ with $abc \geq 1 $.

Moves are defined by replacing the rectangular-rule of the two-dimensional version by the cuboid-rule : take a cuboid with faces parallel to the coordinate planes whose corner of maximal distance from the origin is one of the balls in the position. Remove that ball and add new balls to the unoccupied corners and remove balls at occupied corners.

Here, we allow the corner-points to have zero as some of its coordinates, but these balls are considered dead in the game. As in the two-dimensional game, this cuboid-rule encompasses several legal moves depending on the number of corners in the cuboid having zero-coordinates.

Again, it follows by induction that the Nim-value of a ball placed at position $~(a,b,c) $ is equal to the Nim-multiplication $a \otimes b \otimes c $ and we can calculate the Nim-value of a 3-dimensional Nimbers-position by computing in a suitable field $\mathbb{F}_{2^{2^n}} $. (The extension to higher dimensions is now obvious)

Does 3-dimensional Nimbers satisfy the ‘universal truth’, that is, can one make any position a 2nd player win by adding at most one stone to the body-diagonal?

The previous argument fails. As $\mathbb{F}_4^* $ is the cyclic group of order three, the 3rd roots of unity in $\overline{\mathbb{F}_2} $ correspond to the numbers 1,2 and 3, so the map $x \mapsto x^3 $ cannot be a bijection on any of the finite fields $\mathbb{F}_{2^{2^n}} $.

But then, perhaps, a third root is added by going to a larger such field $\mathbb{F}_{2^{2^N}} $? Well, not quite. Take for example 2, then $\sqrt[3]{2} \notin \mathbb{F}_{2^{2^N}} $. (2 has order 3 in $\mathbb{F}_4 $ and so its 3rd root must have order 9, but 9 does not divide any number of the form $2^{2^N}-1 $ as the Fermat-powers mod 9 can only be 4 or 7).

In fact one can show that this also holds for any number not in the image of the cubing-map in some $\mathbb{F}_{2^{2^n}} $ as

$\mathbb{N}={ 0,1,2,\ldots } = \cup_N \mathbb{F}_{2^{2^N}} $

with Nim-addition and multiplication is the quadratic closure of $\mathbb{F}_2 $ (see for example ONAG).

The situation changes if we allow ourself to play transfinite Nimbers, with the same rules as before but now we allow the stone, balls etc. to be placed at points of which the coordinates are not restricted to $\mathbb{N}_+ = \{ 1,2,3,\ldots \} $ but may vary over $[\beta]_+ $ for some ordinal $\beta $ where $[\beta]_+=\{ 1,2,\ldots,\omega,\omega+1,\ldots \} $ is the set of all ordinals smaller than $\beta $.

In transfinite 3-dimensional Nimbers the ‘universal truth’ still holds, provided we play it on a cube of sizes $[\omega^{\omega}]_+ $. In particular we have that $\sqrt[3]{2}=\omega $ by the simplicity rule (see ONAG or the Conway’s nim-arithmetic post)

In general, n-dimensional transfinite Nimbers played on an n-gid of sizes $[\omega^{\omega^{\omega}}]_+ $ satisfies the universal truth : either a position is a 2nd player win or it becomes one by adding one n-ball to a diagonal position! (this follows immediately because $[\omega^{\omega^{\omega}}] $ with Nim-addition and multiplication is isomorphic to the algebraic closure of $\mathbb{F}_2 $).

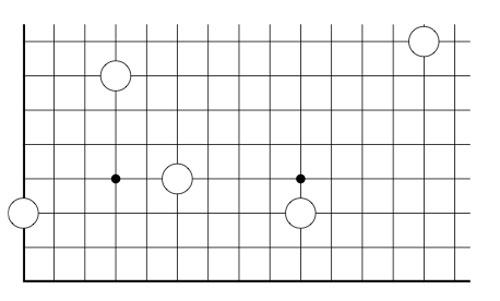
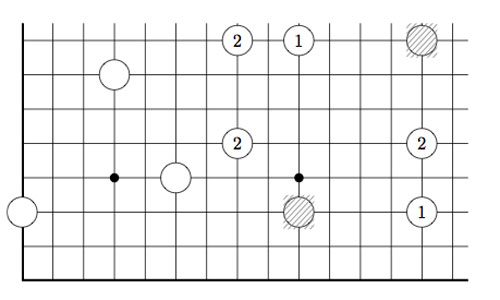
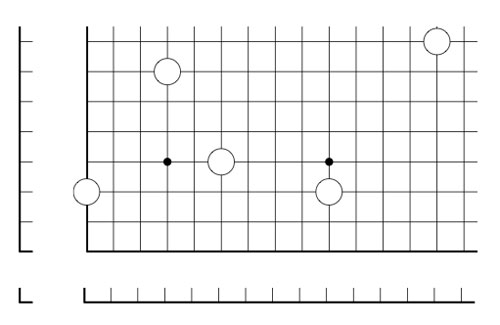
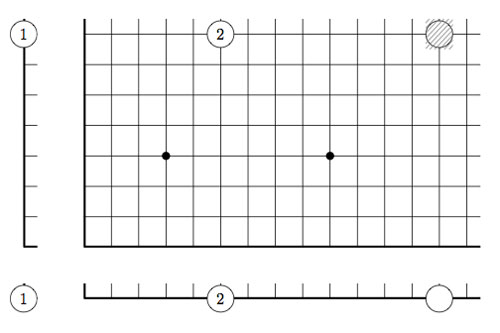
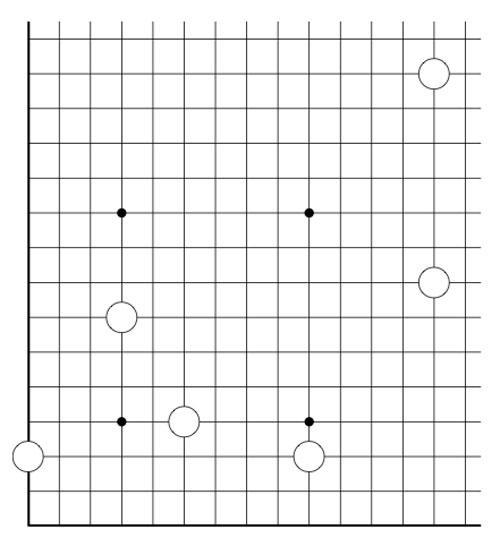
2-dimensional transfinite Nimbers is still pretty playable. Below a position on a $\omega.2 $-board with stones as positions $~(2,2),(4,\omega),(\omega+2,\omega+3) $ and $~(\omega+4,\omega+1) $

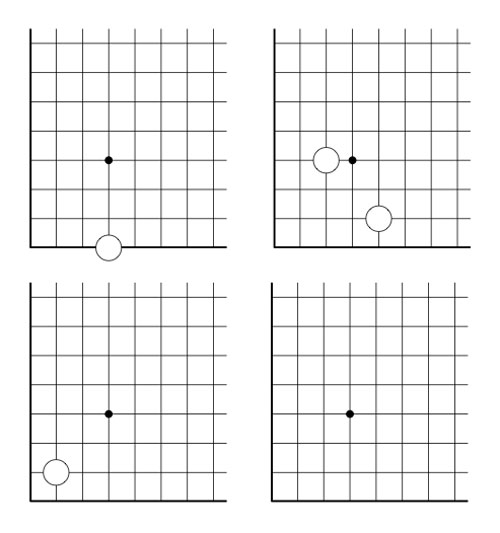
Give a winning move for the first player!

Leave a Comment

How to play Nimbers?

Published January 7, 2011 by lievenlb

Nimbers is a 2-person game, winnable only if you understand the arithmetic of the finite fields $\mathbb{F}_{2^{2^n}} $ associated to Fermat 2-powers.

It is played on a rectangular array (say a portion of a Go-board, for practical purposes) having a finite number of stones at distinct intersections. Here’s a typical position

The players alternate making a move, which is either

  • removing one stone, or
  • moving a stone to a spot on the same row (resp. the same column) strictly to the left (resp. strictly lower), and if there’s already a stone on this spot, both stones are removed, or
  • adding stones to the empty corners of a rectangle having as its top-right hand corner a chosen stone and removing stones at the occupied corners

Here we illustrate two possible moves from the above position, in the first we add two new stones and remove 2 existing stones, in the second we add three new stones and remove only the top right-hand stone.

As always, the last player able to move wins the game!

Note that Nimbers is equivalent to Lenstra’s ‘turning corners’-game (as introduced in his paper Nim-multiplication or mentioned in Winning Ways Chapter 14, page 473).

If all stones are placed on the left-most column (or on the bottom row) one quickly realizes that this game reduces to classical Nim with Nim-heap sizes corresponding to the stones (for example, the left-most stone corresponds to a heap of size 3).

Nim-addition $n \oplus m $ is defined inductively by

$n \oplus m = mex(n’ \oplus m,n \oplus m’) $

where $n’ $ is any element of ${ 0,1,\ldots,n-1 } $ and $m’ $ any element of ${ 0,1,\ldots,m-1 } $ and where ‘mex’ stands for Minimal EXcluded number, that is the smallest natural number which isn’t included in the set. Alternatively, one can compute $n \oplus m $ buy writing $n $ and $m $ in binary and add these binary numbers without carrying-over. It is well known that a winning strategy for Nim tries to shorten one Nim-heap such that the Nim-addition of the heap-sizes equals zero.

This allows us to play Nimber-endgames, that is, when all the stones have been moved to the left-column or the bottom row.

To evaluate general Nimber-positions it is best to add another row and column, the coordinate axes of the array

and so our stones lie at positions (1,3), (4,7), (6,4), (10,3) and (14,8). In this way all legal moves follow the rectangle-rule when we allow rectangles to contain corners on the added coordinate axes. For example, removing a stone is achieved by taking a rectangle with two sides on the added axes, and, moving a stone to the left (or the bottom) is done by taking a rectangle with one side at the x-axes (resp. the y-axes)

However, the added stones on the coordinate axes are considered dead and may be removed from the game. This observation allows us to compute the Grundy number of a stone at position (m,n) to be

$G(m,n)=mex(G(m’,n’) \oplus G(m’,n) \oplus G(m,n’)~:~0 \leq m’ < m, 0 \leq n’ < n) $

and so by induction these Grundy numbers are equal to the Nim-multiplication $G(m,n) = m \otimes n $ where

$m \otimes n = mex(m’ \otimes n’ \oplus m’ \otimes n \oplus m \otimes n’~:~0 \leq m’ < m, 0 \leq n’ < n) $

Thus, we can evaluate any Nimbers-position with stone-coordinates smaller than $2^{2^n} $ by calculating in a finite field using the identification (as for example in the odd Knights of the round table-post) $\mathbb{F}_{2^{2^n}} = \{ 0,1,2,\ldots,2^{2^n}-1 \} $

For example, when all stones lie in a 15×15 grid (as in the example above), all calculations can be performed using

Here, we’ve identified the non-zero elements of $\mathbb{F}_{16} $ with 15-th roots of unity, allowing us to multiply, and we’ve paired up couples $(n,n \oplus 1) $ allowing u to reduce nim-addition to nim-multiplication via

$n \oplus m = (n \otimes \frac{1}{m}) \otimes (m \oplus 1) $

In particular, the stone at position (14,8) is equivalent to a Nim-heap of size $14 \otimes 8=10 $. The nim-value of the original position is equal to 8

Suppose your opponent lets you add one extra stone along the diagonal if you allow her to start the game, where would you have to place it and be certain you will win the game?

One Comment