Tag: modular

Mumford’s treasure map

Published December 13, 2008 by lievenlb

David Mumford did receive earlier this year the 2007 AMS Leroy P. Steele Prize for Mathematical Exposition. The jury honors Mumford for “his beautiful expository accounts of a host of aspects of algebraic geometry”. Not surprisingly, the first work they mention are his mimeographed notes of the first 3 chapters of a course in algebraic geometry, usually called “Mumford’s red book” because the notes were wrapped in a red cover. In 1988, the notes were reprinted by Springer-Verlag. Unfortnately, the only red they preserved was in the title.

The AMS describes the importance of the red book as follows. “This is one of the few books that attempt to convey in pictures some of the highly abstract notions that arise in the field of algebraic geometry. In his response upon receiving the prize, Mumford recalled that some of his drawings from The Red Book were included in a collection called Five Centuries of French Mathematics. This seemed fitting, he noted: “After all, it was the French who started impressionist painting and isn’t this just an impressionist scheme for rendering geometry?””

These days it is perfectly possible to get a good grasp on difficult concepts from algebraic geometry by reading blogs, watching YouTube or plugging in equations to sophisticated math-programs. In the early seventies though, if you wanted to know what Grothendieck’s scheme-revolution was all about you had no choice but to wade through the EGA’s and SGA’s and they were notorious for being extremely user-unfriendly regarding illustrations…

So the few depictions of schemes available, drawn by people sufficiently fluent in Grothendieck’s new geometric language had no less than treasure-map-cult-status and were studied in minute detail. Mumford’s red book was a gold mine for such treasure maps. Here’s my favorite one, scanned from the original mimeographed notes (it looks somewhat tidier in the Springer-version)

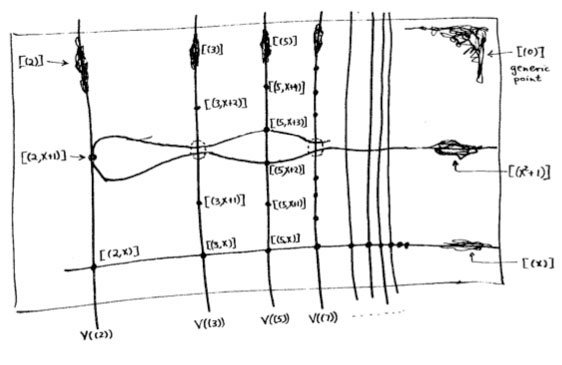
It is the first depiction of $\mathbf{spec}(\mathbb{Z}[x]) $, the affine scheme of the ring $\mathbb{Z}[x] $ of all integral polynomials. Mumford calls it the”arithmetic surface” as the picture resembles the one he made before of the affine scheme $\mathbf{spec}(\mathbb{C}[x,y]) $ corresponding to the two-dimensional complex affine space $\mathbb{A}^2_{\mathbb{C}} $. Mumford adds that the arithmetic surface is ‘the first example which has a real mixing of arithmetic and geometric properties’.

Let’s have a closer look at the treasure map. It introduces some new signs which must have looked exotic at the time, but have since become standard tools to depict algebraic schemes.

For starters, recall that the underlying topological space of $\mathbf{spec}(\mathbb{Z}[x]) $ is the set of all prime ideals of the integral polynomial ring $\mathbb{Z}[x] $, so the map tries to list them all as well as their inclusions/intersections.

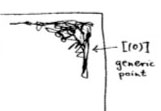The doodle in the right upper corner depicts the ‘generic point’ of the scheme. That is, the geometric object corresponding to the prime ideal $~(0) $ (note that $\mathbb{Z}[x] $ is an integral domain). Because the zero ideal is contained in any other prime ideal, the algebraic/geometric mantra (“inclusions reverse when shifting between algebra and geometry”) asserts that the gemetric object corresponding to $~(0) $ should contain all other geometric objects of the arithmetic plane, so it is just the whole plane! Clearly, it is rather senseless to depict this fact by coloring the whole plane black as then we wouldn’t be able to see the finer objects. Mumford’s solution to this is to draw a hairy ball, which in this case, is sufficiently thick to include fragments going in every possible direction. In general, one should read these doodles as saying that the geometric object represented by this doodle contains all other objects seen elsewhere in the picture if the hairy-ball-doodle includes stuff pointing in the direction of the smaller object. So, in the case of the object corresponding to $~(0) $, the doodle has pointers going everywhere, saying that the geometric object contains all other objects depicted.

Let’s move over to the doodles in the lower right-hand corner. They represent the geometric object corresponding to principal prime ideals of the form $~(p(x)) $, where $p(x) $ in an irreducible polynomial over the integers, that is, a polynomial which we cannot write as the product of two smaller integral polynomials. The objects corresponding to such prime ideals should be thought of as ‘horizontal’ curves in the plane.

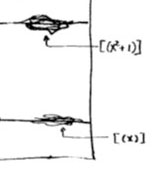
The doodles depicted correspond to the prime ideal $~(x) $, containing all polynomials divisible by $x $ so when we divide it out we get, as expected, a domain $\mathbb{Z}[x]/(x) \simeq \mathbb{Z} $, and the one corresponding to the ideal $~(x^2+1) $, containing all polynomials divisible by $x^2+1 $, which can be proved to be a prime ideals of $\mathbb{Z}[x] $ by observing that after factoring out we get $\mathbb{Z}[x]/(x^2+1) \simeq \mathbb{Z}[i] $, the domain of all Gaussian integers $\mathbb{Z}[i] $. The corresponding doodles (the ‘generic points’ of the curvy-objects) have a predominant horizontal component as they have the express the fact that they depict horizontal curves in the plane. It is no coincidence that the doodle of $~(x^2+1) $ is somewhat bulkier than the one of $~(x) $ as the later one must only depict the fact that all points lying on the straight line to its left belong to it, whereas the former one must claim inclusion of all points lying on the ‘quadric’ it determines.

Apart from these ‘horizontal’ curves, there are also ‘vertical’ lines corresponding to the principal prime ideals $~(p) $, containing the polynomials, all of which coefficients are divisible by the prime number $p $. These are indeed prime ideals of $\mathbb{Z}[x] $, because their quotients are
$\mathbb{Z}[x]/(p) \simeq (\mathbb{Z}/p\mathbb{Z})[x] $ are domains, being the ring of polynomials over the finite field $\mathbb{Z}/p\mathbb{Z} = \mathbb{F}_p $. The doodles corresponding to these prime ideals have a predominant vertical component (depicting the ‘vertical’ lines) and have a uniform thickness for all prime numbers $p $ as each of them only has to claim ownership of the points lying on the vertical line under them.

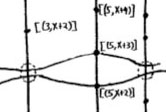Right! So far we managed to depict the zero prime ideal (the whole plane) and the principal prime ideals of $\mathbb{Z}[x] $ (the horizontal curves and the vertical lines). Remains to depict the maximal ideals. These are all known to be of the form
$\mathfrak{m} = (p,f(x)) $
where $p $ is a prime number and $f(x) $ is an irreducible integral polynomial, which remains irreducible when reduced modulo $p $ (that is, if we reduce all coefficients of the integral polynomial $f(x) $ modulo $p $ we obtain an irreducible polynomial in $~\mathbb{F}_p[x] $). By the algebra/geometry mantra mentioned before, the geometric object corresponding to such a maximal ideal can be seen as the ‘intersection’ of an horizontal curve (the object corresponding to the principal prime ideal $~(f(x)) $) and a vertical line (corresponding to the prime ideal $~(p) $). Because maximal ideals do not contain any other prime ideals, there is no reason to have a doodle associated to $\mathfrak{m} $ and we can just depict it by a “point” in the plane, more precisely the intersection-point of the horizontal curve with the vertical line determined by $\mathfrak{m}=(p,f(x)) $. Still, Mumford’s treasure map doesn’t treat all “points” equally. For example, the point corresponding to the maximal ideal $\mathfrak{m}_1 = (3,x+2) $ is depicted by a solid dot $\mathbf{.} $, whereas the point corresponding to the maximal ideal $\mathfrak{m}_2 = (3,x^2+1) $ is represented by a fatter point $\circ $. The distinction between the two ‘points’ becomes evident when we look at the corresponding quotients (which we know have to be fields). We have

$\mathbb{Z}[x]/\mathfrak{m}_1 = \mathbb{Z}[x]/(3,x+2)=(\mathbb{Z}/3\mathbb{Z})[x]/(x+2) = \mathbb{Z}/3\mathbb{Z} = \mathbb{F}_3 $ whereas $\mathbb{Z}[x]/\mathfrak{m}_2 = \mathbb{Z}[x]/(3,x^2+1) = \mathbb{Z}/3\mathbb{Z}[x]/(x^2+1) = \mathbb{F}_3[x]/(x^2+1) = \mathbb{F}_{3^2} $

because the polynomial $x^2+1 $ remains irreducible over $\mathbb{F}_3 $, the quotient $\mathbb{F}_3[x]/(x^2+1) $ is no longer the prime-field $\mathbb{F}_3 $ but a quadratic field extension of it, that is, the finite field consisting of 9 elements $\mathbb{F}_{3^2} $. That is, we represent the ‘points’ lying on the vertical line corresponding to the principal prime ideal $~(p) $ by a solid dot . when their quotient (aka residue field is the prime field $~\mathbb{F}_p $, by a bigger point $\circ $ when its residue field is the finite field $~\mathbb{F}_{p^2} $, by an even fatter point $\bigcirc $ when its residue field is $~\mathbb{F}_{p^3} $ and so on, and on. The larger the residue field, the ‘fatter’ the corresponding point.

In fact, the ‘fat-point’ signs in Mumford’s treasure map are an attempt to depict the fact that an affine scheme contains a lot more information than just the set of all prime ideals. In fact, an affine scheme determines (and is determined by) a “functor of points”. That is, to every field (or even every commutative ring) the affine scheme assigns the set of its ‘points’ defined over that field (or ring). For example, the $~\mathbb{F}_p $-points of $\mathbf{spec}(\mathbb{Z}[x]) $ are the solid . points on the vertical line $~(p) $, the $~\mathbb{F}_{p^2} $-points of $\mathbf{spec}(\mathbb{Z}[x]) $ are the solid . points and the slightly bigger $\circ $ points on that vertical line, and so on.

This concludes our first attempt to decypher Mumford’s drawing, but if we delve a bit deeper, we are bound to find even more treasures… (to be continued).

5 Comments

noncommutative F_un geometry (2)

Published October 17, 2008 by lievenlb

Last time we tried to generalize the Connes-Consani approach to commutative algebraic geometry over the field with one element $\mathbb{F}_1 $ to the noncommutative world by considering covariant functors

$N~:~\mathbf{groups} \rightarrow \mathbf{sets} $

which over $\mathbb{C} $ resp. $\mathbb{Z} $ become visible by a complex (resp. integral) algebra having suitable universal properties.

However, we didn’t specify what we meant by a complex noncommutative variety (resp. an integral noncommutative scheme). In particular, we claimed that the $\mathbb{F}_1 $-‘points’ associated to the functor

$D~:~\mathbf{groups} \rightarrow \mathbf{sets} \qquad G \mapsto G_2 \times G_3 $ (here $G_n $ denotes all elements of order $n $ of $G $)

were precisely the modular dessins d’enfants of Grothendieck, but didn’t give details. We’ll try to do this now.

For algebras over a field we follow the definition, due to Kontsevich and Soibelman, of so called “noncommutative thin schemes”. Actually, the thinness-condition is implicit in both Soule’s-approach as that of Connes and Consani : we do not consider R-points in general, but only those of rings R which are finite and flat over our basering (or field).

So, what is a noncommutative thin scheme anyway? Well, its a covariant functor (commuting with finite projective limits)

$\mathbb{X}~:~\mathbf{Alg}^{fd}_k \rightarrow \mathbf{sets} $

from finite-dimensional (possibly noncommutative) $k $-algebras to sets. Now, the usual dual-space operator gives an anti-equivalence of categories

$\mathbf{Alg}^{fd}_k \leftrightarrow \mathbf{Coalg}^{fd}_k \qquad A=C^* \leftrightarrow C=A^* $

so a thin scheme can also be viewed as a contra-variant functor (commuting with finite direct limits)

$\mathbb{X}~:~\mathbf{Coalg}^{fd}_k \rightarrow \mathbf{Sets} $

In particular, we are interested to associated to any {tex]k $-algebra $A $ its representation functor :

$\mathbf{rep}(A)~:~\mathbf{Coalg}^{fd}_k \rightarrow \mathbf{Sets} \qquad C \mapsto Alg_k(A,C^*) $

This may look strange at first sight, but $C^* $ is a finite dimensional algebra and any $n $-dimensional representation of $A $ is an algebra map $A \rightarrow M_n(k) $ and we take $C $ to be the dual coalgebra of this image.

Kontsevich and Soibelman proved that every noncommutative thin scheme $\mathbb{X} $ is representable by a $k $-coalgebra. That is, there exists a unique coalgebra $C_{\mathbb{X}} $ (which they call the coalgebra of ‘distributions’ of $\mathbb{X} $) such that for every finite dimensional $k $-algebra $B $ we have

$\mathbb{X}(B) = Coalg_k(B^*,C_{\mathbb{X}}) $

In the case of interest to us, that is for the functor $\mathbf{rep}(A) $ the coalgebra of distributions is Kostant’s dual coalgebra $A^o $. This is the not the full linear dual of $A $ but contains only those linear functionals on $A $ which factor through a finite dimensional quotient.

So? You’ve exchanged an algebra $A $ for some coalgebra $A^o $, but where’s the geometry in all this? Well, let’s look at the commutative case. Suppose $A= \mathbb{C}[X] $ is the coordinate ring of a smooth affine variety $X $, then its dual coalgebra looks like

$\mathbb{C}[X]^o = \oplus_{x \in X} U(T_x(X)) $

the direct sum of all universal (co)algebras of tangent spaces at points $x \in X $. But how do we get the variety out of this? Well, any coalgebra has a coradical (being the sun of all simple subcoalgebras) and in the case just mentioned we have

$corad(\mathbb{C}[X]^o) = \oplus_{x \in X} \mathbb{C} e_x $

so every point corresponds to a unique simple component of the coradical. In the general case, the coradical of the dual coalgebra $A^o $ is the direct sum of all simple finite dimensional representations of $A $. That is, the direct summands of the coalgebra give us a noncommutative variety whose points are the simple representations, and the remainder of the coalgebra of distributions accounts for infinitesimal information on these points (as do the tangent spaces in the commutative case).

In fact, it was a surprise to me that one can describe the dual coalgebra quite explicitly, and that $A_{\infty} $-structures make their appearance quite naturally. See this paper if you’re in for the details on this.

That settles the problem of what we mean by the noncommutative variety associated to a complex algebra. But what about the integral case? In the above, we used extensively the theory of Kostant-duality which works only for algebras over fields…

Well, not quite. In the case of $\mathbb{Z} $ (or more general, of Dedekind domains) one can repeat Kostant’s proof word for word provided one takes as the definition of the dual $\mathbb{Z} $-coalgebra
of an algebra (which is $\mathbb{Z} $-torsion free)

$A^o = { f~:~A \rightarrow \mathbb{Z}~:~A/Ker(f)~\text{is finitely generated and torsion free}~} $

(over general rings there may be also variants of this duality, as in Street’s book an Quantum groups). Probably lots of people have come up with this, but the only explicit reference I have is to the first paper I’ve ever written. So, also for algebras over $\mathbb{Z} $ we can define a suitable noncommutative integral scheme (the coradical approach accounts only for the maximal ideals rather than all primes, but somehow this is implicit in all approaches as we consider only thin schemes).

Fine! So, we can make sense of the noncommutative geometrical objects corresponding to the group-algebras $\mathbb{C} \Gamma $ and $\mathbb{Z} \Gamma $ where $\Gamma = PSL_2(\mathbb{Z}) $ is the modular group (the algebras corresponding to the $G \mapsto G_2 \times G_3 $-functor). But, what might be the points of the noncommutative scheme corresponding to $\mathbb{F}_1 \Gamma $???

Well, let’s continue the path cut out before. “Points” should correspond to finite dimensional “simple representations”. Hence, what are the finite dimensional simple $\mathbb{F}_1 $-representations of $\Gamma $? (Or, for that matter, of any group $G $)

Here we come back to Javier’s post on this : a finite dimensional $\mathbb{F}_1 $-vectorspace is a finite set. A $\Gamma $-representation on this set (of n-elements) is a group-morphism

$\Gamma \rightarrow GL_n(\mathbb{F}_1) = S_n $

hence it gives a permutation representation of $\Gamma $ on this set. But then, if finite dimensional $\mathbb{F}_1 $-representations of $\Gamma $ are the finite permutation representations, then the simple ones are the transitive permutation representations. That is, the points of the noncommutative scheme corresponding to $\mathbb{F}_1 \Gamma $ are the conjugacy classes of subgroups $H \subset \Gamma $ such that $\Gamma/H $ is finite. But these are exactly the modular dessins d’enfants introduced by Grothendieck as I explained a while back elsewhere (see for example this post and others in the same series).

noncommutative F_un geometry (1)

Published October 13, 2008 by lievenlb

It is perhaps surprising that Alain Connes and Katia Consani, two icons of noncommutative geometry, restrict themselves to define commutative algebraic geometry over $\mathbb{F}_1 $, the field with one element.

My guess of why they stop there is as good as anyone’s. Perhaps they felt that there is already enough noncommutativity in Soule’s gadget-approach (the algebra $\mathcal{A}_X $ as in this post may very well be noncommutative). Perhaps they were only interested in the Bost-Connes system which can be entirely encoded in their commutative $\mathbb{F}_1 $-geometry. Perhaps they felt unsure as to what the noncommutative scheme of an affine noncommutative algebra might be. Perhaps …

Remains the fact that their approach screams for a noncommutative extension. Their basic object is a covariant functor

$N~:~\mathbf{abelian} \rightarrow \mathbf{sets} \qquad A \mapsto N(A) $

from finite abelian groups to sets, together with additional data to the effect that there is a unique minimal integral scheme associated to $N $. In a series of posts on the Connes-Consani paper (starting here) I took some care of getting rid of all scheme-lingo and rephrasing everything entirely into algebras. But then, this set-up can be extended verbatim to noncommuative $\mathbb{F}_1 $-geometry, which should start from a covariant functor

$N~:~\mathbf{groups} \rightarrow \mathbf{sets} $

from all finite groups to sets. Let’s recall quickly what the additional info should be making this functor a noncommutative (affine) F_un scheme :

There should be a finitely generated $\mathbb{C} $-algebra $R $ together with a natural transformation (the ‘evaluation’)

$e~:~N \rightarrow \mathbf{maxi}(R) \qquad N(G) \mapsto Hom_{\mathbb{C}-alg}(R, \mathbb{C} G) $

(both $R $ and the group-algebra $\mathbb{C} G $ may be noncommutative). The pair $(N, \mathbf{maxi}(R)) $ is then called a gadget and there is an obvious notion of ‘morphism’ between gadgets.

The crucial extra ingredient is an affine $\mathbb{Z} $-algebra (possibly noncommutative) $S $
such that $N $ is a subfunctor of $\mathbf{mini}(S)~:~G \mapsto Hom_{\mathbb{Z}-alg}(S,\mathbb{Z} G) $ together with the following universal property :

any affine $\mathbb{Z} $-algebra $T $ having a gadget-morphism $~(N,\mathbf{maxi}(R)) \rightarrow (\mathbf{mini}(T),\mathbf{maxi}(T \otimes_{\mathbb{Z}} \mathbb{C})) $ comes from a $\mathbb{Z} $-algebra morphism $T \rightarrow S $. (If this sounds too cryptic for you, please read the series on C-C mentioned before).

So, there is no problem in defining noncommutative affine F_un-schemes. However, as with any generalization, this only makes sense provided (a) we get something new and (b) we have interesting examples, not covered by the restricted theory.

At first sight we do not get something new as in the only example we did in the C-C-series (the forgetful functor) it is easy to prove (using the same proof as given in this post) that the forgetful-functor $\mathbf{groups} \rightarrow \mathbf{sets} $ still has as its integral form the integral torus $\mathbb{Z}[x,x^{-1}] $. However, both theories quickly diverge beyond this example.

For example, consider the functor

$\mathbf{groups} \rightarrow \mathbf{sets} \qquad G \mapsto G \times G $

Then, if we restrict to abelian finite groups $\mathbf{abelian} $ it is easy to see (again by a similar argument) that the two-dimensional integer torus $\mathbb{Z}[x,y,x^{-1},y^{-1}] $ is the correct integral form. However, this algebra cannot be the correct form for the functor on the category of all finite groups as any $\mathbb{Z} $-algebra map $\phi~:~\mathbb{Z}[x,y,x^{-1},y^{-1}] \rightarrow \mathbb{Z} G $ determines (and is determined by) a pair of commuting units in $\mathbb{Z} G $, so the above functor can not be a subfunctor if we allow non-Abelian groups.

But then, perhaps there isn’t a minimal integral $\mathbb{Z} $-form for this functor? Well, yes there is. Take the free group in two letters (that is, all words in noncommuting $x,y,x^{-1} $ and $y^{-1} $ satisfying only the trivial cancellation laws between a letter and its inverse), then the corresponding integral group-algebra $\mathbb{Z} \mathcal{F}_2 $ does the trick.

Again, the proof-strategy is the same. Given a gadget-morphism we have an algebra map $f~:~T \mapsto \mathbb{C} \mathcal{F}_2 $ and we have to show, using the universal property that the image of $T $ is contained in the integral group-algebra $\mathbb{Z} \mathcal{F}_2 $. Take a generator
$z $ of $T $ then the degree of the image $f(z) $ is bounded say by $d $ and we can always find a subgroup $H \subset \mathcal{F}_2 $ such that $\mathcal{F}_2/H $ is a fnite group and the quotient map $\mathbb{C} \mathcal{F}_2 \rightarrow \mathbb{C} \mathcal{F}_2/H $ is injective on the subspace spanned by all words of degree strictly less than $d+1 $. Then, the usual diagram-chase finishes the proof.

What makes this work is that the free group $\mathcal{F}_2 $ has ‘enough’ subgroups of finite index, a property it shares with many interesting discrete groups. Whence the blurb-message :

if the integers $\mathbb{Z} $ see a discrete group $\Gamma $, then the field $\mathbb{F}_1 $ sees its profinite completion $\hat{\Gamma} = \underset{\leftarrow}{lim}~\Gamma/ H $

So, yes, we get something new by extending the Connes-Consani approach to the noncommutative world, but do we have interesting examples? As “interesting” is a subjective qualification, we’d better invoke the authority-argument.

Alexander Grothendieck (sitting on the right, manifestly not disputing a vacant chair with Jean-Pierre Serre, drinking on the left (a marvelous picture taken by F. Hirzebruch in 1958)) was pushing the idea that profinite completions of arithmetical groups were useful in the study of the absolute Galois group $Gal(\overline{\mathbb{Q}}/\mathbb{Q}) $, via his theory of dessins d’enfants (children;s drawings).

In a previous life, I’ve written a series of posts on dessins d’enfants, so I’ll restrict here to the basics. A smooth projective $\overline{\mathbb{Q}} $-curve $X $ has a Belyi-map $X \rightarrow \mathbb{P}^1_{\overline{\mathbb{Q}}} $ ramified only in three points ${ 0,1,\infty } $. The “drawing” corresponding to $X $ is a bipartite graph, drawn on the Riemann surface $X_{\mathbb{C}} $ obtained by lifting the unit interval $[0,1] $ to $X $. As the absolute Galois group acts on all such curves (and hence on their corresponding drawings), the action of it on these dessins d’enfants may give us a way into the multiple mysteries of the absolute Galois group.

In his “Esquisse d’un programme” (Sketch of a program if you prefer to read it in English) he writes :

“C’est ainsi que mon attention s’est portée vers ce que j’ai appelé depuis la “géométrie algêbrique anabélienne”, dont le point de départ est justement une étude (pour le moment limitée à la caractéristique zéro) de l’action de groupe de Galois “absolus” (notamment les groupes $Gal(\overline{K}/K) $, ou $K $ est une extension de type fini du corps premier) sur des groupes fondamentaux géométriques (profinis) de variétés algébriques (définies sur $K $), et plus particulièrement (rompant avec une tradition bien enracinée) des groupes fondamentaux qui sont trés éloignés des groupes abéliens (et que pour cette raison je nomme “anabéliens”). Parmi ces groupes, et trés proche du groupe $\hat{\pi}_{0,3} $, il y a le compactifié profini du groupe modulaire $SL_2(\mathbb{Z}) $, dont le quotient par le centre $\pm 1 $ contient le précédent comme sous-groupe de congruence mod 2, et peut s’interpréter d’ailleurs comme groupe “cartographique” orienté, savoir celui qui classifie les cartes orientées triangulées (i.e. celles dont les faces des triangles ou des monogones).”

and a bit further, he writes :

“L’élément de structure de $SL_2(\mathbb{Z}) $ qui me fascine avant tout, est bien sur l’action extérieure du groupe de Galois $Gal(\overline{\mathbb{Q}}/\mathbb{Q}) $ sur le compactifié profini. Par le théorème de Bielyi, prenant les compactifiés profinis de sous-groupes d’indice fini de $SL_2(\mathbb{Z}) $, et l’action extérieure induite (quitte à passer également à un sous-groupe overt de $Gal(\overline{\mathbb{Q}},\mathbb{Q}) $), on trouve essentiellement les groupes fondamentaux de toutes les courbes algébriques définis sur des corps de nombres $K $, et l’action extérieure de $Gal(\overline{K}/K) $ dessus.”

So, is there a noncommutative affine variety over $\mathbb{F}_1 $ of which the unique minimal integral model is the integral group algebra of the modular group $\mathbb{Z} \Gamma $ (with $\Gamma = PSL_2(\mathbb{Z}) $? Yes, here it is

$N_{\Gamma}~:~\mathbf{groups} \rightarrow \mathbf{sets} \qquad G \mapsto G_2 \times G_3 $

where $G_n $ is the set of all elements of order $n $ in $G $. The reason behind this is that the modular group is the free group product $C_2 \ast C_3 $.

Fine, you may say, but all this is just algebra. Where is the noncommutative complex variety or the noncommutative integral scheme in all this? Well, we can introduce them too but as this post is already 1300 words long, I’ll better leave this for another time. In case you cannot stop thinking about it, here’s the short answer.

The complex noncommutative variety has as its ‘points’ all finite dimensional simple complex representations of the modular group, and the ‘points’ of the noncommutative $\mathbb{F}_1 $-scheme are exactly the (modular) dessins d’enfants…