Tag: Mathieu

The M(13)-groupoid (2)

Published July 30, 2007 by lievenlb

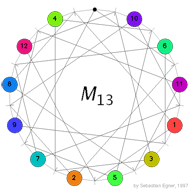
Conway’s puzzle M(13) involves the 13 points and 13 lines of $\mathbb{P}^2(\mathbb{F}_3) $. On all but one point numbered counters are placed holding the numbers 1,…,12 and a move involves interchanging one counter and the ‘hole’ (the unique point having no counter) and interchanging the counters on the two other points of the line determined by the first two points. In the picture on the left, the lines are respresented by dashes around the circle in between two counters and the points lying on this line are those that connect to the dash either via a direct line or directly via the circle. In the first part we saw that the group of all reachable positions in Conway’s M(13) puzzle having the hole at the top positions contains the sporadic simple Mathieu group $M_{12} $ as a subgroup. To see the reverse inclusion we have to recall the definition of the ternary Golay code named in honour of the Swiss engineer Marcel Golay who discovered in 1949 the binary Golay code that we will encounter _later on_.

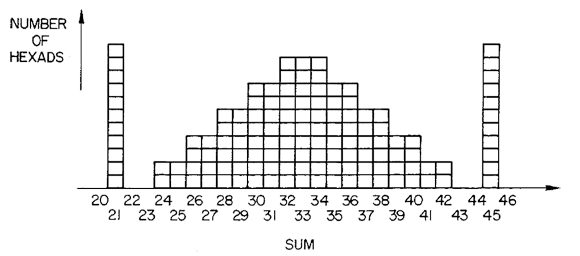
The ternary Golay code $\mathcal{C}_{12} $ is a six-dimenional subspace in $\mathbb{F}_3^{\oplus 12} $ and is spanned by its codewords of weight six (the Hamming distance of $\mathcal{C}_{12} $ whence it is a two-error correcting code). There are $264 = 2 \times 132 $ weight six codewords and they can be obtained from the 132 hexads, we encountered before as the winning positions of Mathieu’s blackjack, by replacing the stars by signs + or – using the following rules. By a tet (from tetracodeword) we mean a 3×4 array having 4 +-signs indicating the row-positions of a tetracodeword. For example

$~\begin{array}{|c|ccc|} \hline & + & & \\ + & & + & \\ & & & + \\ \hline + & 0 & + & – \end{array} $ is the tet corresponding to the bottom-tetracodeword. $\begin{array}{|c|ccc|} \hline & + & & \\ & + & & \\ & + & & \\ \hline & & & \end{array} $ A col is an array having +-signs along one of the four columns. The signed hexads will now be the hexads that can be written as $\mathbb{F}_3 $ vectors as (depending on the column-distributions of the stars in the hexad indicated between brackets)

$col-col~(3^20^2)\qquad \pm(col+tet)~(31^3) \qquad tet-tet~(2^30) \qquad \pm(col+col-tet)~(2^21^2) $

For example, the hexad on the right has column-distribution $2^30 $ so its signed versions are of the form tet-tet. The two tetracodewords must have the same digit (-) at place four (so that they cancel and leave an empty column). It is then easy to determine these two tetracodewords giving the signed hexad (together with its negative, obtained by replacing the order of the two codewords)

$\begin{array}{|c|ccc|} \hline \ast & \ast & & \\ \ast & & \ast & \\ & \ast & \ast & \\ \hline – & + & 0 & – \end{array} $ signed as
$\begin{array}{|c|ccc|} \hline + & & & \\ & & & \\ & + & + & + \\ \hline 0 & – & – & – \end{array} – \begin{array}{|c|ccc|} \hline & + & & \\ + & & + & \\ & & & + \\ \hline + & 0 & + & – \end{array} = \begin{array}{|c|ccc|} \hline + & – & & \\ – & & – & \\ & + & + & \\ \hline – & + & 0 & – \end{array} $

and similarly for the other cases. As Conway&Sloane remark ‘This is one of many cases when the process is easier performed than described’.

We have an order two operation mapping a signed hexad to its negative and as these codewords span the Golay code, this determines an order two automorphism of $\mathcal{C}_{12} $. Further, forgetting about signs, we get the Steiner-system S(5,6,12) of hexads for which the automorphism group is $M_{12} $ hence the automorphism group op the ternary Golay code is $2.M_{12} $, the unique nonsplit central extension of $M_{12} $.

Right, but what is the connection between the Golay code and Conway’s M(13)-puzzle which is played with points and lines in the projective plane $\mathbb{P}^2(\mathbb{F}_3) $? There are 13 points $\mathcal{P} $ so let us consider a 13-dimensional vectorspace $X=\mathbb{F}_3^{\oplus 13} $ with basis $x_p~:~p \in \mathcal{P} $. That is a vector in X is of the form $\vec{v}=\sum_p v_px_p $ and consider the ‘usual’ scalar product $\vec{v}.\vec{w} = \sum_p v_pw_p $ on X. Next, we bring in the lines in $\mathbb{P}^2(\mathbb{F}_3) $.

For each of the 13 lines l consider the vector $\vec{l} = \sum_{p \in l} x_p $ with support the four points lying on l and let $\mathcal{C} $ be the subspace (code) of X spanned by the thirteen vectors $\vec{l} $. Vectors $\vec{c},\vec{d} \in \mathcal{C} $ satisfy the remarkable identity $\vec{c}.\vec{d} = (\sum_p c_p)(\sum_p d_p) $. Indeed, both sides are bilinear in $\vec{c},\vec{d} $ so it suffices to check teh identity for two line-vectors $\vec{l},\vec{m} $. The right hand side is then 4.4=16=1 mod 3 which equals the left hand side as two lines either intersect in one point or are equal (and hence have 4 points in common). The identity applied to $\vec{c}=\vec{d} $ gives us (note that the squares in $\mathbb{F}_3 $ are {0,1}) information about the weight (that is, the number of non-zero digits) of codewords in $\mathcal{C} $

$wt(\vec{c})~mod(3) = \sum_p c_p^2 = (\sum_p c_p)^2 \in \{ 0,1 \} $

Let $\mathcal{C}’ $ be the collection of $\vec{c} \in \mathcal{C} $ of weight zero (modulo 3) then one can verify that $\mathcal{C}’ $ is the orthogonal complement of $\mathcal{C} $ with respect to the scalar product and that the dimension of $\mathcal{C} $ is seven whereas that of $\mathcal{C}’ $ is six.
Now, let for a point p be $\mathcal{G}_p $ the restriction of

$\mathcal{C}_p = \{ c \in \mathcal{C}~|~c_p = – \sum_{q \in \mathcal{P}} c_q \} $

to the coordinates of $\mathcal{P} – \{ p \} $, then $\mathcal{G}_p $ is clearly a six dimensional code in a 12-dimensional space. A bit more work shows that $\mathcal{G}_p $ is a self-dual code with minimal weight greater or equal to six, whence it must be the ternary Golay code! Now we are nearly done. _Next time_ we will introduce a reversi-version of M(13) and use the above facts to deduce that the basic group of the Mathieu-groupoid indeed is the sporadic simple group $M_{12} $.

References

Robert L. Griess, “Twelve sporadic groups” chp. 7 ‘The ternary Golay code and $2.M_{12} $’

John H. Conway and N. J.A. Sloane, “Sphere packings, lattices and groups” chp 11 ‘The Golay codes and the Mathieu groups’

John H. Conway, Noam D. Elkies and Jeremy L. Martin, ‘The Mathieu group $M_{12} $ and its pseudogroup extension $M_{13} $’ arXiv:math.GR/0508630

Mathieu’s blackjack (3)

Published July 17, 2007 by lievenlb

If you only tune in now, you might want to have a look at the definition of Mathieu’s blackjack and the first part of the proof of the Conway-Ryba winning strategy involving the Steiner system S(5,6,12) and the Mathieu sporadic group $M_{12} $.

We’re trying to disprove the existence of misfits, that is, of non-hexad positions having a total value of at least 21 such that every move to a hexad would increase the total value. So far, we succeeded in showing that such a misfit must have the patern

$\begin{array}{|c|ccc|} \hline 6 & III & \ast & 9 \\ 5 & II & 7 & . \\ IV & I & 8 & . \\ \hline & & & \end{array} $

That is, a misfit must contain the 0-card (queen) and cannot contain the 10 or 11(jack) and must contain 3 of the four Romans. Now we will see that a misfit also contains precisely one of {5,6} (and consequently also exactly one card from {7,8,9}). To start, it is clear that it cannot contain BOTH 5 and 6 (then its total value can be at most 20). So we have to disprove that a misfit can miss {5,6} entirely (and so the two remaining cards (apart from the zero and the three Romans) must all belong to {7,8,9}).

Lets assume the misfit misses 5 and 6 and does not contain 9. Then, it must contain 4 (otherwise, its column-distribution would be (0,3,3,0) and it would be a hexad). There are just three such positions possible

$\begin{array}{|c|ccc|} \hline . & \ast & \ast & . \\ . & \ast & \ast & . \\ \ast & . & \ast & . \\ \hline – & – & ? & ? \end{array} $ $\begin{array}{|c|ccc|} \hline . & \ast & \ast & . \\ . & . & \ast & . \\ \ast & \ast & \ast & . \\ \hline – & + & ? & ? \end{array} $ $\begin{array}{|c|ccc|} \hline . & . & \ast & . \\ . & \ast & \ast & . \\ \ast & \ast & \ast & . \\ \hline – & 0 & ? & ? \end{array} $

Neither of these can be misfits though. In the first one, there is an 8->5 move to a hexad of smaller total value (in the second a 7->5 move and in the third a 7->6 move). Right, so the 9 card must belong to a misfit. Assume it does not contain the 4-card, then part of the misfit looks like (with either a 7- or an 8-card added)

$\begin{array}{|c|ccc|} \hline . & \ast & \ast & \ast \\ . & \ast & ? & . \\ . & \ast & ? & . \\ \hline & & & \end{array} $ contained in the unique hexad $\begin{array}{|c|ccc|} \hline \ast & \ast & \ast & \ast \\ . & \ast & & . \\ . & \ast & & . \\ \hline & & & \end{array} $

Either way the moves 7->6 or 8->6 decrease the total value, so it cannot be a misfit. Therefore, a misfit must contain both the 4- and 9-card. So it is of the form on the left below

$\begin{array}{|c|ccc|} \hline . & ? & \ast & \ast \\ . & ? & ? & . \\ \ast & ? & ? & . \\ \hline & & & \end{array} $ $\begin{array}{|c|ccc|} \hline . & . & \ast & . \\ . & \ast & \ast & \ast \\ \ast & \ast & . & . \\ \hline – & 0 & – & + \end{array} $ $\begin{array}{|c|ccc|} \hline . & . & \ast & \ast \\ . & \ast & \ast & . \\ \ast & \ast & . & . \\ \hline & & & \end{array} $

If this is a genuine misfit only the move 9->10 to a hexad is possible (the move 9->11 is not possible as all BUT ONE of {0,1,2,3,4} is contained in the misfit). Now, the only hexad containing 0,4,10 and 2 from {1,2,3} is in the middle, giving us what the misfit must look like before the move, on the right. Finally, this cannot be a misfit as the move 7->5 decreases the total value.

That is, we have proved the claim that a misfit must contain one of {5,6} and one of {7,8,9}. Right, now we can deliver the elegant finishing line of the Kahane-Ryba proof. A misfit must contain 0 and three among {1,2,3,4} (let us call the missing card s), one of $5+\epsilon $ with $0 \leq \epsilon \leq 1 $ and one of $7+\delta $ with $0 \leq \delta \leq 2 $. Then, the total value of the misfit is

$~(0+1+2+3+4-s)+(5+\epsilon)+(7+\delta)=21+(1+\delta+\epsilon-s) $

So, if this value is strictly greater than 21 (and we will see in a moment is has to be if it is at least 21) then we deduce that $s < 1 + \delta + \epsilon \leq 4 $. Therefore $1+\delta+\epsilon $ belongs to the misfit. But then the move $1+\delta \epsilon \rightarrow s $ moves the misfit to a 6-tuple with total value 21 and hence (as we see in a moment) must be a hexad and hence this is a decreasing move! So, finally, there are no misfits!

Hence, from every non-hexad pile of total value at least 21 we have a legal move to a hexad. Because the other player cannot move from an hexad to another hexad we are done with our strategy provided we can show (a) that the total value of any hexad is at least 21 and (b) that ALL 6-piles of total value 21 are hexads. As there are only 132 hexads it is easy enough to have their sum-distribution. Here it is

That is, (a) is proved by inspection and we see that there are 11 hexads of sum 21 (the light hexads in Conway-speak) and there are only 11 ways to get 21 as a sum of 6 distinct numbers from {0,1,..,11} so (b) follows. Btw. the obvious symmetry of the sum-distribution is another consequence of the duality t->11-t discussed briefly at the end of part 2.

Clearly, I’d rather have conceptual proofs for all these facts and briefly tried my hand. Luckily I did spot the following phrase on page 326 of Conway-Sloane (discussing the above distribution) :

“It will not be easy to explain all the above observations. They are certainly connected with hyperbolic geometry and with the ‘hole’ structure of the Leech lattice.”

So, I’d better leave it at this…

References

Joseph Kahane and Alexander J. Ryba, “The hexad game“

John H. Conway and N. J.A. Sloane, “Sphere packings, Lattices and Groups” chp. 11 ‘The Golay codes and the Mathieu groups’

Mathieu’s blackjack (2)

Published July 17, 2007 by lievenlb

(continued from part one). Take twelve cards and give them values 0,1,2,…,11 (for example, take the jack to have value 11 and the queen to have value 0). The hexads are 6-tuples of cards having the following properties. When we star their values by the scheme on the left below and write a 0 below a column if it has just one star at the first row or two stars on rows two and three (a + if the unique star is at the first row or two stars in the other columns, and a – if the unique star in on the second row or two stars in rows one and two) or a ? if the column has 3 or 0 stars, we get a tetracodeword where we are allowed to replace a ? by any digit. Moreover, we want that the stars are NOT distributed over the four columns such that all of the possible outcomes 0,1,2,3 appear once. For example, the card-pile { queen, 3, 4, 7, 9, jack } is an hexad as is indicated on the right below and has column-distributions (1,1,2,2).

$\begin{array}{|c|ccc|} \hline 6 & 3 & 0 & 9 \\ 5 & 2 & 7 & 10 \\ 4 & 1 & 8 & 11 \\ \hline & & & \end{array} $ $\begin{array}{|c|ccc|} \hline & \ast & \ast & \ast \\ & & \ast & \\ \ast & & & \ast \\ \hline – & 0 & – & + \end{array} $

The hexads form a Steiner-system S(5,6,12), meaning that every 5-pile of cards is part of a unique hexad. The permutations on these twelve cards, having the property that they send every hexad to another hexad, form the sporadic simple group $M_{12} $, the _Mathieu group_ of order 95040. For now, we assume these facts and deduce from them the Conway-Ryba winning strategy for Mathieu’s blackjack : the hexads are exactly the winning positions and from a non-hexad pile of total value at least 21 there is always a legal (that is, total value decreasing) move to an hexad by replacing one card in the pile by a card from the complement.

It seems that the first proof of this strategy consisted in calculating the Grundy values of all 905 legal positions in Mathieu’s blackjack. Later Joseph Kahane and Alex Ryba gave a more conceptual proof, that we will try to understand.

Take a non-hexad 6-pile such that the total value of its cards is at least 21, then removing any one of the six cards gives a 5-pile and is by the Steiner-property contained in a unique hexad. Hence we get 6 different hexads replacing one card from the non-hexad pile by a card not contained in it. We claim that at least one of these operations is a legal move, meaning that the total value of the cards decreases. Let us call a counterexample a misfit and record some of its properties until we can prove its non-existence.

A misfit is a non-hexad with total value at least 21 such that all 6 hexads, obtained from it by replacing one card by a card from its complement, have greater total value

A misfit must contain the queen-card. If not, we could get an hexad replacing one misfit-card (value > 0) by the queen (value zero) so this would be a legal move. Further, the misfit cannot contain the jack-card for otherwise replacing it by a lower-valued card to obtain an hexad is a legal move.

A misfit contains at least three cards from {queen,1,2,3,4}. If not, three of these cards are the replacements of misfit-cards to get an hexad, but then at least one of the replaced cards has a greater value than the replacement, giving a legal move to an hexad.

A misfit contains more than three cards from {queen=0, 1,2,3,4}. Assume there are precisely three $\{ c_1,c_2,c_3 \} $ from this set, then the complement of the misfit in the hexad {queen,1,2,3,4,jack} consists of three elements $\{ d_1,d_2,d_3 \} $ (a misfit cannot contain the jack). The two leftmost columns of the value-scheme (left above) form the hexad {1,2,3,4,5,6} and because the Mathieu group acts 5-transitively there is an element of $M_{12} $ taking $\{ 0,1,2,3,4,11 \} \rightarrow \{ 1,2,3,4,5,6 \} $ and we may even assume that it takes $\{ c_1,c_2,c_3 \} \rightarrow \{ 4,5,6 \} $. But then, in the new value-scheme (determined by that $M_{12} $-element) the two leftmost columns of the misfit look like

$\begin{array}{|c|ccc|} \hline \ast & . & ? & ? \\ \ast & . & ? & ? \\ \ast & . & ? & ? \\ \hline ? & ? & & \end{array} $

and the column-distribution of the misfit must be either (3,0,2,1) or (3,0,1,2) (it cannot be (3,0,3,0) or (3,0,0,3) otherwise the (image of the) misfit would be an hexad). Let {i,j} be the two misfit-values in the 2-starred column. Replacing either of them to get an hexad must have the replacement lying in the second column (in order to get a valid column distribution (3,1,1,1)). Now, the second column consists of two small values (from {0,1,2,3,4}) and the large jack-value (11). So, at least one of {i,j} is replaced by a smaller valued card to get an hexad, which cannot happen by the misfit-property.

Now, if the misfit shares four cards with {queen,1,2,3,4} then it cannot contain the 10-card. Otherwise, the replacement to get an hexad of the 10-card must be the 11-card (by the misfit-property) but then there would be another hexads containing five cards from {queen,0,1,2,3,jack} which cannot happen by the Steiner-property. Right, let’s summarize what we know so far about our misfit. Its value-scheme looks like

$\begin{array}{|c|ccc|} \hline 6 & III & \ast & 9 \\ 5 & II & 7 & . \\ IV & I & 8 & . \\ \hline & & & \end{array} $ and it must contain three of the four Romans. At this point Kahane and Ryba claim that the two remaining cards (apart from the queen and the three romans) must be such that there is exactly one from {5,6} and exactly one from {7,8,9}. They argue this follows from duality where the dual pile of a card-pile $\{ x_1,x_2,\ldots,x_6 \} $ is the pile $\{ 11-x_1,11-x_2,\ldots,11-x_6 \} $. This duality acts on the hexads as the permutation $~(0,11)(1,10)(2,9)(3,8)(4,7)(5,6) \in M_{12} $. Still, it is unclear to me how they deduce from it the above claim (lines 13-15 of page 4 of their paper). I’d better have some coffee and work around this (to be continued…)

If you want to play around a bit with hexads and the blackjack game, you’d better first download SAGE (if you haven’t done so already) and then get David Joyner’s hexad.sage file and put it in a folder under your sage installation (David suggests ‘spam’ himself…). You can load the routines into sage by typing from the sage-prompt attach ‘spam/hexad.sage’. Now, you can find the hexad from a 5-pile via the command find_hexad([a1,a2,a3,a4,a5],minimog_shuffle) and you can get the winning move for a blackjack-position via blackjack_move([a1,a2,a3,a4,a5,a6],minimog_shuffle). More details are in the Joyner-Casey(Luers) paper referenced last time.

Reference

Joseph Kahane and Alexander J. Ryba, ‘The hexad game‘