Skip to content →

Tag: mac

From WordPress to ePublishing (1)

Published July 11, 2011 by lievenlb

Perhaps, the tips and tricks I did receive to turn a selection of wordpress-posts into a proper ePub-file may be of use to others, so I will describe the procedure here in some detail.

It makes a difference whether or not some of the posts contain TeX. This time, I’ll sketch the process for non-LaTeX posts and hence we will turn the Bourbaki-code posts into ePub-format to read on your iPad, rather than merely into a pdf-file as last time. Next time, I’ll add some tricks to repeat this when some of your posts do contain LaTeX.

1. Install the ePub export plugin

Get the epub export wordpress plugin, install and activate it in the usual way. ePub Export automatically creates an ePub file when a post or page is published or updated. The ePubs are stored in the uploads directory. For later use, remember that your uploads directories are located under BLOGHOME/wp-content/uploads.

2. Update the posts you want to include

Decide which posts you want to include in your eBook, edit them (or not) and press for each one of them the update-button. This will populate today’s uploads-directory with a number of epub-files. Transfer them all, for example using Transmit, to a directory on your home-computer, named say MyFirstEBook.



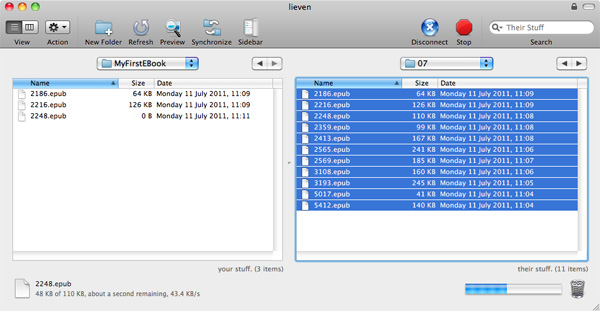
3. Unpack the epub-files

The crucial fact to remember about epub-files is that they are really zipped archives containing xhtml-, css- and other files and directories. As we want to edit some of those, we first have to unpack the directories. So, change the .epub extensions to .zip and double-click on them to create the directories.



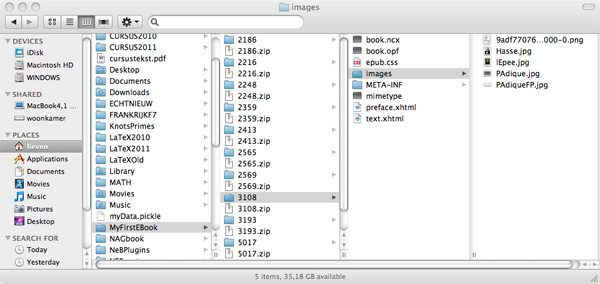
The crucial files in each directory are preface.xhtml (containing title author and blog-name), text.html (containing the blog-post) and the images-directory (containing copies of all the images used in the post).

4. Rename the directories user-friendly

As all the posts will be chapters in our eBook in some specific order, we will rename the numbers of the directories to something more user-friendly such as shortened blog-titles. To do this, double-click in each of the directories on the preface.xhtml file. This will open Safari and will show the title of the blog-post. Use it to rename that directory. For convenience let us call the directory corresponding to the first chapter in our book MasterDirectory

5. Move all images to the master directory

For each of the other chapter-directories, drag all the files contained in the images-subdirectory to MasterDirectory/images.

6. Edit the MasterDirectory/text.xhtml file

Because we will have to open and copy-paste all the text.xhtml files of the different directories, it is perhaps best to rename momentarily the MasterDirectory/text.xhtml file to something like master.xhtml.

Now, open this file with a text-processor such as TextWrangler. Edit it to remove unwanted html-code (such as links to other posts at the start if you are using the series-plugin, or previous/next post links at the end). Also add the title of the blog-post between h1-tags (and if you want to include a table of contents later, give it an anchor-name).

Go to the directory of your second chapter, open that text.xhtml file and copy/paste only the post-content over to the master-xhtml file at the appropriate place. As before, add title/anchor before the copied post-content.

Repeat this procedure, in order, for all the chapters of your eBook.

Once finished, doubleclick the master.xhtml file and correct remaining errors (as it is an xhtml-file, it is rather picky about opening and closing tags) and see whether all your images are included. If you’re satisfied with it, rename the master.xhtml to text.xhtml (don’t forget this!).

7. Edit the MasterDirectory/preface.xhtml file

Open the preface.xhtml file and change the first blogpost-title to the title of your booklet, alter your name (by default it uses your wp-nick) and add a frontipiece-picture if you so desire.

8. Re-package the directory into an epub-file

This is the (only) tricky part. E-book readers require that the mimetype file is the first one in the zip document. What’s more, to be fully compliant, this file should start at a very specific point – a 30-byte offset from the beginning of the zip file (so that the mimetype text itself starts at byte 38).

Here’s how to do this on a Mac (Linux-users being the geeks they are will have given up on reading this post a while ago and as to Windows-users, yeah well …). Open Terminal.app and cd to your MasterDirectory. Now type:

zip -X MyFirstEBook.epub mimetype

Next, type:

zip -rg MyFirstEBook.epub * -x *.DS_Store

(of course you’ll have to change your book-title to whatever you want). If you want to know more about these 2 magical commands, read this post.

9. Edit metadata

Get Calibre and add the MyFirstEBook.epub to Calibre by clicking on the ‘Add Books’ button.



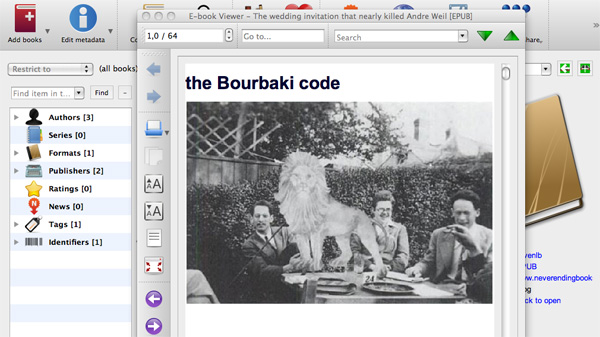
You can preview your eBook by clicking on the ‘View’-button. Next, click the ‘Edit metadata’-button and alter the title and author entries (and whatever else you want to include) and click the OK button. Then click ‘Save to disk’.

10. Read your eBook on your iPad

Finally, we want to see how it looks on the iPad. Mail MyFirstEBook.epub to yourself as attachement, open it with iBooks and enjoy!

Leave a Comment

What’s Pippa got to do with the Bourbaki wedding?

Published July 9, 2011 by lievenlb

Last time we’ve seen that on June 3rd 1939, the very day of the Bourbaki wedding, Malraux’ movie ‘L’espoir’ had its first (private) viewing, and we mused whether Weil’s wedding card was a coded invitation to that event.

But, there’s another plausible explanation why the Bourbaki wedding might have been scheduled for June 3rd : it was intended to be a copy-cat Royal Wedding…

The media-hype surrounding the wedding of Prince William to Pippa’s sister led to a hausse in newspaper articles on iconic royal weddings of the past.

One of these, the marriage of Edward VIII, Duke of Windsor and Wallis Warfield Spencer Simpson, was held on June 3rd 1937 : “This was the scandal of the century, as far as royal weddings go. Edward VIII had just abdicated six months before in order to marry an American twice-divorced commoner. The British Establishment at the time would not allow Edward VIII to stay on the throne and marry this woman (the British Monarch is also the head of the Church of England), so Edward chose love over duty and fled to France to await the finalization of his beloved’s divorce. They were married in a private, civil ceremony, which the Royal Family boycotted.”

But, what does this wedding have to do with Bourbaki?

For starters, remember that the wedding-card-canular was concocted in the spring of 1939 in Cambridge, England. So, if Weil and his Anglo-American associates needed a common wedding-example, the Edward-Wallis case surely would spring to mind. One might even wonder about the transposed symmetry : a Royal (Betti, whose father is from the Royal Poldavian Academy), marrying an American (Stanislas Pondiczery).

Even Andre Weil must have watched this wedding with interest (perhaps even sympathy). He too had to wait a considerable amount of time for Eveline’s divorce (see this post) to finalize, so that they could marry on october 30th 1937, just a few months after Edward & Wallis.



But, there’s more. The royal wedding took place at the Chateau de Cande, just south of Tours (the A on the google-map below). Now, remember that the 2nd Bourbaki congress was held at the Chevalley family-property in Chancay (see the Escorial post) a bit to the north-east of Tours (the marker on the map). As this conference took place only a month after the Royal Wedding (from 10th till 20th of July 1937), the event surely must have been the talk of the town.

Early on, we concluded that the Bourbaki-Petard wedding took place at 12 o’clock (‘a l’heure habituelle’). So did the Edward-Wallis wedding. More precisely, the civil ceremony began at 11.47 and the local mayor had to come to the castle for the occasion, and, afterwards the couple went into the music-room, which was converted into an Anglican chapel for the day, at precisely 12 o’clock.

The emphasis on the musical organ in the Bourbaki wedding-invitation allowed us to identify the identity of ‘Monsieur Modulo’ to be Olivier Messiaen as well as that of the wedding church. Now, the Chateau de Cande also houses an impressive organ, the Skinner opus 718 organ.

For the wedding ceremony, Edward and Wallis hired the services of one of the most renowned French organists at the time : Marcel Dupre who was since 1906 Widor’s assistent, and, from 1934 resident organist in the Saint-Sulpice church in Paris. Perhaps more telling for our story is that Dupre was, apart from Paul Dukas, the most influential teacher of Olivier Messiaen.

On June 3rd, 1937 Dupre performed the following pieces. During the civil ceremony, an extract from the 29e Bach cantate, canon in re-minor by Schumann and the prelude of the fugue in do-minor of himself. When the couple entered the music room he played the march of the Judas Macchabee oratorium of Handel and the cortege by himself. During the religious ceremony he performed his own choral, adagium in mi-minor by Cesar Franck, the traditional ‘Oh Perfect Love’, the Jesus-choral by Bach and the toccata of the 5th symphony of Widor. Compare this level of detail to the minimal musical hint given in the Bourbaki wedding-invitation

“Assistent Simplexe de la Grassmannienne (lemmas chantees par la Scholia Cartanorum)”

This is one of the easier riddles to solve. The ‘simplicial assistent of the Grassmannian’ is of course Hermann Schubert (Schubert cell-decomposition of Grassmannians). But, the composer Franz Schubert only left us one organ-composition : the Fugue in E-minor.

I have tried hard to get hold of a copy of the official invitation for the Edward-Wallis wedding, but failed miserably. There must be quite a few of them still out there, of the 300 invited people only 16 showed up… You can watch a video newsreel film of the wedding.

As Claude Chevalley’s father had an impressive diplomatic career behind him and lived in the neighborhood, he might have been invited, and, perhaps the (unused) invitation was lying around at the time of the second Bourbaki-congress in Chancay,just one month after the Edward-Wallis wedding…

Leave a Comment

NeB : 7 years and now an iPad App

Published December 31, 2010 by lievenlb

Exactly 7 years ago I wrote my first post. This blog wasn’t called NeB yet and it used pMachine, a then free blogging tool (later transformed into expression engine), rather than WordPress.

Over the years NeB survived three hardware-upgrades of ‘the Matrix’ (the webserver hosting it), more themes than I care to remember, and a couple of dramatic closure announcements…

But then we’re still here, soldiering on, still uncertain whether there’s a point to it, but grateful for tiny tokens of appreciation.

Such as this morning’s story: Chandan deemed it necessary to correct two spelling mistakes in a 2 year old Fun-math post on Weil and the Riemann hypothesis (also reposted on Neb here). Often there’s a story behind such sudden comments, and a quick check of MathOverflow revealed this answer and the comments following it.

I thank Ed Dean for linking to the Fun-post, Chandan for correcting the misspellings and Georges for the kind words. I agree with Georges that a cut&copy of a blogpost-quoted text does not require a link to that post (though it is always much appreciated). It is rewarding to see such old posts getting a second chance…

Above the Google Analytics graph of the visitors coming here via a mobile device (at most 5 on a good day…). Anticipating much more iPads around after tonights presents-session I’ve made NeB more accessible for iPods, iPhones, iPads and other mobile devices.

The first time you get here via your Mac-device of choice you’ll be given the option of saving NeB as an App. It has its own icon (lowest row middle, also the favicon of NeB) and flashy start-up screen.

Of course, the whole point trying to make NeB more readable for Mobile users you get an overview of the latest posts together with links to categories and tags and the number of comments. Sliding through you can read the post, optimized for the device.

I do hope you will use the two buttons at the end of each post, the first to share or save it and the second to leave a comment.

I wish you all a lot of mathematical (and other) fun in 2011 :: lieven.

3 Comments