Nimbers is a 2-person game, winnable only if you understand the arithmetic of the finite fields $\mathbb{F}_{2^{2^n}} $ associated to Fermat 2-powers.
It is played on a rectangular array (say a portion of a Go-board, for practical purposes) having a finite number of stones at distinct intersections. Here’s a typical position
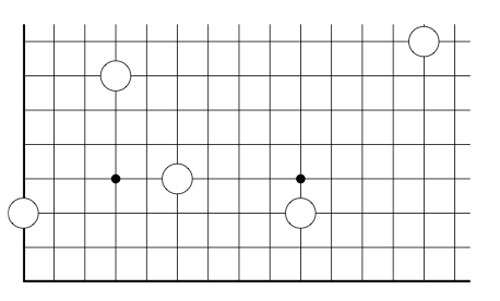
The players alternate making a move, which is either
- removing one stone, or
- moving a stone to a spot on the same row (resp. the same column) strictly to the left (resp. strictly lower), and if there’s already a stone on this spot, both stones are removed, or
- adding stones to the empty corners of a rectangle having as its top-right hand corner a chosen stone and removing stones at the occupied corners
Here we illustrate two possible moves from the above position, in the first we add two new stones and remove 2 existing stones, in the second we add three new stones and remove only the top right-hand stone.
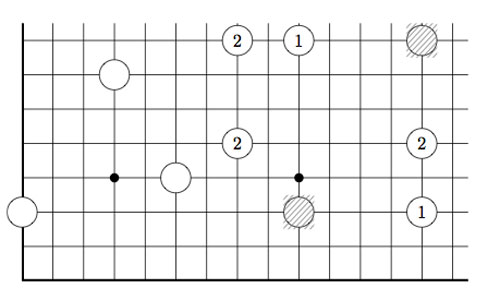
As always, the last player able to move wins the game!
Note that Nimbers is equivalent to Lenstra’s ‘turning corners’-game (as introduced in his paper Nim-multiplication or mentioned in Winning Ways Chapter 14, page 473).
If all stones are placed on the left-most column (or on the bottom row) one quickly realizes that this game reduces to classical Nim with Nim-heap sizes corresponding to the stones (for example, the left-most stone corresponds to a heap of size 3).
Nim-addition $n \oplus m $ is defined inductively by
$n \oplus m = mex(n’ \oplus m,n \oplus m’) $
where $n’ $ is any element of ${ 0,1,\ldots,n-1 } $ and $m’ $ any element of ${ 0,1,\ldots,m-1 } $ and where ‘mex’ stands for Minimal EXcluded number, that is the smallest natural number which isn’t included in the set. Alternatively, one can compute $n \oplus m $ buy writing $n $ and $m $ in binary and add these binary numbers without carrying-over. It is well known that a winning strategy for Nim tries to shorten one Nim-heap such that the Nim-addition of the heap-sizes equals zero.
This allows us to play Nimber-endgames, that is, when all the stones have been moved to the left-column or the bottom row.
To evaluate general Nimber-positions it is best to add another row and column, the coordinate axes of the array
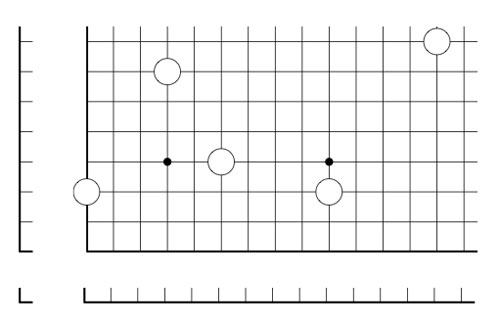
and so our stones lie at positions (1,3), (4,7), (6,4), (10,3) and (14,8). In this way all legal moves follow the rectangle-rule when we allow rectangles to contain corners on the added coordinate axes. For example, removing a stone is achieved by taking a rectangle with two sides on the added axes, and, moving a stone to the left (or the bottom) is done by taking a rectangle with one side at the x-axes (resp. the y-axes)
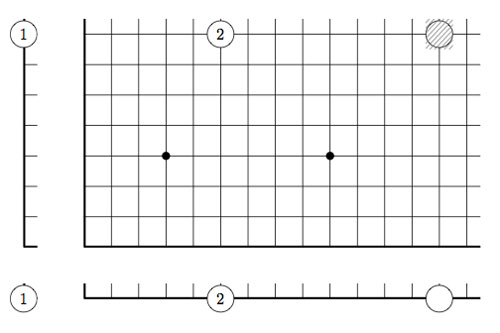
However, the added stones on the coordinate axes are considered dead and may be removed from the game. This observation allows us to compute the Grundy number of a stone at position (m,n) to be
$G(m,n)=mex(G(m’,n’) \oplus G(m’,n) \oplus G(m,n’)~:~0 \leq m’ < m, 0 \leq n’ < n) $
and so by induction these Grundy numbers are equal to the Nim-multiplication $G(m,n) = m \otimes n $ where
$m \otimes n = mex(m’ \otimes n’ \oplus m’ \otimes n \oplus m \otimes n’~:~0 \leq m’ < m, 0 \leq n’ < n) $
Thus, we can evaluate any Nimbers-position with stone-coordinates smaller than $2^{2^n} $ by calculating in a finite field using the identification (as for example in the odd Knights of the round table-post) $\mathbb{F}_{2^{2^n}} = \{ 0,1,2,\ldots,2^{2^n}-1 \} $
For example, when all stones lie in a 15×15 grid (as in the example above), all calculations can be performed using
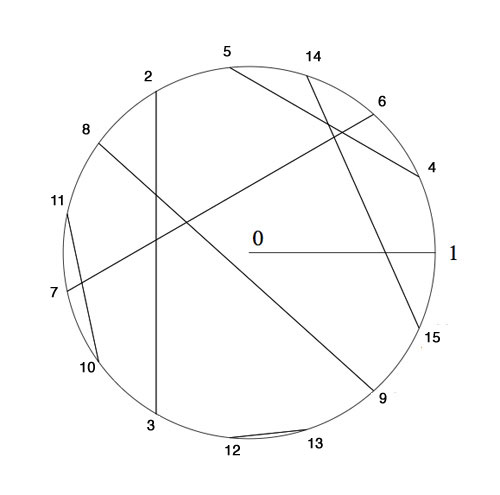
Here, we’ve identified the non-zero elements of $\mathbb{F}_{16} $ with 15-th roots of unity, allowing us to multiply, and we’ve paired up couples $(n,n \oplus 1) $ allowing u to reduce nim-addition to nim-multiplication via
$n \oplus m = (n \otimes \frac{1}{m}) \otimes (m \oplus 1) $
In particular, the stone at position (14,8) is equivalent to a Nim-heap of size $14 \otimes 8=10 $. The nim-value of the original position is equal to 8

Suppose your opponent lets you add one extra stone along the diagonal if you allow her to start the game, where would you have to place it and be certain you will win the game?








 In 1956,
In 1956,