Tag: Leech

a monstrous unimodular lattice

Published April 30, 2021 by lievenlb

An integral $n$-dimensional lattice $L$ is the set of all integral linear combinations
\[
L = \mathbb{Z} \lambda_1 \oplus \dots \oplus \mathbb{Z} \lambda_n \]
of base vectors $\{ \lambda_1,\dots,\lambda_n \}$ of $\mathbb{R}^n$, equipped with the usual (positive definite) inner product, satisfying
\[
(\lambda, \mu ) \in \mathbb{Z} \quad \text{for all $\lambda,\mu \in \mathbb{Z}$.} \]
But then, $L$ is contained in its dual lattice $L^* = Hom_{\mathbb{Z}}(L,\mathbb{Z})$, and if $L = L^*$ we say that $L$ is unimodular.

If all $(\lambda,\lambda) \in 2 \mathbb{Z}$, we say that $L$ is an even lattice. Even unimodular lattices (such as the $E_8$-lattice or the $24$ Niemeier lattices) are wonderful objects, but they can only live in dimensions $n$ which are multiples of $8$.

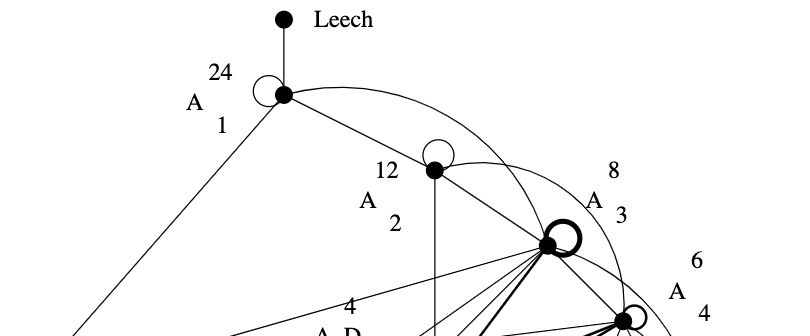
Just like the Conway group $Co_0 = .0$ is the group of rotations of the Leech lattice $\Lambda$, one might ask whether there is a very special lattice on which the Monster group $\mathbb{M}$ acts faithfully by rotations. If such a lattice exists, it must live in dimension at least $196883$.

Simon Norton (1952-2019) – Photo Credit

A first hint of such a lattice is in Conway’s original paper A simple construction for the Fischer-Griess monster group (but not in the corresponding chapter 29 of SPLAG).

Conway writes that Simon Norton showed ‘by a very simple computations that does not even require knowledge of the conjugacy classes, that any $198883$-dimensional representation of the Monster must support an invariant algebra’, which, after adding an identity element $1$, we now know as the $196884$-dimensional Griess algebra.

Further, on page 529, Conway writes:

Norton has shown that the lattice $L$ spanned by vectors of the form $1,t,t \ast t’$, where $t$ and $t’$ are transposition vectors, is closed under the algebra multiplication and integral with respect to the doubled inner product $2(u,v)$. The dual quotient $L^*/L$ is cyclic of order some power of $4$, and we believe that in fact $L$ is unimodular.

Here, transposition vectors correspond to transpositions in $\mathbb{M}$, that is, elements of conjugacy class $2A$.

I only learned about this lattice yesterday via the MathOverflow-post A lattice with Monster group symmetries by Adam P. Goucher.

In his post, Adam considers the $196883$-dimensional lattice $L’ = L \cap 1^{\perp}$ (which has $\mathbb{M}$ as its rotation symmetry group), and asks for the minimal norm (squared) of a lattice point, which he believes is $448$, and for the number of minimal vectors in the lattice, which might be
\[
2639459181687194563957260000000 = 9723946114200918600 \times 27143910000 \]
the number of oriented arcs in the Monster graph.

Here, the Monster graph has as its vertices the elements of $\mathbb{M}$ in conjugacy class $2A$ (which has $9723946114200918600$ elements) and with an edge between two vertices if their product in $\mathbb{M}$ again belongs to class $2A$, so the valency of the graph must be $27143910000$, as explained in that old post the monster graph and McKay’s observation.

When I asked Adam whether he had more information about his lattice, he kindly informed me that Borcherds told him that the Norton lattice $L$ didn’t turn out to be unimodular after all, but that a unimodular lattice with monstrous symmetry had been constructed by Scott Carnahan in the paper A Self-Dual Integral Form of the Moonshine Module.

Scott Carnahan – Photo Credit

The major steps (or better, the little bit of it I could grasp in this short time) in the construction of this unimodular $196884$-dimensional monstrous lattice might put a smile on your face if you are an affine scheme aficionado.

Already in his paper Vertex algebras, Kac-Moody algebras, and the Monster, Richard Borcherds described an integral form of any lattice vertex algebra. We’ll be interested in the lattice vertex algebra $V_{\Lambda}$ constructed from the Leech lattice $\Lambda$ and call its integral form $(V_{\Lambda})_{\mathbb{Z}}$.

One constructs the Moonshine module $V^{\sharp}$ from $V_{\Lambda}$ by a process called ‘cyclic orbifolding’, a generalisation of the original construction by Frenkel, Lepowsky and Meurman. In fact, there are now no less than 51 constructions of the moonshine module.

One starts with a fixed point free rotation $r_p$ of $\Lambda$ in $Co_0$ of prime order $p \in \{ 2,3,5,7,13 \}$, which one can lift to an automorphism $g_p$ of the vertex algebra $V_{\Lambda}$ of order $p$ giving an isomorphism $V_{\Lambda}/g_p \simeq V^{\sharp}$ of vertex operator algebras over $\mathbb{C}$.

For two distinct primes $p,p’ \in \{ 2,3,5,7,13 \}$ if $Co_0$ has an element of order $p.p’$ one can find one such $r_{pp’}$ such that $r_{pp’}^p=r_{p’}$ and $r_{pp’}^{p’}=r_p$, and one can lift $r_{pp’}$ to an automorphism $g_{pp’}$ of $V_{\Lambda}$ such that $V_{\Lambda}/g_{pp’} \simeq V_{\Lambda}$ as vertex operator algebras over $\mathbb{C}$.

Problem is that these lifts of automorphisms and the isomorphisms are not compatible with the integral form $(V_{\Lambda})_{\mathbb{Z}}$ of $V_{\Lambda}$, but ‘essentially’, they can be performed on
\[
(V_{\Lambda})_{\mathbb{Z}} \otimes_{\mathbb{Z}} \mathbb{Z}[\frac{1}{pp’},\zeta_{2pp’}] \]
where $\zeta_{2pp’}$ is a primitive $2pp’$-th root of unity. These then give a $\mathbb{Z}[\tfrac{1}{pp’},\zeta_{2pp’}]$-form on $V^{\sharp}$.

Next, one uses a lot of subgroup information about $\mathbb{M}$ to prove that these $\mathbb{Z}[\tfrac{1}{pp’},\zeta_{2pp’}]$-forms of $V^{\sharp}$ have $\mathbb{M}$ as their automorphism group.

Then, using all his for different triples in $\{ 2,3,5,7,13 \}$ one can glue and use faithfully flat descent to get an integral form $V^{\sharp}_{\mathbb{Z}}$ of the moonshine module with monstrous symmetry and such that the inner product on $V^{\sharp}_{\mathbb{Z}}$ is positive definite.

Finally, one looks at the weight $2$ subspace of $V^{\sharp}_{\mathbb{Z}}$ which gives us ~~our~~ Carnahan’s $196884$-dimensional unimodular lattice with monstrous symmetry!

Beautiful as this is, I guess it will be a heck of a project to deduce even the simplest of facts about this wonderful lattice from running through this construction.

For example, what is the minimal length of vectors? What is the number of minimal length vectors? And so on. All info you might have is very welcome.

One Comment

Know thy neighbours

Published March 24, 2021 by lievenlb

Two lattices $L$ and $L’$ in the same vector space are called neighbours if their intersection $L \cap L’$ is of index two in both $L$ and $L’$.

In 1957, Martin Kneser gave a method to find all unimodular lattices (of the same dimension and signature) starting from one such unimodular lattice, finding all its neighbours, and repeating this with the new lattices obtained.

In other words, Kneser’s neighbourhood graph, with vertices the unimodular lattices (of fixed dimension and signature) and edges between them whenever the lattices are neighbours, is connected.

Martin Kneser (1928-2004) – Photo Credit

Last time, we’ve constructed the Niemeier lattice $(A_1^{24})^+$ from the binary Golay code $\mathcal{C}_{24}$
\[
L = (A_1^{24})^+ = \mathcal{C}_{24} \underset{\mathbb{F}_2}{\times} (A_1^{24})^* = \{ \tfrac{1}{\sqrt{2}} \vec{v} ~|~\vec{v} \in \mathbb{Z}^{\oplus 24},~v=\vec{v}~mod~2 \in \mathcal{C}_{24} \} \]
With hindsight, we know that $(A_1^{24})^+$ is the unique neighbour of the Leech lattice in the Kneser neighbourhood graph of the positive definite, even unimodular $24$-dimensional lattices, aka the Niemeier lattices.

Let’s try to construct the Leech lattice $\Lambda$ from $L=(A_1^{24})^+$ by Kneser’s neighbour-finding trick.

Sublattices of $L$ of index two are in one-to-one correspondence with non-zero elements in $L/2L$. Take $l \in L – 2L$ and $m \in L$ such that the inner product $l.m$ is odd, then
\[
L_l = \{ x \in L~|~l.x~\text{is even} \} \]
is an index two sublattice because $L = L_l \sqcup (L_l+m)$. By definition $l.x$ is even for all $x \in L_l$ and therefore $\frac{l}{2} \in L_l^*$. We have this situation
\[
L_l \subsetneq L = L^* \subsetneq L_l^* \]
and $L_l^*/L_l \simeq \mathbb{F}_2 \oplus \mathbb{F}_2$, with the non-zero elements represented by $\{ \frac{l}{2}, m, \frac{l}{2}+m \}$. That is,
\[
L_l^* = L_l \sqcup (L_l+m) \sqcup (L_l+\frac{l}{2}) \sqcup (L_l+(\frac{l}{2}+m)) \]
This gives us three lattices
\[
\begin{cases}
M_1 &= L_l \sqcup (L_l+m) = L \\
M_2 &= L_l \sqcup (L_l+\frac{l}{2}) \\
M_3 &= L_l \sqcup (L_l+(\frac{l}{2}+m))
\end{cases}
\]
and all three of them are unimodular because
\[
L_l \subsetneq M_i \subseteq M_i^* \subsetneq L_l^* \]
and $L_l$ is of index $4$ in $L_l^*$.

Now, let’s assume the norm of $l$, that is, $l.l \in 4 \mathbb{Z}$. Then, either the norm of $\frac{l}{2}$ is odd (but then the norm of $\frac{l}{2}+m$ must be even), or the norm of $\frac{l}{2}$ is even, in which case the norm of $\frac{l}{2}+m$ is odd.

That is, either $M_2$ or $M_3$ is an even unimodular lattice, the other one being an odd unimodular lattice.

Let’s take for $l$ and $m$ the vectors $\lambda = \frac{1}{\sqrt{2}} (1,1,\dots,1) \in L – 2L$ and $\mu = \sqrt{2}(1,0,\dots,0) \in L$, then
\[
\lambda.\lambda = \frac{1}{2}\times 24 = 12 \quad \text{and} \quad \mu.\lambda = 1 \]
Because $\frac{\lambda}{2}.\frac{\lambda}{2} = \frac{12}{4}=3$ is odd, we have that
\[
\Lambda = L_{\lambda} \sqcup (L_{\lambda} + (\frac{\lambda}{2} + \mu)) \]
is an even unimodular lattice, which is the Leech lattice, and
\[
\Lambda_{odd} = L_{\lambda} \sqcup (L_{\lambda} + \frac{\lambda}{2}) \]
is an odd unimodular lattice, called the odd Leech lattice.

John Leech (1926-1992) – Photo Credit

Let’s check that these are indeed the Leech lattices, meaning that they do not contain roots (vectors of norm two).

The only roots in $L = (A_1^{24})^+$ are the $48$ roots of $A_1^{24}$ and they are of the form $\pm \sqrt{2} [ 1, 0^{23} ]$, but none of them lies in $L_{\lambda}$ as their inproduct with $\lambda$ is one. So, all non-zero vectors in $L_{\lambda}$ have norm $\geq 4$.

As for the other part of $\Lambda$ and $\Lambda_{odd}$
\[
(L_{\lambda} + \frac{\lambda}{2}) \sqcup (L_{\lambda} + \mu + \frac{\lambda}{2}) = (L_{\lambda} \sqcup (L_{\lambda}+\mu))+\frac{\lambda}{2} = L + \frac{\lambda}{2} \]
From the description of $L=(A_1^{24})^+$ it follows that every coordinate of a vector in $L + \frac{\lambda}{2}$ is of the form
\[
\frac{1}{\sqrt{2}}(v+\frac{1}{2}) \quad \text{or} \quad \frac{1}{\sqrt{2}}(v+\frac{3}{2}) \]
with $v \in 2 \mathbb{Z}$, with the second case instances forming a codeword in $\mathcal{C}_{24}$. In either case, the square of each of the $24$ coordinates is $\geq \frac{1}{8}$, so the norm of such a vector must be $\geq 3$, showing that there are no roots in this region either.

If one takes for $l$ a vector of the form $\frac{1}{\sqrt{2}} v = \frac{1}{\sqrt{2}}[1^a,0^{24-a}]$ where $a=8,12$ or $16$ and $v \in \mathcal{C}_{24}$, takes $m=\mu$ as before, and repeats the construction, one gets the other Niemeier-neighbours of $(A_1^{24})^+$, that is, the lattices $(A_2^{12})^+$, $(A_3^8)^+$ and $(D_4^6)^+$.

For $a=12$ one needs a slightly different argument, see section 0.2 of Richard Borcherds’ Ph.D. thesis.

The Leech lattice neighbour

Published March 23, 2021 by lievenlb

Here’s the upper part of Kneser‘s neighbourhood graph of the Niemeier lattices:

The Leech lattice has a unique neighbour, that is, among the $23$ remaining Niemeier lattices there is a unique one, $(A_1^{24})^+$, sharing an index two sub-lattice with the Leech.

How would you try to construct $(A_1^{24})^+$, an even unimodular lattice having the same roots as $A_1^{24}$?

The root lattice $A_1$ is $\sqrt{2} \mathbb{Z}$. It has two roots $\pm \sqrt{2}$, determinant $2$, its dual lattice is $A_1^* = \tfrac{1}{\sqrt{2}} \mathbb{Z}$ and we have $A_1^*/A_1 \simeq C_2 \simeq \mathbb{F}_2$.

Thus, $A_1^{24}= \sqrt{2} \mathbb{Z}^{\oplus 24}$ has $48$ roots, determinant $2^{24}$, its dual lattice is $(A_1^{24})^* = \tfrac{1}{\sqrt{2}} \mathbb{Z}^{\oplus 24}$ and the quotient group $(A_1^{24})^*/A_1^{24}$ is $C_2^{24}$ isomorphic to the additive subgroup of $\mathbb{F}_2^{\oplus 24}$.

A larger lattice $A_1^{24} \subseteq L$ of index $k$ gives for the dual lattices an extension $L^* \subseteq (A_1^{24})^*$, also of index $k$. If $L$ were unimodular, then the index has to be $2^{12}$ because we have the situation
\[
A_1^{24} \subseteq L = L^* \subseteq (A_1^{24})^* \]
So, Kneser’s glue vectors form a $12$-dimensional subspace $\mathcal{C}$ in $\mathbb{F}_2^{\oplus 24}$, that is,
\[
L = \mathcal{C} \underset{\mathbb{F}_2}{\times} (A_1^{24})^* = \{ \tfrac{1}{\sqrt{2}} \vec{v} ~|~\vec{v} \in \mathbb{Z}^{\oplus 24},~v=\vec{v}~mod~2 \in \mathcal{C} \} \]
Because $L = L^*$, the linear code $\mathcal{C}$ must be self-dual meaning that $v.w = 0$ (in $\mathbb{F}_2$) for all $v,w \in \mathcal{C}$. Further, we want that the roots of $A_1^{24}$ and $L$ are the same, so the minimal number of non-zero coordinates in $v \in \mathcal{C}$ must be $8$.

That is, $\mathcal{C}$ must be a self-dual binary code of length $24$ with Hamming distance $8$.

Marcel Golay (1902-1989) – Photo Credit

We now know that there is a unique such code, the (extended) binary Golay code, $\mathcal{C}_{24}$, which has

one vector of weight $0$
$759$ vectors of weight $8$ (called ‘octads’)
$2576$ vectors of weight $12$ (called ‘dodecads’)
$759$ vectors of weight $16$
one vector of weight $24$

The $759$ octads form a Steiner system $S(5,8,24)$ (that is, for any $5$-subset $S$ of the $24$-coordinates there is a unique octad having its non-zero coordinates containing $S$).

Witt constructed a Steiner system $S(5,8,24)$ in his 1938 paper “Die $5$-fach transitiven Gruppen von Mathieu”, so it is not unthinkable that he checked the subspace of $\mathbb{F}_2^{\oplus 24}$ spanned by his $759$ octads to be $12$-dimensional and self-dual, thereby constructing the Niemeier-lattice $(A_1^{24})^+$ on that sunday in 1940.

John Conway classified all nine self-dual codes of length $24$ in which the weight
of every codeword is a multiple of $4$. Each one of these codes $\mathcal{C}$ gives a Niemeier lattice $\mathcal{C} \underset{\mathbb{F}_2}{\times} (A_1^{24})^*$, all but one of them having more roots than $A_1^{24}$.

Vera Pless and Neil Sloan classified all $26$ binary self-dual codes of length $24$.