Tag: Kapranov

F_un and braid groups

Published June 15, 2008 by lievenlb

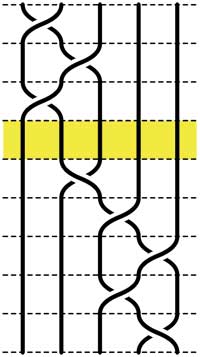
Recall that an n-braid consists of n strictly descending elastic strings connecting n inputs at the top (named 1,2,…,n) to n outputs at the bottom (labeled 1,2,…,n) upto isotopy (meaning that we may pull and rearrange the strings in any way possible within 3-dimensional space). We can always change the braid slightly such that we can divide the interval between in- and output in a number of subintervals such that in each of those there is at most one crossing.

n-braids can be multiplied by putting them on top of each other and connecting the outputs of the first braid trivially to the inputs of the second. For example the 5-braid on the left can be written as $B=B_1.B_2 $ with $B_1 $ the braid on the top 3 subintervals and $B_2 $ the braid on the lower 5 subintervals.

In this way (and using our claim that there can be at most 1 crossing in each subinterval) we can write any n-braid as a word in the generators $\sigma_i $ (with $1 \leq i < n $) being the overcrossing between inputs i and i+1. Observe that the undercrossing is then the inverse $\sigma_i^{-1} $. For example, the braid on the left corresponds to the word

$\sigma_1^{-1}.\sigma_2^{-1}.\sigma_1^{-1}.\sigma_2.\sigma_3^{-1}.\sigma_4^{-1}.\sigma_3^{-1}.\sigma_4 $

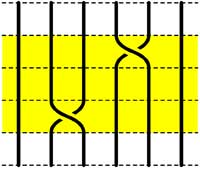
Clearly there are relations among words in the generators. The easiest one we have already used implicitly namely that $\sigma_i.\sigma_i^{-1} $ is the trivial braid. Emil Artin proved in the 1930-ies that all such relations are consequences of two sets of ‘obvious’ relations. The first being commutation relations between crossings when the strings are far enough from each other. That is we have

$\sigma_i . \sigma_j = \sigma_j . \sigma_i $ whenever $|i-j| \geq 2 $

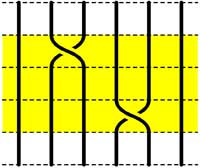The second basic set of relations involves crossings using a common string

$\sigma_i.\sigma_{i+1}.\sigma_i = \sigma_{i+1}.\sigma_i.\sigma_{i+1} $

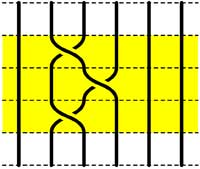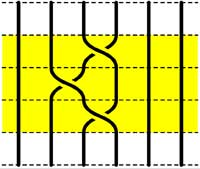
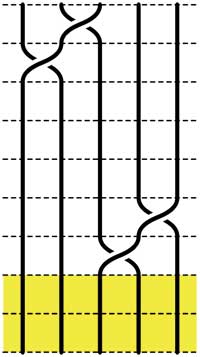
Starting with the 5-braid at the top, we can use these relations to reduce it to a simpler form. At each step we have outlined to region where the relations are applied

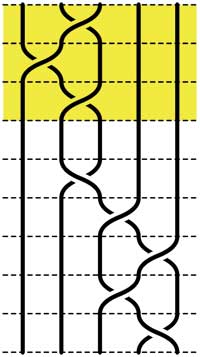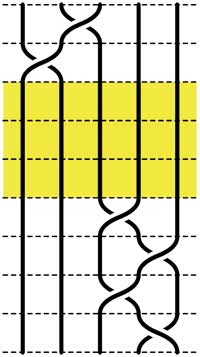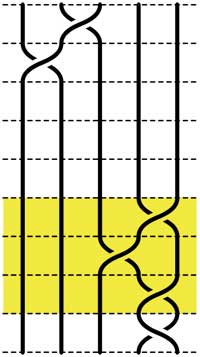These beautiful braid-pictures were produced using the braid-metapost program written by Stijn Symens.

Tracing a string from an input to an output assigns to an n-braid a permutation on n letters. In the above example, the permutation is $~(1,2,4,5,3) $. As this permutation doesn’t change under applying basic reduction, this gives a group-morphism

$\mathbb{B}_n \rightarrow S_n $

from the braid group on n strings $\mathbb{B}_n $ to the symmetric group. We have seen before that the symmetric group $S_n $ has a F-un interpretation as the linear group $GL_n(\mathbb{F}_1) $ over the field with one element. Hence, we can ask whether there is also a F-un interpretation of the n-string braid group and of the above group-morphism.

Kapranov and Smirnov suggest in their paper that the n-string braid group $\mathbb{B}_n \simeq GL_n(\mathbb{F}_1[t]) $ is the general linear group over the polynomial ring $\mathbb{F}_1[t] $ over the field with one element and that the evaluation morphism (setting t=0)

$GL_n(\mathbb{F}_1[t]) \rightarrow GL_n(\mathbb{F}1) $ gives the groupmorphism $\mathbb{B}_n \rightarrow S_n $

The rationale behind this analogy is a theorem of Drinfeld‘s saying that over a finite field $\mathbb{F}_q $, the profinite completion of $GL_n(\mathbb{F}_q[t]) $ is embedded in the fundamental group of the space of q-polynomials of degree n in much the same way as the n-string braid group $\mathbb{B}_n $ is the fundamental group of the space of complex polynomials of degree n without multiple roots.

And, now that we know the basics of absolute linear algebra, we can give an absolute braid-group representation

$\mathbb{B}_n = GL_n(\mathbb{F}_1[t]) \rightarrow GL_n(\mathbb{F}_{1^n}) $

obtained by sending each generator $\sigma_i $ to the matrix over $\mathbb{F}_{1^n} $ (remember that $\mathbb{F}_{1^n} = (\mu_n)^{\bullet} $ where $\mu_n = \langle \epsilon_n \rangle $ are the n-th roots of unity)

$\sigma_i \mapsto \begin{bmatrix}
1_{i-1} & & & \\
& 0 & \epsilon_n & \\
& \epsilon_n^{-1} & 0 & \\
& & & 1_{n-1-i} \end{bmatrix} $

and it is easy to see that these matrices do indeed satisfy Artin’s defining relations for $\mathbb{B}_n $.

5 Comments

Absolute linear algebra

Published June 10, 2008 by lievenlb

Today we will define some basic linear algebra over the absolute fields $\mathbb{F}_{1^n} $ following the Kapranov-Smirnov document. Recall from last time that $\mathbb{F}_{1^n} = \mu_n^{\bullet} $ and that a d-dimensional vectorspace over this field is a pointed set $V^{\bullet} $ where $V $ is a free $\mu_n $-set consisting of n.d elements. Note that in absolute linear algebra we are not allowed to have addition of vectors and have to define everything in terms of scalar multiplication (or if you want, the $\mu_n $-action). In the hope of keeping you awake, we will include an F-un interpretation of the power residue symbol.

Direct sums of vectorspaces are defined via $V^{\bullet} \oplus W^{\bullet} = (V \bigsqcup W)^{\bullet} $, that is, correspond to the disjoint union of free $\mu_n $-sets. Consequently we have that $dim(V^{\bullet} \oplus W^{\bullet}) = dim(V^{\bullet}) + dim(W^{\bullet}) $.

For tensor-product we start with $V^{\bullet} \times W^{\bullet} = (V \times W)^{\bullet} $ the vectorspace cooresponding to the Cartesian product of free $\mu_n $-sets. If the dimensions of $V^{\bullet} $ and $W^{\bullet} $ are respectively d and e, then $V \times W $ consists of n.d.n.e elements, so is of dimension n.d.e. In order to have a sensible notion of tensor-products we have to eliminate the n-factor. We do this by identifying $~(x,y) $ with $(\epsilon_n x, \epsilon^{-1} y) $ and call the corresponding vectorspace $V^{\bullet} \otimes W^{\bullet} $. If we denote the image of $~(x,y) $ by $x \otimes w $ then the identification merely says we can pull the $\mu_n $-action through the tensor-sign, as we’d like to do. With this definition we do indeed have that $dim(V^{\bullet} \otimes W^{\bullet}) = dim(V^{\bullet}) dim(W^{\bullet}) $.

Recall that any linear automorphism $A $ of an $\mathbb{F}_{1^n} $ vectorspace $V^{\bullet} $ with basis ${ b_1,\ldots,b_d } $ (representants of the different $\mu_n $-orbits) is of the form $A(b_i) = \epsilon_n^{k_i} b_{\sigma(i)} $ for some powers of the primitive n-th root of unity $\epsilon_n $ and some permutation $\sigma \in S_d $. We define the determinant $det(A) = \prod_{i=1}^d \epsilon_n^{k_i} $. One verifies that the determinant is multiplicative and independent of the choice of basis.

For example, scalar-multiplication by $\epsilon_n $ gives an automorphism on any $d $-dimensional $\mathbb{F}_{1^n} $-vectorspace $V^{\bullet} $ and the corresponding determinant clearly equals $det = \epsilon_n^d $. That is, the det-functor remembers the dimension modulo n. These mod-n features are a recurrent theme in absolute linear algebra. Another example, which will become relevant when we come to reciprocity laws :

Take $n=2 $. Then, a $\mathbb{F}_{1^2} $ vectorspace $V^{\bullet} $ of dimension d is a set consisting of 2d elements $V $ equipped with a free involution. Any linear automorphism $A~:~V^{\bullet} \rightarrow V^{\bullet} $ is represented by a $d \times d $ matrix having one nonzero entry in every row and column being equal to +1 or -1. Hence, the determinant $det(A) \in \{ +1,-1 \} $.

On the other hand, by definition, the linear automorphism $A $ determines a permutation $\sigma_A \in S_{2d} $ on the 2d non-zero elements of $V^{\bullet} $. The connection between these two interpretations is that $det(A) = sgn(\sigma_A) $ the determinant gives the sign of the permutation!

For a prime power $q=p^k $ with $q \equiv 1~mod(n) $, we have seen that the roots of unity $\mu_n \subset \mathbb{F}_q^* $ and hence that $\mathbb{F}_q $ is a vectorspace over $\mathbb{F}_{1^n} $. For any field-unit $a \in \mathbb{F}_q^* $ we have the power residue symbol

$\begin{pmatrix} a \\ \mathbb{F}_q \end{pmatrix}_n = a^{\frac{q-1}{n}} \in \mu_n $

On the other hand, multiplication by $a $ is a linear automorphism on the $\mathbb{F}_{1^n} $-vectorspace $\mathbb{F}_q $ and hence we can look at its F-un determinant $det(a \times) $. The F-un interpretation of a classical lemma by Gauss asserts that the power residue symbol equals $det(a \times) $.

An $\mathbb{F}_{1^n} $-subspace $W^{\bullet} $ of a vectorspace $V^{\bullet} $ is a subset $W \subset V $ consisting of full $\mu_n $-orbits. Normally, in defining a quotient space we would say that two V-vectors are equivalent when their difference belongs to W and take equivalence classes. However, in absolute linear algebra we are not allowed to take linear combinations of vectors…

The only way out is to define $~(V/W)^{\bullet} $ to correspond to the free $\mu_n $-set $~(V/W) $ obtained by identifying all elements of W with the zero-element in $V^{\bullet} $. But… this will screw-up things if we want to interpret $\mathbb{F}_q $-vectorspaces as $\mathbb{F}_{1^n} $-spaces whenever $q \equiv 1~mod(n) $.

For this reason, Kapranov and Smirnov invent the notion of an equivalence $f~:~X^{\bullet} \rightarrow Y^{\bullet} $ between $\mathbb{F}_{1^n} $-spaces to be a linear map (note that this means a set-theoretic map $X \rightarrow Y^{\bullet} $ such that the invers image of 0 consists of full $\mu_n $-orbits and is a $\mu_n $-map elsewhere) satisfying the properties that $f^{-1}(0) = 0 $ and for every element $y \in Y $ we have that the number of pre-images $f^{-1}(y) $ is congruent to 1 modulo n. Observe that under an equivalence $f~:~X^{\bullet} \rightarrow Y^{\bullet} $ we have that $dim(X^{\bullet}) \equiv dim(Y^{\bullet})~mod(n) $.

This then allows us to define an exact sequence of $\mathbb{F}_{1^n} $-vectorspaces to be

[tex]\xymatrix{0 \ar[r] & V_1^{\bullet} \ar[r]^{\alpha} & V^{\bullet} \ar[r]^{\beta} & V_2^{\bullet} \ar[r] & 0}[/tex]

with $\alpha $ a set-theoretic inclusion, the composition $\beta \circ \alpha $ to be the zero-map and with the additional assumption that the map induced by $\beta $

$~(V/V_1)^{\bullet} \rightarrow V_2^{\bullet} $

is an equivalence. For an exact sequence of spaces as above we have the congruence relation on their dimensions $dim(V_1)+dim(V_2) \equiv dim(V)~mod(n) $.

More importantly, if as before $q \equiv 1~mod(n) $ and we use the embedding $\mu_n \subset \mathbb{F}_q^* $ to turn usual $\mathbb{F}_q $-vectorspaces into absolute $\mathbb{F}_{1^n} $-spaces, then an ordinary exact sequence of $\mathbb{F}_q $-vectorspaces remains exact in the above definition.

2 Comments

The F_un folklore

Published June 7, 2008 by lievenlb

All esoteric subjects have their own secret (sacred) texts. If you opened the Da Vinci Code (or even better, the original The Holy blood and the Holy grail) you will known about a mysterious collection of documents, known as the “Dossiers secrets“, deposited in the Bibliothèque nationale de France on 27 April 1967, which is rumoured to contain the mysteries of the Priory of Sion, a secret society founded in the middle ages and still active today…

The followers of F-un, for $\mathbb{F}_1 $ the field of one element, have their own collection of semi-secret texts, surrounded by whispers, of which they try to decode every single line in search of enlightenment. Fortunately, you do not have to search the shelves of the Bibliotheque National in Paris, but the depths of the internet to find them as huge, bandwidth-unfriendly, scanned documents.

The first are the lecture notes “Lectures on zeta functions and motives” by Yuri I. Manin of a course given in 1991.

One can download a scanned version of the paper from the homepage of Katia Consani as a huge 23.1 Mb file. Of F-un relevance is the first section “Absolute Motives?” in which

“…we describe a highly speculative picture of analogies between arithmetics over $\mathbb{F}_q $ and over $\mathbb{Z} $, cast in the language reminiscent of Grothendieck’s motives. We postulate the existence of a category with tensor product $\times $ whose objects correspond not only to the divisors of the Hasse-Weil zeta functions of schemes over $\mathbb{Z} $, but also to Kurokawa’s tensor divisors. This neatly leads to teh introduction of an “absolute Tate motive” $\mathbb{T} $, whose zeta function is $\frac{s-1}{2\pi} $, and whose zeroth power is “the absolute point” which is teh base for Kurokawa’s direct products. We add some speculations about the role of $\mathbb{T} $ in the “algebraic geometry over a one-element field”, and in clarifying the structure of the gamma factors at infinity.” (loc.cit. p 1-2)

I’d welcome links to material explaining this section to people knowing no motives.

The second one is the unpublished paper “Cohomology determinants and reciprocity laws : number field case” by Mikhail Kapranov and A. Smirnov.

This paper features in blog-posts at the Arcadian Functor, in John Baez’ Weekly Finds and in yesterday’s post at Noncommutative Geometry.

You can download every single page (of 15) as a separate file from here. But, in order to help spreading the Fun-gospel, I’ve made these scans into a single PDF-file which you can download as a 2.6 Mb PDF. In the introduction they say :

“First of all, it is an old idea to interpret combinatorics of finite sets as the $q \rightarrow 1 $ limit of linear algebra over the finite field $\mathbb{F}_q $. This had lead to frequent consideration of the folklore object $\mathbb{F}_1 $, the “field with one element”, whose vector spaces are just sets. One can postulate, of course, that $\mathbf{spec}(\mathbb{F}_1) $ is the absolute point, but the real problem is to develop non-trivial consequences of this point of view.”

They manage to deduce higher reciprocity laws in class field theory within the theory of $\mathbb{F}_1 $ and its field extensions $\mathbb{F}_{1^n} $. But first, let us explain how they define linear algebra over these absolute fields.

Here is a first principle : in doing linear algebra over these fields, there is no additive structure but only scalar multiplication by field elements. So, what are vector spaces over the field with one element? Well, as scalar multiplication with 1 is just the identity map, we have that a vector space is just a set. Linear maps are just set-maps and in particular, a linear isomorphism of a vector space onto itself is a permutation of the set. That is, linear algebra over $\mathbb{F}_1 $ is the same as combinatorics of (finite) sets.

A vector space over $\mathbb{F}_1 $ is just a set; the dimension of such a vector space is the cardinality of the set. The general linear group $GL_n(\mathbb{F}_1) $ is the symmetric group $S_n $, the identification via permutation matrices (having exactly one 1 in every row and column)

Some people prefer to view an $\mathbb{F}_1 $ vector space as a pointed set, the special element being the ‘origin’ $0 $ but as $\mathbb{F}_1 $ doesnt have a zero, there is also no zero-vector. Still, in later applications (such as defining exact sequences and quotient spaces) it is helpful to have an origin. So, let us denote for any set $S $ by $S^{\bullet} = S \cup { 0 } $. Clearly, linear maps between such ‘extended’ spaces must be maps of pointed sets, that is, sending $0 \rightarrow 0 $.

The field with one element $\mathbb{F}_1 $ has a field extension of degree n for any natural number n which we denote by $\mathbb{F}_{1^n} $ and using the above notation we will define this field as :

$\mathbb{F}_{1^n} = \mu_n^{\bullet} $ with $\mu_n $ the group of all n-th roots of unity. Note that if we choose a primitive n-th root $\epsilon_n $, then $\mu_n \simeq C_n $ is the cyclic group of order n.

Now what is a vector space over $\mathbb{F}_{1^n} $? Recall that we only demand units of the field to act by scalar multiplication, so each ‘vector’ $\vec{v} $ determines an n-set of linear dependent vectors $\epsilon_n^i \vec{v} $. In other words, any $\mathbb{F}_{1^n} $-vector space is of the form $V^{\bullet} $ with $V $ a set of which the group $\mu_n $ acts freely. Hence, $V $ has $N=d.n $ elements and there are exactly $d $ orbits for the action of $\mu_n $ by scalar multiplication. We call $d $ the dimension of the vectorspace and a basis consists in choosing one representant for every orbits. That is, $~B = { b_1,\ldots,b_d } $ is a basis if (and only if) $V = { \epsilon_n^j b_i~:~1 \leq i \leq d, 1 \leq j \leq n } $.

So, vectorspaces are free $\mu_n $-sets and hence linear maps $V^{\bullet} \rightarrow W^{\bullet} $ is a $\mu_n $-map $V \rightarrow W $. In particular, a linear isomorphism of $V $, that is an element of $GL_d(\mathbb{F}_{1^n}) $ is a $\mu_n $ bijection sending any basis element $b_i \rightarrow \epsilon_n^{j(i)} b_{\sigma(i)} $ for a permutation $\sigma \in S_d $.

An $\mathbb{F}_{1^n} $-vectorspace $V^{\bullet} $ is a free $\mu_n $-set $V $ of $N=n.d $ elements. The dimension $dim_{\mathbb{F}_{1^n}}(V^{\bullet}) = d $ and the general linear group $GL_d(\mathbb{F}_{1^n}) $ is the wreath product of $S_d $ with $\mu_n^{\times d} $, the identification as matrices with exactly one non-zero entry (being an n-th root of unity) in every row and every column.

This may appear as a rather sterile theory, so let us give an extremely important example, which will lead us to our second principle for developing absolute linear algebra.

Let $q=p^k $ be a prime power and let $\mathbb{F}_q $ be the finite field with $q $ elements. Assume that $q \cong 1~mod(n) $. It is well known that the group of units $\mathbb{F}_q^{\ast} $ is cyclic of order $q-1 $ so by the assumption we can identify $\mu_n $ with a subgroup of $\mathbb{F}_q^{\ast} $.

Then, $\mathbb{F}_q = (\mathbb{F}_q^{\ast})^{\bullet} $ is an $\mathbb{F}_{1^n} $-vectorspace of dimension $d=\frac{q-1}{n} $. In other words, $\mathbb{F}_q $ is an $\mathbb{F}_{1^n} $-algebra. But then, any ordinary $\mathbb{F}_q $-vectorspace of dimension $e $ becomes (via restriction of scalars) an $\mathbb{F}_{1^n} $-vector space of dimension $\frac{e(q-1)}{n} $.

Next time we will introduce more linear algebra definitions (including determinants, exact sequences, direct sums and tensor products) in the realm the absolute fields $\mathbb{F}_{1^n} $ and remarkt that we have to alter the known definitions as we can only use the scalar-multiplication. To guide us, we have the second principle : all traditional results of linear algebra over $\mathbb{F}_q $ must be recovered from the new definitions under the vector-space identification $\mathbb{F}_q = (\mathbb{F}_q^{\ast})^{\bullet} = \mathbb{F}_{1^n} $ when $n=q-1 $. (to be continued)

One Comment