The Leech lattice was, according to wikipedia, ‘originally discovered by Ernst Witt in 1940, but he did not publish his discovery’ and it ‘was later re-discovered in 1965 by John Leech’. However, there is very little evidence to support this claim.
The facts
What is certain is that John Leech discovered in 1965 an amazingly dense 24-dimensional lattice $ {\Lambda} $ having the property that unit balls around the lattice points touch, each one of them having exactly 196560 neighbors. The paper ‘Notes on sphere packings’ appeared in 1967 in the Canad. J. Math. 19, 251-267.
Compare this to the optimal method to place pennies on a table, leading to the hexagonal tiling, each penny touching exactly 6 others. Similarly, in dimension 8 the densest packing is the E8 lattice in which every unit ball has exactly 240 neighbors.
The Leech lattice $ {\Lambda} $ can be characterized as the unique unimodular positive definite even lattice such that the length of any non-zero vector is at least two.
The list of all positive definite even unimodular lattices, $ {\Gamma_{24}} $, in dimension 24 was classified later by Hans-Volker Niemeier and are now known as the 24 Niemeier lattices.
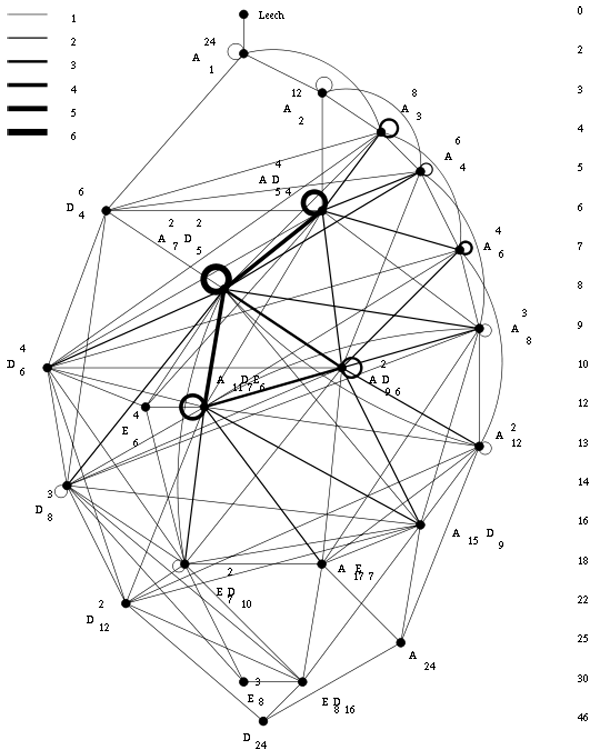
For the chronology below it is perhaps useful to note that, whereas Niemeier’s paper did appear in 1973, it was submitted april 5th 1971 and is just a minor rewrite of Niemeier’s Ph.D. “Definite quadratische Formen der Dimension 24 und Diskriminante 1” obtained in 1968 from the University of Göttingen with advisor Martin Kneser.
The claim
On page 328 of Ernst Witt’s Collected Papers Ina Kersten recalls that Witt gave a colloquium talk on January 27, 1970 in Hamburg entitled “Gitter und Mathieu-Gruppen” (Lattices and Mathieu-groups). In this talk Witt claimed to have found nine lattices in $ {\Gamma_{24}} $ as far back as 1938 and that on January 28, 1940 he found two additional lattices $ {M} $ and $ {\Lambda} $ while studying the Steiner system $ {S(5,8,24)} $.
On page 329 of the collected papers is a scan of the abstract Witt wrote in the colloquium book in Bielefeld where he gave a talk “Uber einige unimodularen Gitter” (On certain unimodular lattices) on January 28, 1972

Here, Witt claims that he found three new lattices in $ {\Gamma_{24}} $ on January 28, 1940 as the lattices $ {M} $, $ {M’} $ and $ {\Lambda} $ ‘feiern heute ihren 32sten Gebursttag!’ (celebrate today their 32nd birthday).
He goes on telling that the lattices $ {M} $ and $ {\Lambda} $ were number 10 and 11 in his list of lattices in $ {\Gamma_{24}} $ in his paper “Eine Identität zwischen Modulformen zweiten Grades” in the Abh. Math. Sem. Univ. Hamburg 14 (1941) 323-337 and he refers in particular to page 324 of that paper.
He further claims that he computed the orders of their automorphism groups and writes that $ {\Lambda} $ ‘wurde 1967 von Leech wieder-entdeckt’ (was re-discovered by Leech in 1967) and that its automorphism group $ {G(\Lambda)} $ was studied by John Conway. Recall that Conway’s investigations of the automorphism group of the Leech lattice led to the discovery of three new sporadic groups, the Conway groups $ {Co_1,Co_2} $ and $ {Co_3} $.
However, Witt’s 1941-paper does not contain a numbered list of 24-dimensional lattices. In fact, apart from $ {E_8+E_8+E_8} $ is does not contain a single lattice in $ {\Gamma_{24}} $. The only relevant paragraph is indeed on page 324

He observes that Mordell already proved that there is just one lattice in $ {\Gamma_8} $ (the $ {E_8} $-lattice) and that the main result of his paper is to prove that there are precisely two even unimodular 16-dimensional lattices : $ {E_8+E_8} $ and another lattice, now usually called the 16-dimensional Witt-lattice.
He then goes on to observe that Schoeneberg knew that $ {\# \Gamma_{24} > 1} $ and so there must be more lattices than $ {E_8+E_8+E_8} $ in $ {\Gamma_{24}} $. Witt concludes with : “In my attempt to find such a lattice, I discovered more than 10 lattices in $ {\Gamma_{24}} $. The determination of $ {\# \Gamma_{24}} $ does not seem to be entirely trivial.”
Hence, it is fair to assume that by 1940 Ernst Witt had discovered at least 11 of the 24 Niemeier lattices. Whether the Leech lattice was indeed lattice 11 on the list is anybody’s guess.
Next time we will look more closely into the historical context of Witt’s 1941 paper.
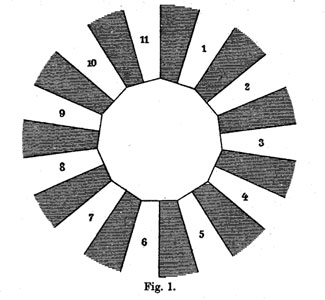
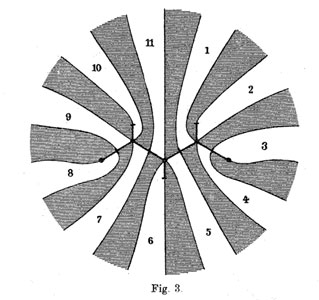
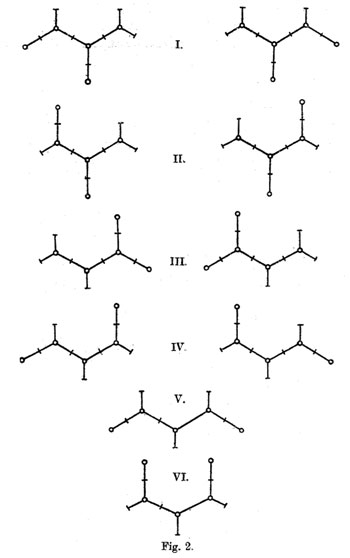 The ramification data translates to the following statements about the Linienzuge : (a) it must be a tree ($\infty $ has one preimage), (b) there are exactly 11 (half)edges (the degree of the cover),
The ramification data translates to the following statements about the Linienzuge : (a) it must be a tree ($\infty $ has one preimage), (b) there are exactly 11 (half)edges (the degree of the cover),
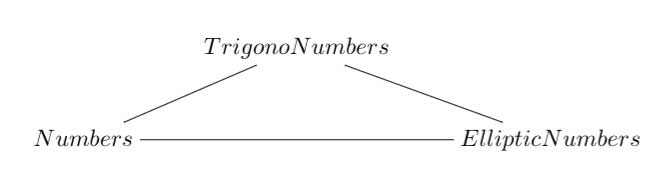
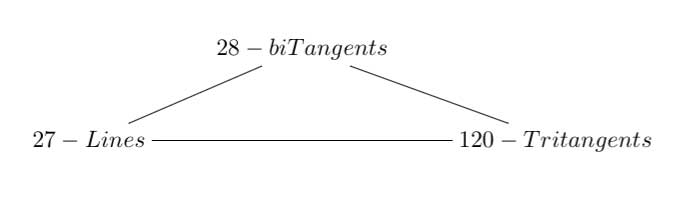
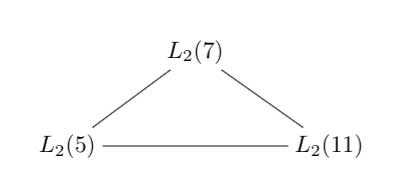
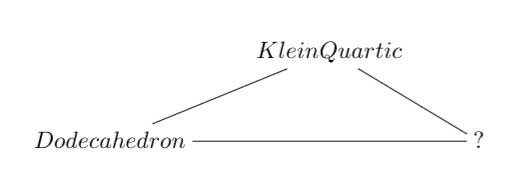
 Referring to the triple of exceptional Galois groups $L_2(5),L_2(7),L_2(11) $ and its connection to the Platonic solids I
Referring to the triple of exceptional Galois groups $L_2(5),L_2(7),L_2(11) $ and its connection to the Platonic solids I