Skip to content →

Tag: google

the Reddit (after)effect

Published January 15, 2011 by lievenlb

Sunday january 2nd around 18hr NeB-stats went crazy.

Referrals clarified that the post ‘What is the knot associated to a prime?’ was picked up at Reddit/math and remained nr.1 for about a day.

Now, the dust has settled, so let’s learn from the experience.

A Reddit-mention is to a blog what doping is to a sporter.

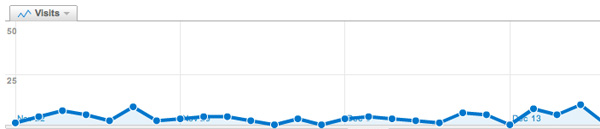
You get an immediate boost in the most competitive of all blog-stats, the number of unique vistors (blue graph), but is doesn’t result in a long-term effect, and, it may even be harmful to more essential blog-stats, such as the average time visitors spend on your site (yellow graph).

For NeB the unique vistors/day fluctuate normally around 300, but peaked to 1295 and 1733 on the ‘Reddit-days’. In contrast, the avg. time on site is normally around 3 minutes, but dropped the same days to 44 and 30 seconds!

Whereas some of the Reddits spend enough time to read the post and comment on it, the vast majority zap from one link to the next. Having monitored the Reddit/math page for two weeks, I’m convinced that post only made it because it was visually pretty good. The average Reddit/math-er is a viewer more than a reader…

So, should I go for shorter, snappier, more visual posts?

Let’s compare Reddits to those coming from the three sites giving NeB most referrals : Google search, MathOverflow and Wikipedia.

This is the traffic coming from Reddit/math, as always the blue graph are the unique visitors, the yellow graph their average time on site, blue-scales to the left, yellow-scales to the right.

Here’s the same graph for Google search. The unique visitors/day fluctuate around 50 and their average time on site about 2 minutes.

The math-related search terms most used were this month : ‘functor of point approach’, ‘profinite integers’ and ‘bost-connes sytem’.

More rewarding to me are referrals from MathOverflow.

The number of visitors depends on whether the MathO-questions made it to the front-page (for example, the 80 visits on december 15, came from the What are dessins d’enfants?-topic getting an extra comment that very day, and having two references to NeB-posts : The best rejected proposal ever and Klein’s dessins d’enfant and the buckyball), but even older MathO-topics give a few referrals a day, and these people sure take their time reading the posts (+ 5 minutes).

Other MathO-topics giving referrals this month were Most intricate and most beautiful structures in mathematics (linking to Looking for F-un), What should be learned in a first serious schemes course? (linking to Mumford’s treasure map (btw. one of the most visited NeB-posts ever)), How much of scheme theory can you visualize? (linking again to Mumford’s treasure map) and Approaches to Riemann hypothesis using methods outside number theory (linking to the Bost-Connes series).

Finally, there’s Wikipedia

giving 5 to 10 referrals a day, with a pretty good time-on-site average (around 4 minutes, peaking to 12 minutes). It is rewarding to see NeB-posts referred to in as diverse Wikipedia-topics as ‘Fifteen puzzle’, ‘Field with one element’, ‘Evariste Galois’, ‘ADE classification’, ‘Monster group’, ‘Arithmetic topology’, ‘Dessin d’enfant’, ‘Groupoid’, ‘Belyi’s theorem’, ‘Modular group’, ‘Cubic surface’, ‘Esquisse d’un programme’, ‘N-puzzle’, ‘Shabat polynomial’ and ‘Mathieu group’.

What lesson should be learned from all this data? Should I go for shorter, snappier and more visual posts, or should I focus on the small group of visitors taking their time reading through a longer post, and don’t care about the appallingly high bounce rate the others cause?

8 Comments

NeB : 7 years and now an iPad App

Published December 31, 2010 by lievenlb

Exactly 7 years ago I wrote my first post. This blog wasn’t called NeB yet and it used pMachine, a then free blogging tool (later transformed into expression engine), rather than WordPress.

Over the years NeB survived three hardware-upgrades of ‘the Matrix’ (the webserver hosting it), more themes than I care to remember, and a couple of dramatic closure announcements…

But then we’re still here, soldiering on, still uncertain whether there’s a point to it, but grateful for tiny tokens of appreciation.

Such as this morning’s story: Chandan deemed it necessary to correct two spelling mistakes in a 2 year old Fun-math post on Weil and the Riemann hypothesis (also reposted on Neb here). Often there’s a story behind such sudden comments, and a quick check of MathOverflow revealed this answer and the comments following it.

I thank Ed Dean for linking to the Fun-post, Chandan for correcting the misspellings and Georges for the kind words. I agree with Georges that a cut&copy of a blogpost-quoted text does not require a link to that post (though it is always much appreciated). It is rewarding to see such old posts getting a second chance…

Above the Google Analytics graph of the visitors coming here via a mobile device (at most 5 on a good day…). Anticipating much more iPads around after tonights presents-session I’ve made NeB more accessible for iPods, iPhones, iPads and other mobile devices.

The first time you get here via your Mac-device of choice you’ll be given the option of saving NeB as an App. It has its own icon (lowest row middle, also the favicon of NeB) and flashy start-up screen.

Of course, the whole point trying to make NeB more readable for Mobile users you get an overview of the latest posts together with links to categories and tags and the number of comments. Sliding through you can read the post, optimized for the device.

I do hope you will use the two buttons at the end of each post, the first to share or save it and the second to leave a comment.

I wish you all a lot of mathematical (and other) fun in 2011 :: lieven.

3 Comments

Books Ngram for your upcoming parties

Published December 19, 2010 by lievenlb

No christmas- or new-years family party without heated discussions. Often on quite silly topics.

For example, which late 19th-century bookcharacter turned out to be most influential in the 20th century? Dracula, from the 1897 novel by Irish author Bram Stoker or Sir Arthur Conan Doyle’s Sherlock Holmes who made his first appearance in 1887?

Well, this year you can spice up such futile discussions by going over to Google Labs Books Ngram Viewer, specify the time period of interest to you and the relevant search terms and in no time it spits back a graph comparing the number of books mentioning these terms.

Here’s the 20th-century graph for ‘Dracula’ (blue), compared to ‘Sherlock Holmes’ (red).

The verdict being that Sherlock was the more popular of the two for the better part of the century, but in the end the vampire bit the detective. Such graphs lead to lots of new questions, such as : why was Holmes so popular in the early 30ties? and in WW2? why did Dracula become popular in the late 90ties? etc. etc.

Clearly, once you’ve used Books Ngram it’s a dangerous time-waster. Below, the graphs in the time-frame 1980-2008 for Alain Connes (blue), noncommutative geometry (red), Hopf algebras (green) and quantum groups (yellow).

It illustrates the simultaneous rise and fall of both quantum groups and Hopf algebras, whereas the noncommutative geometry-graph follows that of Alain Connes with a delay of about 2 years. I’m sure you’ll find a good use for this splendid tool…

2 Comments