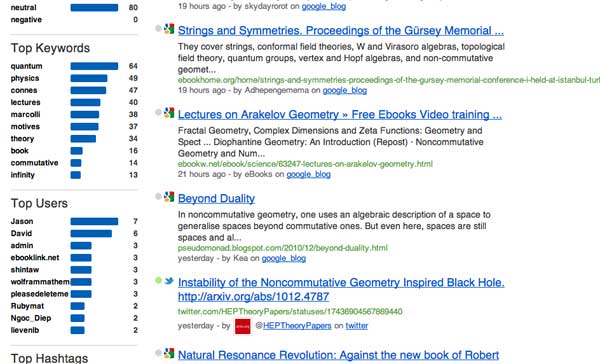
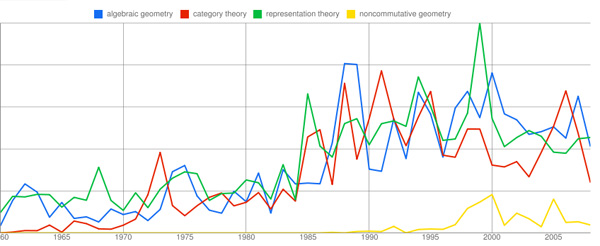
A few MathOverflow threads I bookmarked in 2010 for various reasons.
- Honest answer : Applications of algebraic geometry over a field with one element. James Borger’s answer : “I’m confident that the answer to the original question is no. There are hardly any theorems at all in the subject, much less ones with external applications! In other words, if no further progress is ever made in any of the directions people have pursued, everything will likely be forgotten”
- Unknown result (at least to me) : Irreducibility of polynomials in two variables. Graham Leuschke’s “all-time leading candidate for Most Preposterous Theorem Ever”, proved using the classification of the finite simple groups.
- Should know example (but don’t) : Algebra A with Spec(A) reduced and Rep_n(A) non-reduced. Algebras being commutative here and even the existence of an example with Spec(A) is smooth is open. Peter Samuelson : ” My guess would be yes for both, but I’m not sure how to find one for either one.”
- Great list : The Frobenius morphism. David Ben-Zvi’s “outdated collection of intuitive ways to think about raising to the p-th power”.
- Overrated answer : who fixed the topology on ideles?. John Tate’s answer “When I wrote my thesis I used what seemed to me to be the obvious topology without going into the history of the matter.” got 73 votes…
- Langlands for dummies : What is the L-function version of quadratic reciprocity?. Sometimes working through the easiest non-trivial example gives more insight than several survey papers.