Skip to content →

Tag: games

exotic chess positions (1)

Published March 4, 2008 by lievenlb

Ever tried a chess problem like : White to move, mate in two! Of course you have, and these are pretty easy to solve : you only have to work through the finite list of white first moves and decide whether or not black has a move left preventing mate on the next white move. This is even a (non-optimal) fool-proof algorithm to find the solution to this kind of chess problems. Right?

Wrong! There exist concrete positions, provable mate in two in which it is NOT possible to determine the winning first move for white! So, what’s wrong with the argument above? We did assume that, given the position, it is possible to determine all legal moves for the two players. So?

Well, some moves are legal only depending on the history of the game. For example, you are only allowed to do a castling if your king nor your rook made a prior move. Further, you can only make an en-passant-capture on the next move.

But surely all this is just theoretical? No-one ever constructed a provable 2-mate with impossible winning move. Wrong again. The logician Raymond Smullyan did precisely that in his retro-chess puzzle book Chess mysteries of Sherlock Holmes. Here’s the position :



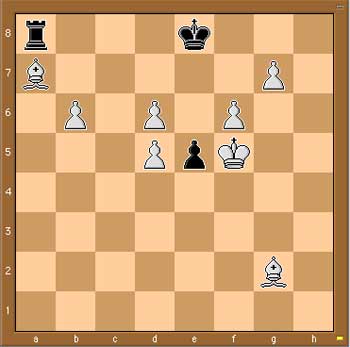
Presumably every chess player goes for the mate : 1. Kf5-e6 2. g7-g8D But what if black counters your first move with a castling 1. … 0-0-0 ? Surely he isnt allowed to do this. Why not, is there any clue in the position to prove that either the king or the rook must have moved before?

Well, what was black previous move then? It cannot be the pawn move e6-e5 as before that move the white King would be in check, so what was it? Just one possibility left : it must have been e7-e5.

This offers then another winning strategy for white, as white can capture en-passant. 1. d5xe6 e.p. and then if black castles 1. … 0.0.0, 2. b6-b7 or is black does any other move : 2. g7-g8.

Hence, whatever the games’ history, white has a mate in two! However, looking ONLY at the given position, it is impossible for him to judge whether Kf5-e6 will do the trick!

Anyone seen similar constructions?

UPDATE

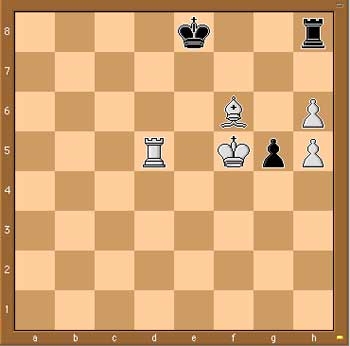
According to the wikipedia page on Retrograde chess analysis, the Smullyan-idea is an adaptation of a much older problem due to W. Langstaff in the Chess Amateur of 1922. Here’s the situation (the solution is the same as above)



4 Comments

Writing & Blogging

Published February 27, 2008 by lievenlb

Terry Tao is reworking some of his better blogposts into a book, to be published by the AMS (here’s a preliminary version of the book “What’s New?”)

After some thought, I decided not to transcribe all of my posts from last year (there are 93 of them!), but instead to restrict attention to those articles which (a) have significant mathematical content, (b) are not announcements of material that will be published elsewhere, and (c) are not primarily based on a talk given by someone else. As it turns out, this still leaves about 33 articles from 2007, leading to a decent-sized book of a couple hundred pages in length.

If you have a blog and want to turn it into a LaTeX-book, there’s no need to transcribe or copy every single post, thanks to the WPTeX tool. Note that this is NOT a WP-plugin, but a (simple at that) php-program which turns all posts into a bookcontent.tex file. This file can then be edited further into a proper book.

Unfortunately, the present version chokes on LaTeXrender-code (which is easy enough to solve doing a global ‘find-and-replace’ of the tex-tags by dollar-signs) but worse, on Markdown-code… But then, someone fluent in php-regex will have no problems extending the libs/functions.php file (I hope…).

At the moment I’m considering turning the Mathieu-games-posts into a booklet. A possible title might be Mathieumatical Games. Rereading them (and other posts) I regret to be such an impatient blogger. Often I’m interested in something and start writing posts about it without knowing where or when I’ll land. This makes my posts a lot harder to get through than they might have been, if I would blog only after having digested the material myself… Typical recent examples are the tori-crypto-posts and the Bost-Connes algebra posts.

So, I still have a lot to learn from other bloggers I admire, such as Jennifer Ouellette who maintains the Coctail Party Physics blog. At the moment, Jennifer is resident blogger-journalist at the Kavli Institute where she is running a “Journal Club” workshop giving ideas on how to write better about science.

But the KITP is also committed to fostering scientific communication. That’s where I come in. Each Friday through April 26th, I’ll be presiding over a “Journal Club” meeting focusing on some aspect of communicating science.

Her most recent talk was entitled To Blog or Not to Blog? That is the Question and you can find the slides as well as a QuickTime movie of her talk. They even plan to set up a blog for the participants of the workshop. I will surely follow the rest of her course with keen interest!

3 Comments

Archimedes’ stomachion

Published February 11, 2008 by lievenlb

The Archimedes codex is a good read, especially when you are (like me) a failed archeologist. The palimpsest (Greek for ‘scraped again’) is the worlds first Kyoto-approved ‘sustainable writing’. Isn’t it great to realize that one of the few surviving texts by Archimedes only made it because some monks recycled an old medieval parchment by scraping off most of the text, cutting the pages in half, rebinding them and writing a song-book on them…

The Archimedes-text is barely visible as vertical lines running through the song-lyrics. There is a great website telling the story in all its detail.

Contrary to what the books claims I don’t think we will have to rewrite maths history. Didn’t we already know that the Greek were able to compute areas and volumes by approximating them with polygons resp. polytopes? Of course one might view this as a precursor to integral calculus… And then the claim that Archimedes invented ordinal calculus. Sure the Greek knew that there were ‘as many’ even integers than integers… No, for me the major surprise was their theory about the genesis of mathematical notation.

The Greek were pure ASCII mathematicians : they wrote their proofs out in full text. Now, here’s an interesting theory how symbols got into maths… pure laziness of the medieval monks transcribing the old works! Copying a text was a dull undertaking so instead of repeating ‘has the same ratio as’ for the 1001th time, these monks introduced abbreviations like $\Sigma $ instead… and from then on things got slightly out of hand.

Another great chapter is on the stomachion, perhaps the oldest mathematical puzzle. Just a few pages made in into the palimpsest so we do not really know what (if anything) Archimedes had to say about it, but the conjecture is that he was after the number of different ways one could make a square with the following 14 pieces

People used computers to show that the total number is $17152=2^8 \times 67 $. The 2-power is hardly surprising in view of symmetries of the square (giving $8 $) and the fact that one can flip one of the two vertical or diagonal parts in the alternative description of the square

but I sure would like to know where the factor 67 is coming from… The MAA and UCSD have some good pages related to the stomachion puzzle. Finally, the book also views the problema bovinum as an authentic Archimedes, so maybe I should stick to my promise to blog about it, after all…

One Comment