Tag: differential

Arnold’s trinities

Published June 17, 2008 by lievenlb

Referring to the triple of exceptional Galois groups $L_2(5),L_2(7),L_2(11) $ and its connection to the Platonic solids I wrote : “It sure seems that surprises often come in triples…”. Briefly I considered replacing triples by trinities, but then, I didnt want to sound too mystic…

David Corfield of the n-category cafe and a dialogue on infinity (and perhaps other blogs I’m unaware of) pointed me to the paper Symplectization, complexification and mathematical trinities by Vladimir I. Arnold. (Update : here is a PDF-conversion of the paper)

The paper is a write-up of the second in a series of three lectures Arnold gave in june 1997 at the meeting in the Fields Institute dedicated to his 60th birthday. The goal of that lecture was to explain some mathematical dreams he had.

The next dream I want to present is an even more fantastic set of theorems and conjectures. Here I also have no theory and actually the ideas form a kind of religion rather than mathematics.
The key observation is that in mathematics one encounters many trinities. I shall present a list of examples. The main dream (or conjecture) is that all these trinities are united by some rectangular “commutative diagrams”.
I mean the existence of some “functorial” constructions connecting different trinities. The knowledge of the existence of these diagrams provides some new conjectures which might turn to be true theorems.

Follows a list of 12 trinities, many taken from Arnold’s field of expertise being differential geometry. I’ll restrict to the more algebraically inclined ones.

1 : “The first trinity everyone knows is”

where $\mathbb{H} $ are the Hamiltonian quaternions. The trinity on the left may be natural to differential geometers who see real and complex and hyper-Kaehler manifolds as distinct but related beasts, but I’m willing to bet that most algebraists would settle for the trinity on the right where $\mathbb{O} $ are the octonions.

2 : The next trinity is that of the exceptional Lie algebras E6, E7 and E8.

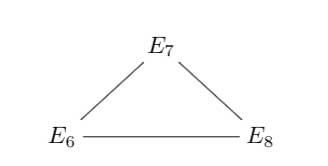
with corresponding Dynkin-Coxeter diagrams

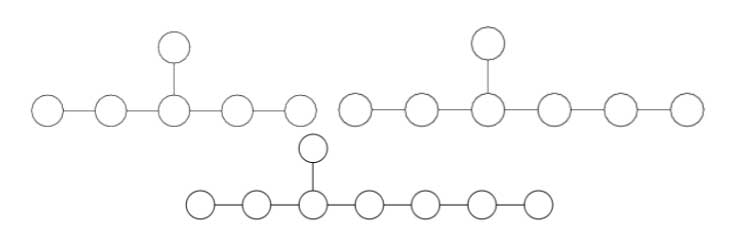
Arnold has this to say about the apparent ubiquity of Dynkin diagrams in mathematics.

Manin told me once that the reason why we always encounter this list in many different mathematical classifications is its presence in the hardware of our brain (which is thus unable to discover a more complicated scheme).
I still hope there exists a better reason that once should be discovered.

Amen to that. I’m quite hopeful human evolution will overcome the limitations of Manin’s brain…

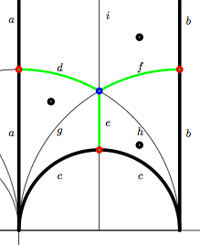
3 : Next comes the Platonic trinity of the tetrahedron, cube and dodecahedron

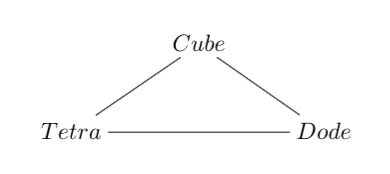
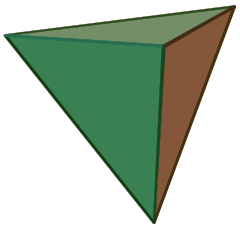
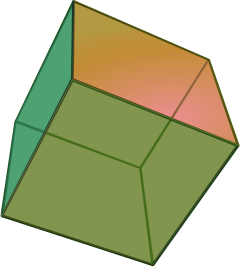
Clearly one can argue against this trinity as follows : a tetrahedron is a bunch of triangles such that there are exactly 3 of them meeting in each vertex, a cube is a bunch of squares, again 3 meeting in every vertex, a dodecahedron is a bunch of pentagons 3 meeting in every vertex… and we can continue the pattern. What should be a bunch a hexagons such that in each vertex exactly 3 of them meet? Well, only one possibility : it must be the hexagonal tiling (on the left below). And in normal Euclidian space we cannot have a bunch of septagons such that three of them meet in every vertex, but in hyperbolic geometry this is still possible and leads to the Klein quartic (on the right). Check out this wonderful post by John Baez for more on this.

4 : The trinity of the rotation symmetry groups of the three Platonics

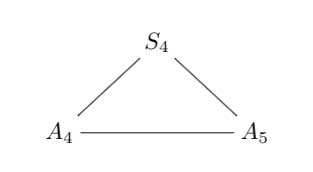
where $A_n $ is the alternating group on n letters and $S_n $ is the symmetric group.

Clearly, any rotation of a Platonic solid takes vertices to vertices, edges to edges and faces to faces. For the tetrahedron we can easily see the 4 of the group $A_4 $, say the 4 vertices. But what is the 4 of $S_4 $ in the case of a cube? Well, a cube has 4 body-diagonals and they are permuted under the rotational symmetries. The most difficult case is to see the $5 $ of $A_5 $ in the dodecahedron. Well, here’s the solution to this riddle

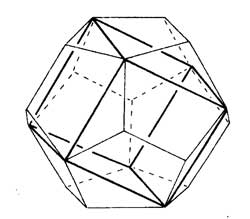
there are exactly 5 inscribed cubes in a dodecahedron and they are permuted by the rotations in the same way as $A_5 $.

7 : The seventh trinity involves complex polynomials in one variable

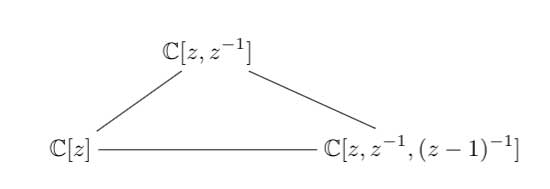
the Laurant polynomials and the modular polynomials (that is, rational functions with three poles at 0,1 and $\infty $.

8 : The eight one is another beauty

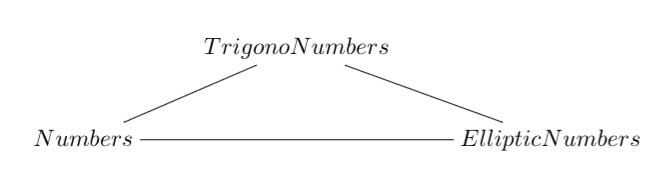
Here ‘numbers’ are the ordinary complex numbers $\mathbb{C} $, the ‘trigonometric numbers’ are the quantum version of those (aka q-numbers) which is a one-parameter deformation and finally, the ‘elliptic numbers’ are a two-dimensional deformation. If you ever encountered a Sklyanin algebra this will sound familiar.

This trinity is based on a paper of Turaev and Frenkel and I must come back to it some time…

The paper has some other nice trinities (such as those among Whitney, Chern and Pontryagin classes) but as I cannot add anything sensible to it, let us include a few more algebraic trinities. The first one attributed by Arnold to John McKay

13 : A trinity parallel to the exceptional Lie algebra one is

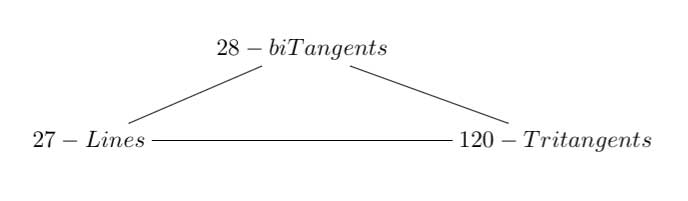
between the 27 straight lines on a cubic surface, the 28 bitangents on a quartic plane curve and the 120 tritangent planes of a canonic sextic curve of genus 4.

14 : The exceptional Galois groups

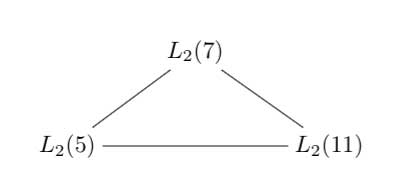
explained last time.

15 : The associated curves with these groups as symmetry groups (as in the previous post)

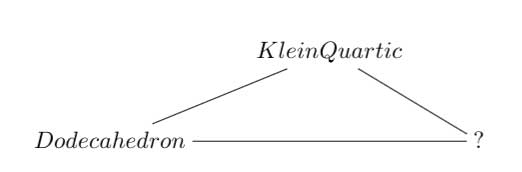
where the ? refers to the mysterious genus 70 curve. I’ll check with one of the authors whether there is still an embargo on the content of this paper and if not come back to it in full detail.

16 : The three generations of sporadic groups

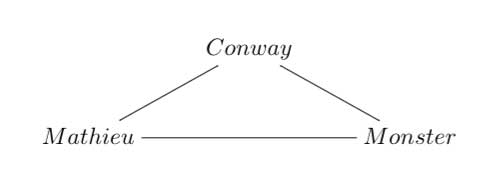
Do you have other trinities you’d like to worship?

Quiver-superpotentials

Published January 14, 2008 by lievenlb

It’s been a while, so let’s include a recap : a (transitive) permutation representation of the modular group $\Gamma = PSL_2(\mathbb{Z}) $ is determined by the conjugacy class of a cofinite subgroup $\Lambda \subset \Gamma $, or equivalently, to a dessin d’enfant. We have introduced a quiver (aka an oriented graph) which comes from a triangulation of the compactification of $\mathbb{H} / \Lambda $ where $\mathbb{H} $ is the hyperbolic upper half-plane. This quiver is independent of the chosen embedding of the dessin in the Dedeking tessellation. (For more on these terms and constructions, please consult the series Modular subgroups and Dessins d’enfants).

Why are quivers useful? To start, any quiver $Q $ defines a noncommutative algebra, the path algebra $\mathbb{C} Q $, which has as a $\mathbb{C} $-basis all oriented paths in the quiver and multiplication is induced by concatenation of paths (when possible, or zero otherwise). Usually, it is quite hard to make actual computations in noncommutative algebras, but in the case of path algebras you can just see what happens.

Moreover, we can also see the finite dimensional representations of this algebra $\mathbb{C} Q $. Up to isomorphism they are all of the following form : at each vertex $v_i $ of the quiver one places a finite dimensional vectorspace $\mathbb{C}^{d_i} $ and any arrow in the quiver
[tex]\xymatrix{\vtx{v_i} \ar[r]^a & \vtx{v_j}}[/tex] determines a linear map between these vertex spaces, that is, to $a $ corresponds a matrix in $M_{d_j \times d_i}(\mathbb{C}) $. These matrices determine how the paths of length one act on the representation, longer paths act via multiplcation of matrices along the oriented path.

A necklace in the quiver is a closed oriented path in the quiver up to cyclic permutation of the arrows making up the cycle. That is, we are free to choose the start (and end) point of the cycle. For example, in the one-cycle quiver

[tex]\xymatrix{\vtx{} \ar[rr]^a & & \vtx{} \ar[ld]^b \\ & \vtx{} \ar[lu]^c &}[/tex]

the basic necklace can be represented as $abc $ or $bca $ or $cab $. How does a necklace act on a representation? Well, the matrix-multiplication of the matrices corresponding to the arrows gives a square matrix in each of the vertices in the cycle. Though the dimensions of this matrix may vary from vertex to vertex, what does not change (and hence is a property of the necklace rather than of the particular choice of cycle) is the trace of this matrix. That is, necklaces give complex-valued functions on representations of $\mathbb{C} Q $ and by a result of Artin and Procesi there are enough of them to distinguish isoclasses of (semi)simple representations! That is, linear combinations a necklaces (aka super-potentials) can be viewed, after taking traces, as complex-valued functions on all representations (similar to character-functions).

In physics, one views these functions as potentials and it then interested in the points (representations) where this function is extremal (minimal) : the vacua. Clearly, this does not make much sense in the complex-case but is relevant when we look at the real-case (where we look at skew-Hermitian matrices rather than all matrices). A motivating example (the Yang-Mills potential) is given in Example 2.3.2 of Victor Ginzburg’s paper Calabi-Yau algebras.

Let $\Phi $ be a super-potential (again, a linear combination of necklaces) then our commutative intuition tells us that extrema correspond to zeroes of all partial differentials $\frac{\partial \Phi}{\partial a} $ where $a $ runs over all coordinates (in our case, the arrows of the quiver). One can make sense of differentials of necklaces (and super-potentials) as follows : the partial differential with respect to an arrow $a $ occurring in a term of $\Phi $ is defined to be the path in the quiver one obtains by removing all 1-occurrences of $a $ in the necklaces (defining $\Phi $) and rearranging terms to get a maximal broken necklace (using the cyclic property of necklaces). An example, for the cyclic quiver above let us take as super-potential $abcabc $ (2 cyclic turns), then for example

$\frac{\partial \Phi}{\partial b} = cabca+cabca = 2 cabca $

(the first term corresponds to the first occurrence of $b $, the second to the second). Okay, but then the vacua-representations will be the representations of the quotient-algebra (which I like to call the vacualgebra)

$\mathcal{U}(Q,\Phi) = \frac{\mathbb{C} Q}{(\partial \Phi/\partial a, \forall a)} $

which in ‘physical relevant settings’ (whatever that means…) turn out to be Calabi-Yau algebras.

But, let us return to the case of subgroups of the modular group and their quivers. Do we have a natural super-potential in this case? Well yes, the quiver encoded a triangulation of the compactification of $\mathbb{H}/\Lambda $ and if we choose an orientation it turns out that all ‘black’ triangles (with respect to the Dedekind tessellation) have their arrow-sides defining a necklace, whereas for the ‘white’ triangles the reverse orientation makes the arrow-sides into a necklace. Hence, it makes sense to look at the cubic superpotential $\Phi $ being the sum over all triangle-sides-necklaces with a +1-coefficient for the black triangles and a -1-coefficient for the white ones. Let’s consider an index three example from a previous post

[tex]\xymatrix{& & \rho \ar[lld]_d \ar[ld]^f \ar[rd]^e & \\
i \ar[rrd]_a & i+1 \ar[rd]^b & & \omega \ar[ld]^c \\
& & 0 \ar[uu]^h \ar@/^/[uu]^g \ar@/_/[uu]_i &}[/tex]

In this case the super-potential coming from the triangulation is

$\Phi = -aid+agd-cge+che-bhf+bif $

and therefore we have a noncommutative algebra $\mathcal{U}(Q,\Phi) $ associated to this index 3 subgroup. Contrary to what I believed at the start of this series, the algebras one obtains in this way from dessins d’enfants are far from being Calabi-Yau (in whatever definition). For example, using a GAP-program written by Raf Bocklandt Ive checked that the growth rate of the above algebra is similar to that of $\mathbb{C}[x] $, so in this case $\mathcal{U}(Q,\Phi) $ can be viewed as a noncommutative curve (with singularities).

However, this is not the case for all such algebras. For example, the vacualgebra associated to the second index three subgroup (whose fundamental domain and quiver were depicted at the end of this post) has growth rate similar to that of $\mathbb{C} \langle x,y \rangle $…

I have an outlandish conjecture about the growth-behavior of all algebras $\mathcal{U}(Q,\Phi) $ coming from dessins d’enfants : the algebra sees what the monodromy representation of the dessin sees of the modular group (or of the third braid group).
I can make this more precise, but perhaps it is wiser to calculate one or two further examples…

One Comment

Vacation reading

Published July 26, 2007 by lievenlb

Im in the process of writing/revising/extending the course notes for next year and will therefore pack more math-books than normal.

These are for a 3rd year Bachelor course on Algebraic Geometry and a 1st year Master course on Algebraic and Differential Geometry. The bachelor course was based this year partly on Miles Reid’s Undergraduate Algebraic Geometry and partly on David Mumford’s Red Book, but this turned out to be too heavy going. Next year I’ll be happy if they know enough on algebraic curves. The backbone of these two courses will be Fulton’s old but excellent Algebraic curves. It’s self contained (unlike Hartshorne’s book that assumes a prior course on commutative algebra), contains a lot of exercises and goes on to the Brill-Noether proof of Riemann-Roch. Still, Id like to extend it with the introductory chapter and the chapters on Riemann surfaces from Complex Algebraic Curves by Frances Kirwan, a bit on elliptic and modular functions from Elliptic curves by Henry McKean and Victor Moll and the adelic proof of Riemann-Roch and applications of it to the construction of algebraic codes from Algebraic curves over finite fields by Carlos Moreno. If time allows Id love to include also the chapter on zeta functions but I fear this will be difficult.

These are to spice up a 2nd year Bachelor course on Representations of Finite Groups with a tiny bit of Galois representations, both as motivation and to wet their appetite for elliptic curves and algebraic geometry. Ive received Fearless Symmetry by Avner Ash and Robert Gross only yesterday and find it hard to stop reading. It attempts to explain Galois representations and generalized reciprocity laws to a general audience and from what I read so far, they really do a terrific job. Another excellent elementary introduction to elliptic curves and Galois representations is in Invitation to the Mathematics of Fermat-Wiles by Yves Hellegouarch. On a gossipy note, the appendix “The origin of the elliptic approach to Fermat’s last theorem” is fun reading. Finally, Ill also take Introduction to Fermat’s Last Theorem by Alf van der Poorten along simply because I love his writing style.

These are included just for fun. The Poincare Conjecture by Donal O’Shea because I know far too little about it, Letters to a Young Mathematician by Ian Stewart because I like the concept of the book and finally The sensual (quadratic) form by John Conway because I need to have at all times at least one Conway-book nearby.

4 Comments