Tag: Dedekind

Farey symbols of sporadic groups

Published March 20, 2008 by lievenlb

John Conway once wrote :

There are almost as many different constructions of $M_{24} $ as there have been mathematicians interested in that most remarkable of all finite groups.

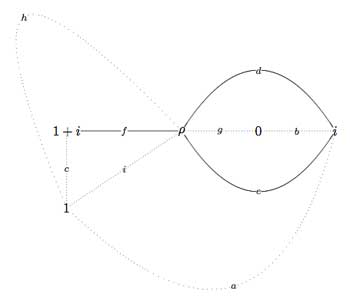
In the inguanodon post Ive added yet another construction of the Mathieu groups $M_{12} $ and $M_{24} $ starting from (half of) the Farey sequences and the associated cuboid tree diagram obtained by demanding that all edges are odd. In this way the Mathieu groups turned out to be part of a (conjecturally) infinite sequence of simple groups, starting as follows :

$L_2(7),M_{12},A_{16},M_{24},A_{28},A_{40},A_{48},A_{60},A_{68},A_{88},A_{96},A_{120},A_{132},A_{148},A_{164},A_{196},\ldots $

It is quite easy to show that none of the other sporadics will appear in this sequence via their known permutation representations. Still, several of the sporadic simple groups are generated by an element of order two and one of order three, so they are determined by a finite dimensional permutation representation of the modular group $PSL_2(\mathbb{Z}) $ and hence are hiding in a special polygonal region of the Dedekind’s tessellation

Let us try to figure out where the sporadic with the next simplest permutation representation is hiding : the second Janko group $J_2 $, via its 100-dimensional permutation representation. The Atlas tells us that the order two and three generators act as

e:= (1,84)(2,20)(3,48)(4,56)(5,82)(6,67)(7,55)(8,41)(9,35)(10,40)(11,78)(12, 100)(13,49)(14,37)(15,94)(16,76)(17,19)(18,44)(21,34)(22,85)(23,92)(24, 57)(25,75)(26,28)(27,64)(29,90)(30,97)(31,38)(32,68)(33,69)(36,53)(39,61) (42,73)(43,91)(45,86)(46,81)(47,89)(50,93)(51,96)(52,72)(54,74)(58,99) (59,95)(60,63)(62,83)(65,70)(66,88)(71,87)(77,98)(79,80);

v:= (1,80,22)(2,9,11)(3,53,87)(4,23,78)(5,51,18)(6,37,24)(8,27,60)(10,62,47) (12,65,31)(13,64,19)(14,61,52)(15,98,25)(16,73,32)(17,39,33)(20,97,58) (21,96,67)(26,93,99)(28,57,35)(29,71,55)(30,69,45)(34,86,82)(38,59,94) (40,43,91)(42,68,44)(46,85,89)(48,76,90)(49,92,77)(50,66,88)(54,95,56) (63,74,72)(70,81,75)(79,100,83);

But as the kfarey.sage package written by Chris Kurth calculates the Farey symbol using the L-R generators, we use GAP to find those

L = e*v^-1  and  R=e*v^-2 so

L=(1,84,22,46,70,12,79)(2,58,93,88,50,26,35)(3,90,55,7,71,53,36)(4,95,38,65,75,98,92)(5,86,69,39,14,6,96)(8,41,60,72,61,17, 64)(9,57,37,52,74,56,78)(10,91,40,47,85,80,83)(11,23,49,19,33,30,20)(13,77,15,59,54,63,27)(16,48,87,29,76,32,42)(18,68, 73,44,51,21,82)(24,28,99,97,45,34,67)(25,81,89,62,100,31,94)

R=(1,84,80,100,65,81,85)(2,97,69,17,13,92,78)(3,76,73,68,16,90,71)(4,54,72,14,24,35,11)(5,34,96,18,42,32,44)(6,21,86,30,58, 26,57)(7,29,48,53,36,87,55)(8,41,27,19,39,52,63)(9,28,93,66,50,99,20)(10,43,40,62,79,22,89)(12,83,47,46,75,15,38)(23,77, 25,70,31,59,56)(33,45,82,51,67,37,61)(49,64,60,74,95,94,98)

Defining these permutations in sage and using kfarey, this gives us the Farey-symbol of the associated permutation representation

L=SymmetricGroup(Integer(100))("(1,84,22,46,70,12,79)(2,58,93,88,50,26,35)(3,90,55,7,71,53,36)(4,95,38,65,75,98,92)(5,86,69,39,14,6,96)(8,41,60,72,61,17, 64)(9,57,37,52,74,56,78)(10,91,40,47,85,80,83)(11,23,49,19,33,30,20)(13,77,15,59,54,63,27)(16,48,87,29,76,32,42)(18,68, 73,44,51,21,82)(24,28,99,97,45,34,67)(25,81,89,62,100,31,94)")

R=SymmetricGroup(Integer(100))("(1,84,80,100,65,81,85)(2,97,69,17,13,92,78)(3,76,73,68,16,90,71)(4,54,72,14,24,35,11)(5,34,96,18,42,32,44)(6,21,86,30,58, 26,57)(7,29,48,53,36,87,55)(8,41,27,19,39,52,63)(9,28,93,66,50,99,20)(10,43,40,62,79,22,89)(12,83,47,46,75,15,38)(23,77, 25,70,31,59,56)(33,45,82,51,67,37,61)(49,64,60,74,95,94,98)")

sage: FareySymbol("Perm",[L,R])

[[0, 1, 4, 3, 2, 5, 18, 13, 21, 71, 121, 413, 292, 463, 171, 50, 29, 8, 27, 46, 65, 19, 30, 11, 3, 10, 37, 64, 27, 17, 7, 4, 5], [1, 1, 3, 2, 1, 2, 7, 5, 8, 27, 46, 157, 111, 176, 65, 19, 11, 3, 10, 17, 24, 7, 11, 4, 1, 3, 11, 19, 8, 5, 2, 1, 1], [-3, 1, 4, 4, 2, 3, 6, -3, 7, 13, 14, 15, -3, -3, 15, 14, 11, 8, 8, 10, 12, 12, 10, 9, 5, 5, 9, 11, 13, 7, 6, 3, 2, 1]]

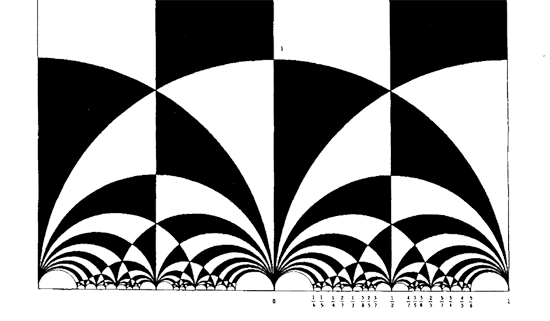
Here, the first string gives the numerators of the cusps, the second the denominators and the third gives the pairing information (where [tex[-2 $ denotes an even edge and $-3 $ an odd edge. Fortunately, kfarey also allows us to draw the special polygonal region determined by a Farey-symbol. So, here it is (without the pairing data) :

the hiding place of $J_2 $…

It would be nice to have (a) other Farey-symbols associated to the second Janko group, hopefully showing a pattern that one can extend into an infinite family as in the inguanodon series and (b) to determine Farey-symbols of more sporadic groups.

Quiver-superpotentials

Published January 14, 2008 by lievenlb

It’s been a while, so let’s include a recap : a (transitive) permutation representation of the modular group $\Gamma = PSL_2(\mathbb{Z}) $ is determined by the conjugacy class of a cofinite subgroup $\Lambda \subset \Gamma $, or equivalently, to a dessin d’enfant. We have introduced a quiver (aka an oriented graph) which comes from a triangulation of the compactification of $\mathbb{H} / \Lambda $ where $\mathbb{H} $ is the hyperbolic upper half-plane. This quiver is independent of the chosen embedding of the dessin in the Dedeking tessellation. (For more on these terms and constructions, please consult the series Modular subgroups and Dessins d’enfants).

Why are quivers useful? To start, any quiver $Q $ defines a noncommutative algebra, the path algebra $\mathbb{C} Q $, which has as a $\mathbb{C} $-basis all oriented paths in the quiver and multiplication is induced by concatenation of paths (when possible, or zero otherwise). Usually, it is quite hard to make actual computations in noncommutative algebras, but in the case of path algebras you can just see what happens.

Moreover, we can also see the finite dimensional representations of this algebra $\mathbb{C} Q $. Up to isomorphism they are all of the following form : at each vertex $v_i $ of the quiver one places a finite dimensional vectorspace $\mathbb{C}^{d_i} $ and any arrow in the quiver
[tex]\xymatrix{\vtx{v_i} \ar[r]^a & \vtx{v_j}}[/tex] determines a linear map between these vertex spaces, that is, to $a $ corresponds a matrix in $M_{d_j \times d_i}(\mathbb{C}) $. These matrices determine how the paths of length one act on the representation, longer paths act via multiplcation of matrices along the oriented path.

A necklace in the quiver is a closed oriented path in the quiver up to cyclic permutation of the arrows making up the cycle. That is, we are free to choose the start (and end) point of the cycle. For example, in the one-cycle quiver

[tex]\xymatrix{\vtx{} \ar[rr]^a & & \vtx{} \ar[ld]^b \\ & \vtx{} \ar[lu]^c &}[/tex]

the basic necklace can be represented as $abc $ or $bca $ or $cab $. How does a necklace act on a representation? Well, the matrix-multiplication of the matrices corresponding to the arrows gives a square matrix in each of the vertices in the cycle. Though the dimensions of this matrix may vary from vertex to vertex, what does not change (and hence is a property of the necklace rather than of the particular choice of cycle) is the trace of this matrix. That is, necklaces give complex-valued functions on representations of $\mathbb{C} Q $ and by a result of Artin and Procesi there are enough of them to distinguish isoclasses of (semi)simple representations! That is, linear combinations a necklaces (aka super-potentials) can be viewed, after taking traces, as complex-valued functions on all representations (similar to character-functions).

In physics, one views these functions as potentials and it then interested in the points (representations) where this function is extremal (minimal) : the vacua. Clearly, this does not make much sense in the complex-case but is relevant when we look at the real-case (where we look at skew-Hermitian matrices rather than all matrices). A motivating example (the Yang-Mills potential) is given in Example 2.3.2 of Victor Ginzburg’s paper Calabi-Yau algebras.

Let $\Phi $ be a super-potential (again, a linear combination of necklaces) then our commutative intuition tells us that extrema correspond to zeroes of all partial differentials $\frac{\partial \Phi}{\partial a} $ where $a $ runs over all coordinates (in our case, the arrows of the quiver). One can make sense of differentials of necklaces (and super-potentials) as follows : the partial differential with respect to an arrow $a $ occurring in a term of $\Phi $ is defined to be the path in the quiver one obtains by removing all 1-occurrences of $a $ in the necklaces (defining $\Phi $) and rearranging terms to get a maximal broken necklace (using the cyclic property of necklaces). An example, for the cyclic quiver above let us take as super-potential $abcabc $ (2 cyclic turns), then for example

$\frac{\partial \Phi}{\partial b} = cabca+cabca = 2 cabca $

(the first term corresponds to the first occurrence of $b $, the second to the second). Okay, but then the vacua-representations will be the representations of the quotient-algebra (which I like to call the vacualgebra)

$\mathcal{U}(Q,\Phi) = \frac{\mathbb{C} Q}{(\partial \Phi/\partial a, \forall a)} $

which in ‘physical relevant settings’ (whatever that means…) turn out to be Calabi-Yau algebras.

But, let us return to the case of subgroups of the modular group and their quivers. Do we have a natural super-potential in this case? Well yes, the quiver encoded a triangulation of the compactification of $\mathbb{H}/\Lambda $ and if we choose an orientation it turns out that all ‘black’ triangles (with respect to the Dedekind tessellation) have their arrow-sides defining a necklace, whereas for the ‘white’ triangles the reverse orientation makes the arrow-sides into a necklace. Hence, it makes sense to look at the cubic superpotential $\Phi $ being the sum over all triangle-sides-necklaces with a +1-coefficient for the black triangles and a -1-coefficient for the white ones. Let’s consider an index three example from a previous post

[tex]\xymatrix{& & \rho \ar[lld]_d \ar[ld]^f \ar[rd]^e & \\
i \ar[rrd]_a & i+1 \ar[rd]^b & & \omega \ar[ld]^c \\
& & 0 \ar[uu]^h \ar@/^/[uu]^g \ar@/_/[uu]_i &}[/tex]

In this case the super-potential coming from the triangulation is

$\Phi = -aid+agd-cge+che-bhf+bif $

and therefore we have a noncommutative algebra $\mathcal{U}(Q,\Phi) $ associated to this index 3 subgroup. Contrary to what I believed at the start of this series, the algebras one obtains in this way from dessins d’enfants are far from being Calabi-Yau (in whatever definition). For example, using a GAP-program written by Raf Bocklandt Ive checked that the growth rate of the above algebra is similar to that of $\mathbb{C}[x] $, so in this case $\mathcal{U}(Q,\Phi) $ can be viewed as a noncommutative curve (with singularities).

However, this is not the case for all such algebras. For example, the vacualgebra associated to the second index three subgroup (whose fundamental domain and quiver were depicted at the end of this post) has growth rate similar to that of $\mathbb{C} \langle x,y \rangle $…

I have an outlandish conjecture about the growth-behavior of all algebras $\mathcal{U}(Q,\Phi) $ coming from dessins d’enfants : the algebra sees what the monodromy representation of the dessin sees of the modular group (or of the third braid group).
I can make this more precise, but perhaps it is wiser to calculate one or two further examples…

One Comment

quivers versus quilts

Published January 2, 2008 by lievenlb

We have associated to a subgroup of the modular group $PSL_2(\mathbb{Z}) $ a quiver (that is, an oriented graph). For example, one verifies that the fundamental domain of the subgroup $\Gamma_0(2) $ (an index 3 subgroup) is depicted on the right by the region between the thick lines with the identification of edges as indicated. The associated quiver is then

\[
\xymatrix{i \ar[rr]^a \ar[dd]^b & & 1 \ar@/^/[ld]^h \ar@/_/[ld]_i \\
& \rho \ar@/^/[lu]^d \ar@/_/[lu]_e \ar[rd]^f & \\
0 \ar[ru]^g & & i+1 \ar[uu]^c}
\]

The corresponding “dessin d’enfant” are the green edges in the picture. But, the red dot on the left boundary is identied with the red dot on the lower circular boundary, so the dessin of the modular subgroup $\Gamma_0(2) $ is

\[
\xymatrix{| \ar@{-}[r] & \bullet \ar@{-}@/^8ex/[r] \ar@{-}@/_8ex/[r] & -}
\]

Here, the three red dots (all of them even points in the Dedekind tessellation) give (after the identification) the two points indicated by a $\mid $ whereas the blue dot (an odd point in the tessellation) is depicted by a $\bullet $. There is another ‘quiver-like’ picture associated to this dessin, a quilt of the modular subgroup $\Gamma_0(2) $ as studied by John Conway and Tim Hsu.

On the left, a quilt-diagram copied from Hsu’s book Quilts : central extensions, braid actions, and finite groups, exercise 3.3.9. This ‘quiver’ has also 5 vertices and 7 arrows as our quiver above, so is there a connection?

A quilt is a gadget to study transitive permutation representations of the braid group $B_3 $ (rather than its quotient, the modular group $PSL_2(\mathbb{Z}) = B_3/\langle Z \rangle $ where $\langle Z \rangle $ is the cyclic center of $B_3 $. The $Z $-stabilizer subgroup of all elements in a transitive permutation representation of $B_3 $ is the same and hence of the form $\langle Z^M \rangle $ where M is called the modulus of the representation. The arrow-data of a quilt, that is the direction of certain edges and their labeling with numbers from $\mathbb{Z}/M \mathbb{Z} $ (which have to satisfy some requirements, the flow rules, but more about that another time) encode the Z-action on the permutation representation. The dimension of the representation is $M \times k $ where $k $ is the number of half-edges in the dessin. In the above example, the modulus is 5 and the dessin has 3 (half)edges, so it depicts a 15-dimensional permutation representation of $B_3 $.

If we forget the Z-action (that is, the arrow information), we get a permutation representation of the modular group (that is a dessin). So, if we delete the labels and directions on the edges we get what Hsu calls a modular quilt, that is, a picture consisting of thick edges (the dessin) together with dotted edges which are called the seams of the modular quilt. The modular quilt is merely another way to depict a fundamental domain of the corresponding subgroup of the modular group. 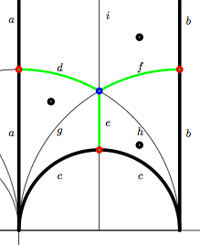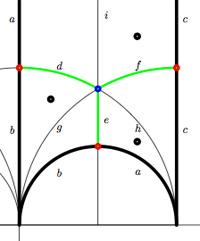For the above example, we have the indicated correspondences between the fundamental domain of $\Gamma_0(2) $ in the upper half-plane (on the left) and as a modular quilt (on the right)

That is, we can also get our quiver (or its opposite quiver) from the modular quilt by fixing the orientation of one 2-cell. For example, if we fix the orientation of the 2-cell $\vec{fch} $ we get our quiver back from the modular quilt

\[
\xymatrix{i \ar[rr]^a \ar[dd]^b & & 1 \ar@/^/[ld]^h \ar@/_/[ld]_i \\
& \rho \ar@/^/[lu]^d \ar@/_/[lu]_e \ar[rd]^f & \\
0 \ar[ru]^g & & i+1 \ar[uu]^c}
\]

This shows that the quiver (or its opposite) associated to a (conjugacy class of a) subgroup of $PSL_2(\mathbb{Z}) $ does not depend on the choice of embedding of the dessin (or associated cuboid tree diagram) in the upper half-plane. For, one can get the modular quilt from the dessin by adding one extra vertex for every connected component of the complement of the dessin (in the example, the two vertices corresponding to 0 and 1) and drawing a triangulation from them (the dotted lines or ‘seams’).

One Comment