Cameron – neverendingbooks

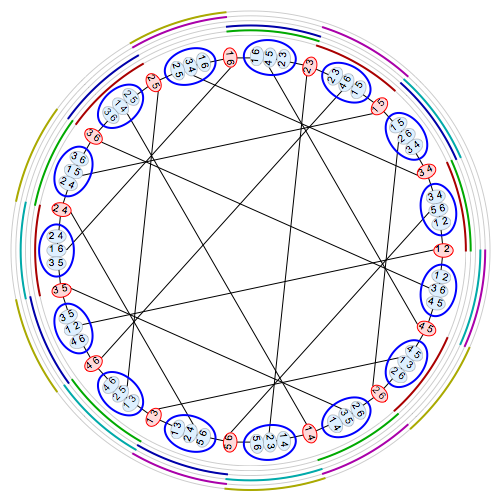
Here’s a nice, symmetric, labeled graph:

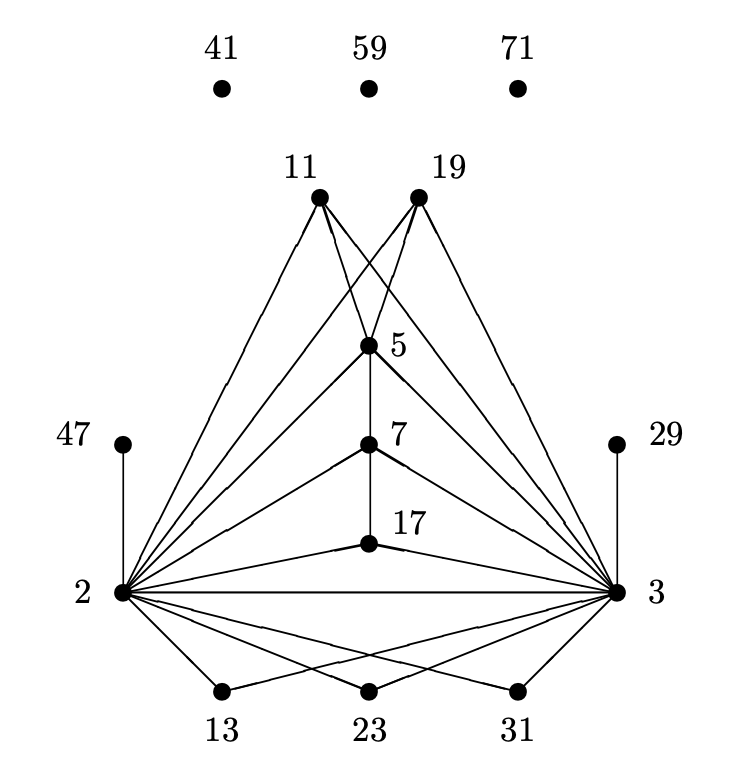
The prime numbers labelling the vertices are exactly the prime divisors of the order of the largest sporadic group: the monster group $\mathbb{M}$.
\[
\# \mathbb{M} = 2^{46}.3^{20}.5^9.7^6.11^2.13^3.17.19.23.29.31.41.47.59.71 \]

Looking (for example) at the character table of the monster you can check that there is an edge between two primes $p$ and $q$ exactly when the monster has an element of order $p.q$.

Now the fun part: this graph characterises the Monster!

There is no other group $G$ having only elements of these prime orders, and only these edges for its elements of order $p.q$.

This was proved by Melissa Lee and Tomasz Popiel in $\mathbb{M}, \mathbb{B}$, and $\mathbf{Co}_1$ are recognisable by their prime graphs, by using modular character theory.

The proof for the Monster takes less than one page, so it’s clear that it builds on lots of previous results.

There’s the work of Mina Hagie The prime graph of a sporadic simple group, who used the classification of all finite simple groups to put heavy restrictions on possible groups $G$ having the same prime graph as a sporadic simple group.

For the Monster, she proved that if the prime graph of $G$ is that of the monster, then the Fitting subgroup $F(G)$ must be a $3$-group, and $G/F(G) \simeq \mathbb{M}$.

Her result, in turn, builds on the Gruenberg-Kegel theorem, after Karl Gruenberg and Otto Kegel.

The Gruenberg-Kegel theorem, which they never published (a write-up is in the paper Prime graph components of finite groups by Williams), shows the wealth of information contained in the prime graph of a finite group. For this reason, the prime graph is often called the Gruenberg-Kegel graph.

The pictures above are taken from a talk by Peter Cameron, The Gruenberg-Kegel graph. Peter Cameron’s blog is an excellent source of information for all things relating groups and graphs.

The full proof of the Gruenberg-Kegel theorem is way too involved for a blogpost, but I should give you at least an idea of it, and of one of the recurrent tools involved, the structural results on Frobenius groups by John Thompson.

Here’s lemma 1.1 of the paper On connection between the structure of a finite group and the properties of its prime graph by A.V. Vasil’ev.

Lemma: If $1 \triangleleft K \triangleleft H \triangleleft G$ is a series of normal subgroups, and if we have primes $p$ dividing the order of $K$, $q$ dividing the order of $H/K$, and $r$ dividing the order of $G/H$, then there is at least one edge among these three vertices in the prime graph of $G$.

Okay, let’s suppose there’s a counterexample $G$, and take one of minimal order. Let $P$ be a Sylow $p$-subgroup of $K$, and $N$ its normaliser in $G$. By the Frattini argument $G=K.N$ and so $G/K \simeq N/(N \cap K)$.

Then there’s a normal series $1 \triangleleft P \triangleleft (N \cap H)=N_H(P) \triangleleft N$, and by Frattini $H=K.(N \cap H)$. But then, $N/(N \cap H)=H.N/H = G/H$ and $(N \cap H)/P$ maps onto $(N \cap H)/(N \cap H \cap K) = H/K$, so this series satisfies the conditions for the three primes $p,q$ and $r$.

But as there is no edge among $p,q$ and $r$ in the prime graph of $G$, there can be no such edge in the prime graph of $N$, and $N$ would be a counterexample of smaller order, unless $N=G$.

Oh, I should have said this before: if there is an edge between two primes in the prime graph of a subgroup (or a quotient) of $G$, then such as edge exists also in the prime group of $G$ (trivial for subgroups, use lifts of elements for quotients).

The only way out is that $N=G$, or that $P$ is a normal subgroup of $G$. Look at quotients $\overline{G}=G/P$ and $\overline{H}=H/P$, take a Sylow $q$-subgroup of $\overline{H}$ and $\overline{M}$ its normaliser in $\overline{G}$.

Frattini again gives $\overline{M}/(\overline{M} \cap \overline{H}) = \overline{G}/\overline{H}$, and $r$ is a prime divisor of the order of $\overline{M}/\overline{Q}$.

Lift the whole schmuck to the lift of $\overline{M}$ in $G$ and get a series of normal subgroups
\[
1 \triangleleft P \triangleleft Q \triangleleft M \]
satisfying the three primes condition, so would give a smaller counter-example unless $M=G$ and $Q$ (the lift of $\overline{Q}$ to $G$) is a normal subgroup of $G$.

Sooner or later, in almost all proofs around the Gruenberg-Kegel result, a Frobenius group enters the picture.

Here, we take an element $x$ in $G$ of order $r$, and consider the subgroup $F$ generated by $Q$ and $x$. The action of $x$ on $Q$ by conjugation is fixed-point free (if not, $G$ would have elements of order $p.r$ or $q.r$ and there is no edge between these prime vertices by assumption).

But then, $F$ is a semi-direct product $Q \rtimes \langle x \rangle$, and again because $G$ has no elements of order $p.r$ nor $q.r$ we have:

the centraliser-subgroup in $F$ of any non-identity element in $\langle x \rangle$ is contained in $\langle x \rangle$
the centraliser-subgroup in $F$ of any non-identity element in $Q$ is contained in $Q$

So, $F$ is a Frobenius group with ‘Frobenius kernel’ $Q$. Thompson proved that the Frobenius kernel is a nilpotent group, so a product of its Sylow-subgroups. But then, $Q$ (and therefore $G$) contains an element of order $p.q$, done.

Leave a Comment

I was running a bachelor course on representations of finite groups and a master course on simple (mainly sporadic) groups until Corona closed us down. Perhaps these blog-posts can be useful to some.

A curious fact, with ripple effect on Mathieu sporadic groups, is that the symmetric group $S_6$ has an automorphism $\phi$, different from an automorphism by conjugation.

In the course notes the standard approach was given, based on the $5$-Sylow subgroups of $S_5$.

Here’s the idea. Let $S_6$ act by permuting $6$ elements and consider the subgroup $S_5$ fixing say $6$. If such an odd automorphism $\phi$ would exist, then the subgroup $\phi(S_5)$ cannot fix one of the six elements (for then it would be conjugated to $S_5$), so it must act transitively on the six elements.

The alternating group $A_5$ is the rotation symmetry group of the icosahedron

Any $5$-Sylow subgroup of $A_5$ is the cyclic group $C_5$ generated by a rotation among one of the six body-diagonals of the icosahedron. As $A_5$ is normal in $S_5$, also $S_5$ has six $5$-Sylows.

More lowbrow, such a subgroup is generated by a permutation of the form $(1,2,a,b,c)$, of which there are six. Good old Sylow tells us that these $5$-Sylow subgroups are conjugated, giving a monomorphism
\[
S_5 \rightarrow Sym(\{ 5-Sylows \})\simeq S_6 \]
and its image $H$ is a subgroup of $S_6$ of index $6$ (and isomorphic to $S_5$) which acts transitively on six elements.

Left multiplication gives an action of $S_6$ on the six cosets $S_6/H =\{ \sigma H~:~\sigma \in S_6 \}$, that is a groupmorphism
\[
\phi : S_6 \rightarrow Sym(\{ \sigma H \}) = S_6 \]
which is our odd automorphism (actually it is even, of order two). A calculation shows that $\phi$ sends permutations of cycle shape $2.1^4$ to shape $2^3$, so can’t be given by conjugation (which preserves cycle shapes).

An alternative approach is given by Noah Snyder in an old post at the Secret Blogging Seminar.

Here, we like to identify the six points $\{ a,b,c,d,e,f \}$ with the six points $\{ 0,1,2,3,4,\infty \}$ of the projective line $\mathbb{P}^1(\mathbb{F}_5)$ over the finite field $\mathbb{F}_5$.

There are $6!$ different ways to do this set-theoretically, but lots of them are the same up to an automorphism of $\mathbb{P}^1(\mathbb{F}_5)$, that is an element of $PGL_2(\mathbb{F}_5)$ acting via Mobius transformations on $\mathbb{P}^1(\mathbb{F}_5)$.

$PGL_2(\mathbb{F}_5)$ acts $3$-transitively on $\mathbb{P}^1(\mathbb{F}_5)$ so we can fix three elements in each class, say $a=0,b=1$ and $f=\infty$, leaving six different ways to label the points of the projective line
\[
\begin{array}{c|cccccc}
& a & b & c & d & e & f \\
\hline
1 & 0 & 1 & 2 & 3 & 4 & \infty \\
2 & 0 & 1 & 2 & 4 & 3 & \infty \\
3 & 0 & 1 & 3 & 2 & 4 & \infty \\
4 & 0 & 1 & 3 & 4 & 2 & \infty \\
5 & 0 & 1 & 4 & 2 & 3 & \infty \\
6 & 0 & 1 & 4 & 3 & 2 & \infty
\end{array}
\]
A permutation of the six elements $\{ a,b,c,d,e,f \}$ will result in a permutation of the six classes of $\mathbb{P}^1(\mathbb{F}_5)$-labelings giving the odd automorphism
\[
\phi : S_6 = Sym(\{ a,b,c,d,e,f \}) \rightarrow Sym(\{ 1,2,3,4,5,6 \}) = S_6 \]
An example: the involution $(a,b)$ swaps the points $0$ and $1$ in $\mathbb{P}^1(\mathbb{F}_5)$, which can be corrected via the Mobius-automorphism $t \mapsto 1-t$. But this automorphism has an effect on the remaining points
\[
2 \leftrightarrow 4 \qquad 3 \leftrightarrow 3 \qquad \infty \leftrightarrow \infty \]
So the six different $\mathbb{P}^1(\mathbb{F}_5)$ labelings are permuted as
\[
\phi((a,b))=(1,6)(2,5)(3,4) \]
showing (again) that $\phi$ is not a conjugation-automorphism.

Yet another, and in fact the original, approach by James Sylvester uses the strange terminology of duads, synthemes and synthematic totals.

A duad is a $2$-element subset of $\{ 1,2,3,4,5,6 \}$ (there are $15$ of them).
A syntheme is a partition of $\{ 1,2,3,4,5,6 \}$ into three duads (there are $15$ of them).
A (synthematic) total is a partition of the $15$ duads into $5$ synthemes, and they are harder to count.

There’s a nice blog-post by Peter Cameron on this, as well as his paper From $M_{12}$ to $M_{24}$ (after Graham Higman). As my master-students have to work their own way through this paper I will not spoil their fun in trying to deduce that

Two totals have exactly one syntheme in common, so synthemes are ‘duads of totals’.
Three synthemes lying in disjoint pairs of totals must consist of synthemes containing a fixed duad, so duads are ‘synthemes of totals’.
Duads come from disjoint synthemes of totals in this way if and only if they share a point, so points are ‘totals of totals’

My hint to the students was “Google for John Baez+six”, hoping they’ll discover Baez’ marvellous post Some thoughts on the number $6$, and in particular, the image (due to Greg Egan) in that post

which makes everything visually clear.

The duads are the $15$ red vertices, the synthemes the $15$ blue vertices, connected by edges when a duad is contained in a syntheme. One obtains the Tutte-Coxeter graph.

The $6$ concentric rings around the picture are the $6$ synthematic totals. A band of color appears in one of these rings near some syntheme if that syntheme is part of that synthematic total.

If $\{ t_1,t_2,t_3,t_4,t_5,t_6 \}$ are the six totals, then any permutation $\sigma$ of $\{ 1,2,3,4,5,6 \}$ induces a permutation $\phi(\sigma)$ of the totals, giving the odd automorphism
\[
\phi : S_6 = Sym(\{ 1,2,3,4,5,6 \}) \rightarrow Sym(\{ t_1,t_2,t_3,t_4,t_5,t_6 \}) = S_6 \]

Tag: Cameron

The monster prime graph

Sylvester’s synthemes