Skip to content →

Tag: blogging

mathblogging and poll-results

Published January 21, 2011 by lievenlb

Mathblogging.org is a recent initiative and may well become the default starting place to check on the status of the mathematical blogosphere.

Handy, if you want to (re)populate your RSS-aggregator with interesting mathematical blogs, is their graphical presentation of (nearly) all math-blogs ordered by type : group blogs, individual researchers, teachers and educators, journalistic writers, communities, institutions and microblogging (twitter). Links to the last 7 posts are given so you can easily determine whether that particular blog is of interest to you.

The three people behind the project, Felix Breuer, Frederik von Heymann and Peter Krautzberger, welcome you to send them links to (micro)blogs they’ve missed. Surely, there must be a lot more mathematicians with a twitter-account than the few ones listed so far…

Even more convenient is their list of latest posts from their collection, ordered by date. I’ve put that page in my Bookmarks Bar the moment I discovered it! It would be nice, if they could provide an RSS-feed of this list, so that people could place it in their sidebar, replacing old-fashioned and useless blogrolls. The site does provide two feeds, but they are completely useless as they click through to empty pages…

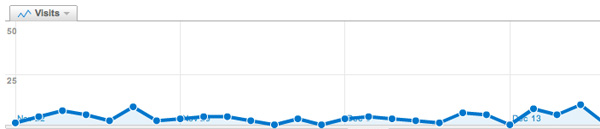
While we’re on the topic of math-blogging, the results of the ‘What should we write about next?’-poll that ran the previous two days on the entry page. Of all people visiting that page, 2.6% left suggestions.

The vast majority (67%) wants more posts on noncommutative geometry. Most of you are craving for introductions (and motivation) accessible to undergraduates (as ‘it’s hard to find quality, updated information on this’). In particular, you want posts giving applications in mathematics (especially number theory), or explaining relationships between different approaches. One person knew exactly how I should go about to achieve the hoped-for accessibility : “As a rule, I’d take what you think would be just right for undergrads, and then trim it down a little more.”

Others want rather specialized posts, such as on ‘connection and parallel transport in noncommutative geometry’ or on ‘trees (per J-L. Loday, M. Aguiar, Connes/Kreimer renormalization (aka Butcher group)), or something completely other tree-related’.

Fortunately, some of you told me it was fine to write about ‘combinatorial games and cool nim stuff, finite simple groups, mathematical history, number theory, arithmetic geometry’, pushed me to go for ‘anything monstrous and moonshiney’ (as if I would know the secrets of the ‘connection between the Mathieu group M24 and the elliptic genus of K3’…) or wrote that ‘various algebraic geometry related posts are always welcome: posts like Mumford’s treasure map‘.

5 Comments

NeB : 7 years and now an iPad App

Published December 31, 2010 by lievenlb

Exactly 7 years ago I wrote my first post. This blog wasn’t called NeB yet and it used pMachine, a then free blogging tool (later transformed into expression engine), rather than WordPress.

Over the years NeB survived three hardware-upgrades of ‘the Matrix’ (the webserver hosting it), more themes than I care to remember, and a couple of dramatic closure announcements…

But then we’re still here, soldiering on, still uncertain whether there’s a point to it, but grateful for tiny tokens of appreciation.

Such as this morning’s story: Chandan deemed it necessary to correct two spelling mistakes in a 2 year old Fun-math post on Weil and the Riemann hypothesis (also reposted on Neb here). Often there’s a story behind such sudden comments, and a quick check of MathOverflow revealed this answer and the comments following it.

I thank Ed Dean for linking to the Fun-post, Chandan for correcting the misspellings and Georges for the kind words. I agree with Georges that a cut&copy of a blogpost-quoted text does not require a link to that post (though it is always much appreciated). It is rewarding to see such old posts getting a second chance…

Above the Google Analytics graph of the visitors coming here via a mobile device (at most 5 on a good day…). Anticipating much more iPads around after tonights presents-session I’ve made NeB more accessible for iPods, iPhones, iPads and other mobile devices.

The first time you get here via your Mac-device of choice you’ll be given the option of saving NeB as an App. It has its own icon (lowest row middle, also the favicon of NeB) and flashy start-up screen.

Of course, the whole point trying to make NeB more readable for Mobile users you get an overview of the latest posts together with links to categories and tags and the number of comments. Sliding through you can read the post, optimized for the device.

I do hope you will use the two buttons at the end of each post, the first to share or save it and the second to leave a comment.

I wish you all a lot of mathematical (and other) fun in 2011 :: lieven.

3 Comments

Lists 2010 : StackExchange sites

Published December 27, 2010 by lievenlb

One of the trends of 2010 was the proliferation of StackExchange sites. I guess by now most of us visit MathOverflow along with the arXiv daily. But, there are plenty of other StackExchange sites around that may be of interest to the mathematics-community :

“Opening a StackExchange site is damn hard. First you have to find at least 60 people interested in the site. Then, when this limit is reached, a large amount of people (in the hundreds, but it really depends on the reputation of each participant) must commit and promise to create momentum for the site, adding questions and answers. When this amount is reached, the site is open and stays in closed beta for seven days. During this time, the committers have to enrich the site so that the public beta (which starts after the first seven days) gets enough hits and participants to show a self-sustained community.” (quote from ForTheScience’s StackExchange sites proliferation, this post also contains a list of StackExchange-projects in almost every corner of Life)

The site keeping you up to date with StackExchange proposals and their progress is area51. Perhaps, you want to commit to some of these proposals

or simply browse around area51 until you find the ideal community for you to belong to…

Leave a Comment