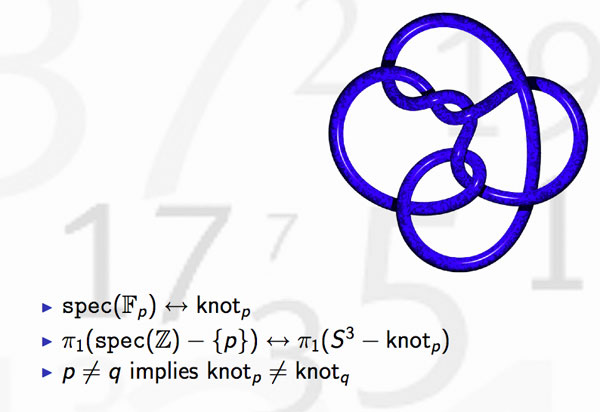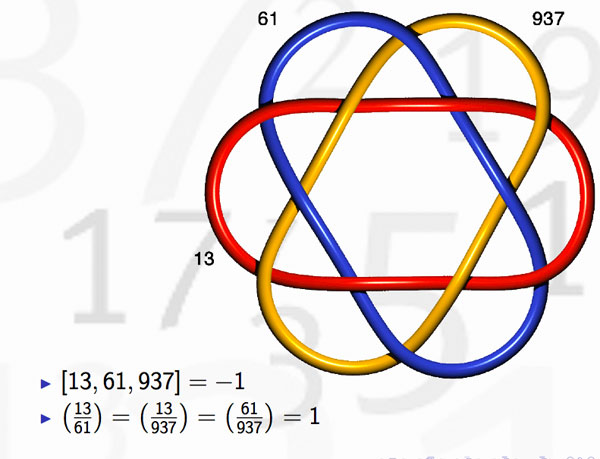Sometimes a MathOverflow question gets deleted before I can post a reply…
Yesterday (New-Year) PD1&2 were visiting, so I merely bookmarked the What is the knot associated to a prime?-topic, promising myself to reply to it this morning, only to find out that the page no longer exists.
From what I recall, the OP interpreted one of my slides of the April 1st-Alumni talk
as indicating that there might be a procedure to assign to a prime number a specific knot. Here’s the little I know about this :
Artin-Verdier duality in etale cohomology suggests that $Spec(\mathbb{Z}) $ is a 3-dimensional manifold, as Barry Mazur pointed out in this paper
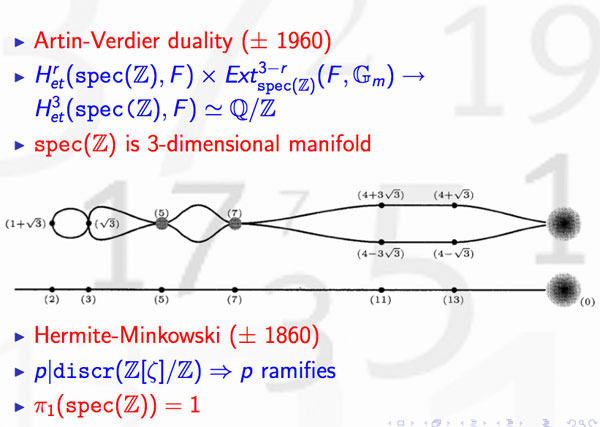
The theory of discriminants shows that there are no non-trivial global etale extensions of $Spec(\mathbb{Z}) $, whence its (algebraic) fundamental group should be trivial. By Poincare-Perelman this then implies that one should view $Spec(\mathbb{Z}) $ as the three-sphere $S^3 $. Note that there is no ambiguity in this direction. However, as there are other rings of integers in number fields having trivial fundamental group, the correspondence is not perfect.
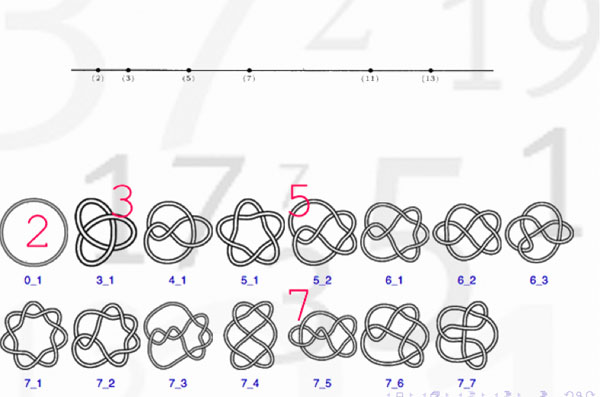
Okay, but then primes should correspond to certain submanifolds of $S^3 $ and as the algebraic fundamental group of $Spec(\mathbb{F}_p) $ is the profinite completion of $\mathbb{Z} $, the first option that comes to mind are circles

Hence, primes might be viewed as circles embedded in $S^3 $, that is, as knots! But which knots? Well, as far as I know, nobody has a procedure to assign a knot to a prime number, let alone one having p crossings. What is known, however, is that different primes must correspond to different knots
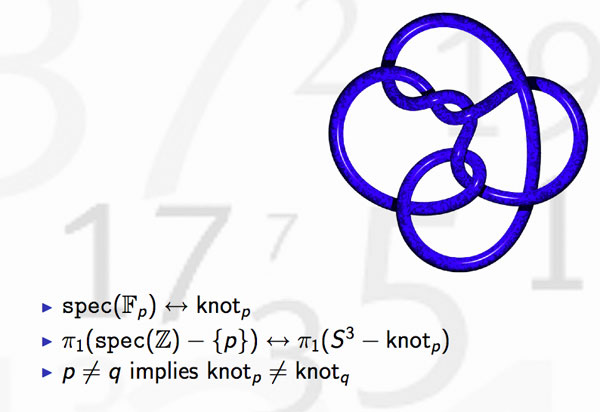
because the algebraic fundamental groups of $Spec(\mathbb{Z})- { p } $ differ for distinct primes. This was the statement I wanted to illustrate in the first slide.
But, the story goes a lot further. Knots may be linked and one can detect this by calculating the link-number, which is symmetric in the two knots. In number theory, the Legendre symbol, plays a similar role thanks to quadratic reciprocity
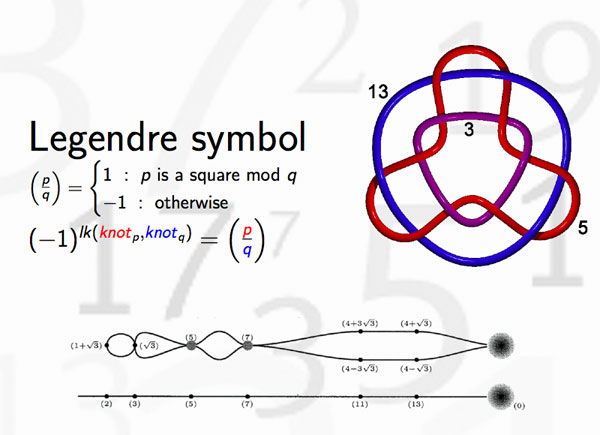
and hence we can view the Legendre symbol as indicating whether the knots corresponding to different primes are linked or not. Whereas it is natural in knot theory to investigate whether collections of 3, 4 or 27 knots are intricately linked (or not), few people would consider the problem whether one collection of 27 primes differs from another set of 27 primes worthy of investigation.
There’s one noteworthy exception, the Redei symbol which we can now view as giving information about the link-behavior of the knots associated to three different primes. For example, one can hunt for prime-triples whose knots link as the Borromean rings
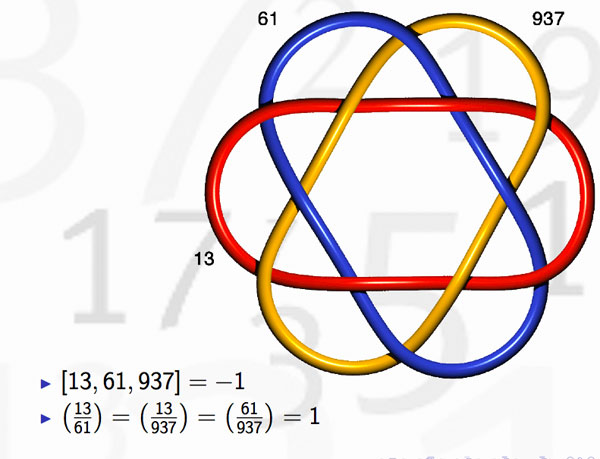
(note that the knots corresponding to the three primes are not the unknot but more complicated). Here’s where the story gets interesting : in number-theory one would like to discover ‘higher reciprocity laws’ (for collections of n prime numbers) by imitating higher-link invariants in knot-theory. This should be done by trying to correspond filtrations on the fundamental group of the knot-complement to that of the algebraic fundamental group of $Spec(\mathbb{Z})-{ p } $ This project is called arithmetic topology
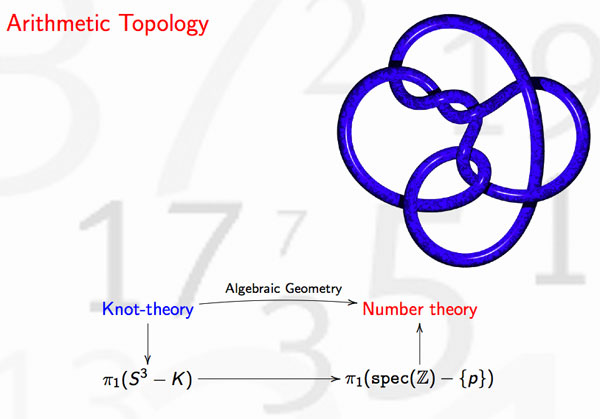
Perhaps I should make a pod- or vod-cast of that 20 minute talk, one day…